Numa escola secundária, relativamente aos alunos do 12

Proposta de Teste – Matemática A 11.º ano
Nome da Escola
Ano letivo 20
Nome do Aluno
Turma
- 20
N.º
Matemática A | 11.º ano
Data
Professor
-
- 20
GRUPO I




Os cinco itens deste grupo são de escolha múltipla. Em cada um deles, são indicadas
quatro opções, das quais só uma está correta.
Escreva na sua folha de respostas apenas o número de cada item e a letra
correspondente à opção que selecionar para responder a esse item.
Não apresente cálculos nem justificações.
Se apresentar mais do que uma opção, a resposta será classificada com zero pontos,
o mesmo acontecendo se a letra transcrita for ilegível.
1. Considere, fixado um referencial cartesiano do espaço, os pontos A  2, 7, 5  ,
B  7,7,  4  e C  2,10, 2  . A amplitude do ângulo BAC é igual a:
(A) 30º
(B) 60º
(C) 120º
(D) 150º
2. De duas funções f e g, de domínio IR, sabe-se que:

f é uma função ímpar e injetiva;

g é uma função par;

f  3   2 e g  3   2


Qual é o valor de f 1 g  3  ?
(A) 2
(B) – 2
(C) 3
(D) – 3
3. Considere, num referencial o.n. xOy, o gráfico de uma função f, de domínio IR, e os
pontos A  0,  3 e B 1,  1 . Sabe-se que a reta AB é tangente ao gráfico de f no
ponto de abcissa 1.
Então, pode-se afirmar que:
(A) f 1  5 e f  1  2
(C) f 1  1 e f  1 
1
2
(B) f  0   3 e f  1  2
(D) f 1  1 e f  1  2
4. Seja  un  a sucessão definida por recorrência do seguinte modo:
u1  100

un  un 1  2, se n  1
A soma dos 100 primeiros termos de  un  é igual a:
(A) 100
(B) – 100
(C) 0
(D) 19 900
1
Proposta de Teste – Matemática A 11.º ano
5. Considere, num referencial o.n. Oxyz, o plano  de equação x  y  2z  1 e a reta r
definida por x 
y 1
z.
3
Qual das afirmações seguintes é verdadeira?
(A) A reta r está contida no plano .
(B) A reta r é estritamente paralela ao plano .
(C) A reta r é concorrente e perpendicular ao plano .
(D) A reta r é concorrente e não perpendicular ao plano .
GRUPO II
Nas respostas aos itens deste grupo, apresente todos os cálculos que tiver de efetuar e
todas as justificações necessárias.
Atenção: quando, para um resultado, não é pedida a aproximação, apresente sempre o
valor exato.
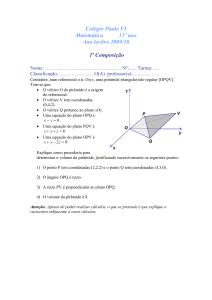
1. Considere o quadrado [ABCD] representado na figura 1. Os pontos P e Q pertencem
aos lados [AB] e [BC], respetivamente.
D
C
Q
A
P
B
Figura 1
Sabe-se ainda que:

PB  QC

PB 
1
AP
4
1.1. Prove que os vetores AQ e DP são perpendiculares.
1.2. Seja  amplitude do ângulo BPD.
Determine o valor exato de sin  2  .
1.3. Fixado um referencial ortonormado do plano, são conhecidas as coordenadas dos
 8 11
pontos A, Q e C: A  0,  4  , Q  ,  e C 1, 3  .
5 5 
1.3.1. Mostre que CQ  1 .
1.3.2. Determine as coordenadas do ponto B .
2
Proposta de Teste – Matemática A 11.º ano
2. Considere a função f, de domínio IR \ {1}, definida por f  x  
2.1. Resolva analiticamente a condição f  x  
x2
3.
x 1
3  2x
.
x 1
Apresente o conjunto-solução usando a notação de intervalo de números reais.
2.2. Considere os pontos A, B e C tais que:

A é o ponto de interseção das assíntotas do gráfico de f;

B e C são os pontos de interseção das assíntotas do gráfico de f com a
bissetriz dos quadrantes ímpares.
Determine a área do triângulo [ABC]
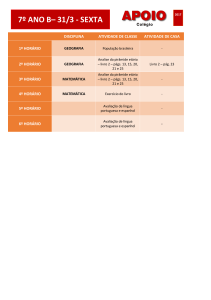
3. Na figura 2 está representada, em referencial o.n. Oxyz, uma pirâmide quadrangular
[OABCV] e uma reta r.
z
r
V
C
A
O
y
B
Figura 2
x
Sabe-se que:

a reta r é definida pelas equações x  y  9  z ;

o ponto V pertence à reta r e tem todas as coordenadas não negativas

o ponto A pertence ao eixo Ox e tem abcissa igual à do ponto V;

o ponto C pertence ao eixo Oy e tem ordenada igual à do ponto V;

o ponto B é a projeção ortogonal do ponto V no plano xOy.
3.1. Sendo x a abcissa do ponto V, mostre que o volume da pirâmide, em função de x, é
dado por V  x   3 x 2 
x3
, com x  0, 9 .
3
3.2. Utilizando a função derivada de V e recorrendo a métodos exclusivamente
analíticos, determine o volume máximo da pirâmide.
3.3. Determine o volume da pirâmide, sabendo que a reta r é perpendicular ao plano
AVC.
FIM
3
Proposta de Teste – Matemática A 11.º ano
COTAÇÕES
(5  10 pontos)
GRUPO I
50 pontos
GRUPO II
1.
65 pontos
1.1.
20 pontos
1.2.
15 pontos
1.3.
30 pontos
1.3.1.
10 pontos
1.3.2.
20 pontos
2.
35 pontos
2.1.
20 pontos
2.2.
15 pontos
3.
50 pontos
3.1.
15 pontos
3.2.
20 pontos
3.3.
15 pontos
Total
200 pontos
4