Aula 02

Mecânica I (FIS-14)
Prof. Dr. Ronaldo Rodrigues Pelá
Sala 2602A-1
Ramal 5785
[email protected]
www.ief.ita.br/~rrpela
Método de Estudo
●
Estudante é diferente de aluno
–
Etimologicamente: aluno significa “criança de
peito”, “lactante” ou “filho adotivo” (do lat.
alumnus, alumni, proveniente de alere, que
significa “alimentar, sustentar, nutrir, fazer
crescer”).
–
O termo aluno aponta, portanto, para a ideia de
alguém imaturo, que precisa ser alimentado na
boca e exige ainda muitos cuidados paternais ou
maternais
Método de Estudo
●
●
●
●
Método de estudo é algo pessoal
Planeje seu estudo: veja as matérias que precisa estudar, organize um
cronograma (o qual pode ser variável para cada semana, por exemplo)
Programe suas atividades extra-curriculares de modo a respeitar seus próprios
limites
No seu planejamento, reserve algum tempo para atividades que descansam
–
●
Dedique para cada disciplina o tempo que você precisa dedicar
–
●
Um erro muito comum é se estudar apenas o que se gosta: na verdade é preciso estudar
cada matéria de acordo com o que ela exige algumas vezes, você precisará dedicar mais
tempo a algumas matérias das quais não goste tanto
Periodicamente, revise seu método de estudo e veja o que está funcionando e o
que deve ser melhorado
–
●
esporte, leitura de livros, filmes, reuniões com amigos, etc.
Os resultados levam tempo para aparecer, tenha paciência para não desistir nas
primeiras diculdades
Peça conselho a outros professores ou a colegas mais experientes
Revisão
●
Algarismos significativos
–
0,333 => 3 alg. sign.
–
3,155 => 4 alg. sign.
–
3 => 1 alg. sign.
–
3,0 => 2 alg. sign.
–
30 => 2 alg. sign.
–
300 => 3 alg. sign.
–
3,010 => 4 alg. sign.
–
0,033 => 2 alg. sign.
–
0,030 => 2 alg. sign.
Revisão
●
Algarismos significativos
–
Algarismo significativo é diferente de casa decimal
–
Fazer os cálculos com a maior quantidade de
casas decimais possível
–
No final, ao dar a resposta, colocar com a
quantidade adequada de algarismos significativos
●
–
Regra do “mais pobre”
Arredondar sempre para o número mais próximo
●
Arredondar não é o mesmo que truncar
Revisão
●
●
Exemplo: um corpo de 3,00 kg está sujeito a
uma força de 10 N. Qual a aceleração deste
corpo? Qual o deslocamento do corpo após 3,00
s, considerando que o mesmo partiu do
repouso?
Solução:
–
Aceleração: a = F/m = 10/3,00 = 3,33333 m/s2
–
Considerando alg. sign.: a = 3,3 m/s2
–
Distância: d = at2/2 = (3,3333)*(3,00)2/2 = 15,000 m
–
Considerando alg. sign.: d = 15 m
Revisão
●
Escalar: qualquer quantidade física positiva ou
negativa que pode ser completamente
especificada por sua intensidade.
–
●
Exemplos: distância, comprimento, massa, tempo
Vetor: quantidade física que requer uma
intensidade e uma direção para sua completa
descrição
–
Esta é uma condição necessária, mas não
suficiente para descrever uma grandeza vetorial
–
Contra-exemplo: ângulo (rotação)
Revisão
●
●
Vetor
–
A soma precisa
satisfazer alguns
axiomas ...
–
Exemplos de vetores
“verdadeiros”: Força,
Deslocamento, Spin
Soma de vetores
–
Soma: componente a
componente
Revisão
●
●
Produto escalar
–
A = Ax x+Ayy+Azz
–
B = Bx x+Byy+Bzz
–
A.B = AxBx+AyBy+AzBz
Produto vetorial
Estática
●
Estática de uma partícula:
–
Equilíbrio = repouso ou movimento uniforme
–
Repouso = Equilíbrio estático
–
Movimento uniforme = Equilíbrio dinâmico
–
Condição necessária e sufiente para o equilíbrio
●
●
Força resultante = 0
Diagrama de corpo livre: melhor maneira de
“enxergar” as forças que atuam sobre uma
partícula
Estática
●
Exemplo: determine intensidade da força
desenvolvida em cada cabo, se a carga
suportada tem 40,0 kN
Estática
●
Modo trabalhoso
–
●
Coordenadas cartesianas e decomposição de vetores
Modo simples
–
Pela simetria: FB = FC. Componente vertical de FB e
FC é 20 kN cada.
–
FBz/FB = 8/sqrt(89). FB = 23,48494283 kN
–
Logo FB = FC = 23,6 kN
–
Com um pouco de geometria, segue
–
FA = 2*FB*3/sqrt(89)
–
Logo FA = 15,0kN
Estática
●
Estática de corpos rígidos
●
Momento (torque) de uma força
●
–
Quando uma força é aplicada a
um corpo, ela produzirá uma
tendência de rotação em torno de
um ponto que está na linha de
ação da força
–
Esta “tendência de rotação” é o
momento (ou torque) da força
Produto vetorial
Estática
●
Princípio da transmissibilidade
Estática
●
Momento binário
Estática
●
Força resultante equivalente
–
Substituir o ponto de ação de uma força
Estática
●
Força resultante
equivalente
–
Simplificar um sistema
de forças e momentos
Estática
●
Força resultante equivalente
–
Redução a um torsor
Eixo de parafuso
Estática
●
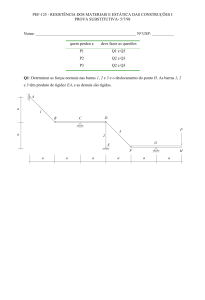
Exemplo: Substitua o sistema de forças e
momentos que agem sobre a viga por uma
força resultante equivalente e encontre onde a
linha de ação desta força intercepta a viga
(medindo a distância a partir do ponto O)
Estática
●
Solução:
–
Achar a força resultante
●
●
●
–
FRx = 4,80 kN
FRy = 2,40 kN
FR = 5,37 kN e θ = 26,6O
Igualar o momento da força FR ao momento
resultante
●
●
2,40d = -4*(1,5) - 15 - (8)(3/5)(0,5) + (8)(4/5)(4,5)
d = 2,25 m
Estática
●
Condições de equilíbrio do
corpo rígido
–
Força resultante nula
–
Momento resultante nulo
Estática
●
Reações de apoio: regra geral
–
Se um apoio impede a translação
numa certa direção, então uma
força é desenvolvida no corpo
nesta direção
–
Se a rotação é impedida, então
um momento de binário é exercido
sobre o corpo