2º Teste versãoA Técnico Lisboa Dep. Física 19/11/2014 2º Teste de

2º Teste de Electromagnetismo e Óptica 2014/11 1ºS versão A
Dep. Física
Cursos: MEAmbi+LEMat
Prof. Amilcar Praxedes
19/11/2014, 18h-19h
I Indução [10]
Um circuito rectangular, de lados
l1 e l2 é constituído por
N=4000 espiras de um fio muito fino de modo que a sua
espessura pode ser considerada desprezável face à dimensão
li .
Este circuito é obrigado a rodar em torno de um eixo horizontal
(eixo dos ZZ) com velocidade angular,


  (0  kt) ez (rad s-1).
O circuito encontra-se “mergulhado” num Campo de Indução

Magnética B , uniforme ( no espaço) e constante (no tempo).

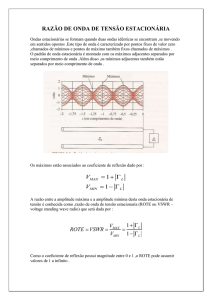
A figura apresenta esquematicamente, num dado instante, a posição relativa entre o vector n (normal ao plano do circuito) e

o Campo de Indução Magnética B .


Considere que no instante inicial o ângulo entre n e B é de nulo e que o sistema parte do repouso.
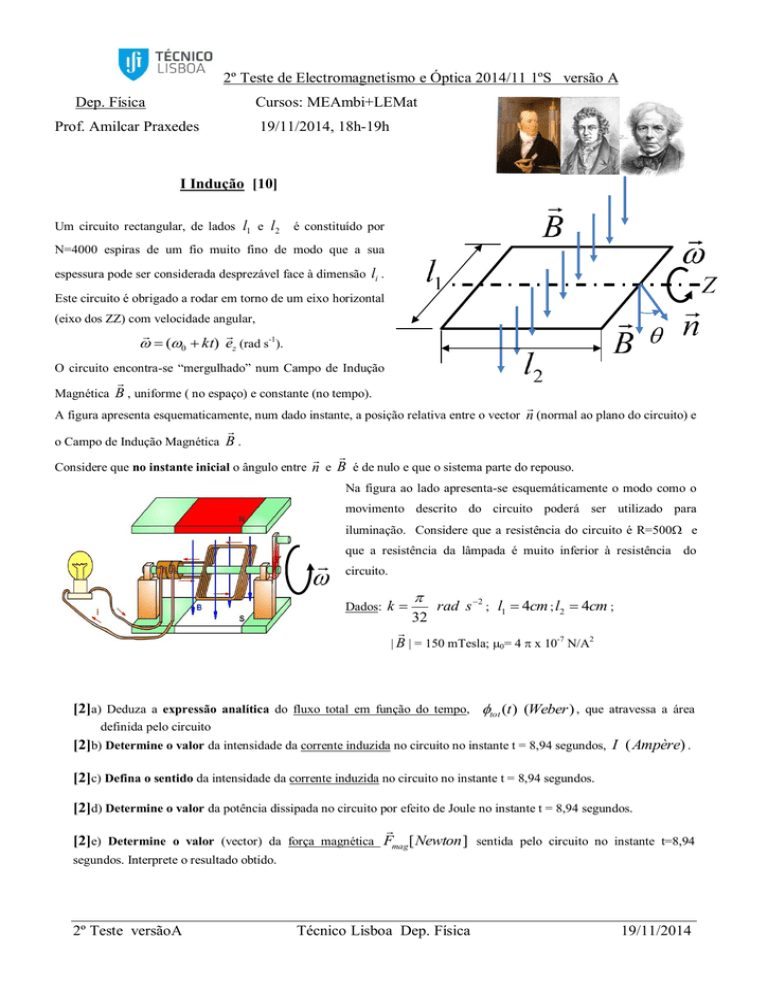
Na figura ao lado apresenta-se esquemáticamente o modo como o
movimento descrito do circuito poderá ser utilizado para
iluminação. Considere que a resistência do circuito é R=500 e
que a resistência da lâmpada é muito inferior à resistência do
circuito.
Dados: k 


32
rad s 2 ; l1  4cm ; l2  4cm ;
| B | = 150 mTesla; 0= 4 x 10-7 N/A2
[2]a) Deduza a expressão analítica do fluxo total em função do tempo, tot (t ) (Weber ) , que atravessa a área
definida pelo circuito
[2]b) Determine o valor da intensidade da corrente induzida no circuito no instante t = 8,94 segundos, I (Ampère) .
[2]c) Defina o sentido da intensidade da corrente induzida no circuito no instante t = 8,94 segundos.
[2]d) Determine o valor da potência dissipada no circuito por efeito de Joule no instante t = 8,94 segundos.

[2]e) Determine o valor (vector) da força magnética Fmag [Newton ] sentida pelo circuito no instante t=8,94
segundos. Interprete o resultado obtido.
2º Teste versãoA
Técnico Lisboa Dep. Física
19/11/2014
II- Circuitos em AC [5]
A fonte de tensão: V  V0 cos t está
directamente aplicada a um circuito série
V 
R
X
VX
resistência R  ? k
e outro elemento
de impedância X  i 3 k .
Temos que
é de f
V0  311 Volt e a frequência
 50 kHertz .
[2]a) Sabendo que os voltímetros VR e VX
indicam precisamente o mesmo valor
determine o valor do módulo da impedância
do circuito série-RX: |Z|(.
VR
[2]b) Determine o valor da desfazagem da corrente que percorre o circuito relativamente à tensão da fonte.
[1]c) Represente VR eff (Volt ) , VXeff (Volt ) e Veff (Volt ) num diagram de phasors para t > 0.
III- Transformadores [5]
Um transformador foi construido com N1=1000 espiras e N2=5000 espiras.
[2]a) O secundário foi “carregado” com uma impedância X.
Sabendo que o valor com esta impedância é “vista” do primário é:
X*=(1000 + i 2000) 
determine o valor da impedância X.
Ou, de outro modo, sabendo que o valor com que a fonte aplicada no primário “sente” a impedância X, é de:
X*=(1000 + i 2000) 
determine o valor da impedância X.


[2]b) A resistência R= 50 está montada em série com a fonte que foi aplicada no primário.
Se a tensão da fonte for VF  V0 cos t em que V0  50 Volt e f  50 Hz , qual o valor da
intensidade efectiva da corrente que está a percorrer o primário,

[1]c) Qual a desfasagem da corrente
2º Teste versãoA
I1eff ?
I1 no primário em relação à tensão da fonte, VF ?
Técnico Lisboa Dep. Física
19/11/2014