A ponte Wheatstone

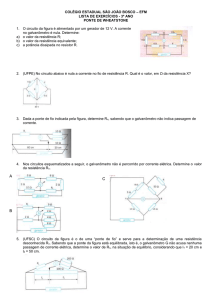
Exp. 12 - Estudo da ponte de Wheatstone
Introdução
12.1
Um problema comum que se encontra na vida diária é a determinação da resistência de um resistor. Lembremos que a
resistência elétrica é uma característica dos bipolos lineares e, nesse tipo de bipolo vale a Lei de Ohm, ou seja, aplicando-se sobre ele
uma diferença de potencial V aparece uma corrente I tal que
R=
V
I
Equação 12-1
Evidentemente essa equação pode ser utilizada para a determinação da resistência do resistor. Entretanto para que a
resistência possa determinada com precisão é necessário que tanto V como I sejam determinados também com precisão, ou seja,
são necessários instrumentos de qualidade, nem sempre disponíveis.
Para contornar este problema foi desenvolvida uma técnica que permite determinar a resistência de um resistor a partir de
resistores padrões e/ou de medidas puramente geométricas. Essas técnicas baseiam-se num circuito particular denominado ponte e
que apresenta diversas variantes, a mais simples delas é a chamada Ponte de Wheatstone.
12.2
A ponte de wheatstone
O circuito apresentado abaixo é denominado Ponte de Wheatstone.
Figura 12-1
Observe a existência de um voltímetro entre os pontos A e B que indica a diferença de potencial entre esses pontos. Quando
essa diferença de potencial for nula, isto é, quando o potencial em A for igual ao potencial em B, dizemos que a ponte está equilibrada.
Admitido o equilíbrio, não há corrente através do voltímetro e podemos afirmar que as correntes nos resistores
mesma (ramo DAC) bem como as correntes nos resistores
figura acima.
Como no estado de equilíbrio
R1
e
R2
RP
e
R
éa
também são as mesmas (ramo DBC) conforme está indicado na
V A = VB deveremos ter:
VC − VA = VC − VB ou e R P ⋅ I a = R 1 ⋅ I b
VA − VD = VB − VD ou R ⋅ Ia = R 2 ⋅ I b
R P ⋅ Ia R1 ⋅ I b
=
R ⋅ Ia
R2 ⋅ Ib
R P R1
=
R
R2
Dividindo membro a membro estas duas equações:
ou
Equação 12-2
Esta última equação é denominada equação de equilíbrio da ponte. Sempre que os valores das resistências empregadas
obedecer a esta relação a ponte estará equilibrada, isto é o voltímetro indicará zero.
12.3
Medida de uma resistência utilizando a ponte
Suponhamos que montemos a ponte mostrada acima utilizando um resistor desconhecido R e ajustemos R P , R1 e R 2
de tal forma que a ponte entre no estado de equilíbrio, isto é, que o voltímetro indique zero. Nessa condição vale a Equação 12-2 que
permitirá conhecer a resistência desconhecida, desde que se conheça as resistências R P , R1 e R 2 , ou seja, teremos:
R=
R2
⋅RP
R1
Equação 12-3
R será determinada dependerá da precisão com
e R 2 , ou seja, são necessárias três resistências de precisão. Este problema é parcialmente
Embora esta técnica esteja correta, ela não é útil pois a precisão com que
que se conhece os valores de R P , R 1
resolvido com a técnica descrita abaixo.
12.4
A ponte de fio
A ponte de fio é uma variação da ponte de Wheatstone que reduz a exigência de três resistores de precisão para apenas
um.
R1 e R 2 , é substituído por um único fio, geralmente de NiCr, de
tal forma que R 1 e R 2 são determinados por um cursor deslizante no ponto B. Assim os valores de R 1 e R 2 são mudados,
variando-se os comprimentos do fio correspondentes, indicados por l1 e l 2 ,que podem ser medidos com uma simples régua.
Na ponte de fio acima descrita, o ramo DBC, que contém
Figura 12-2
Lembremos agora que a resistência de um condutor filiforme é dada por
(S
R = ρ⋅
l
.
S
Sendo o fio de secção uniforme
= c te ) e homogêneo ( ρ = c te ) podemos escrever para as resistências R1 e R 2 :
l
l
R1 = ρ ⋅ 1 e R 2 = ρ ⋅ 2
S
S
Substituindo na Equação 12-3:
l
ρ⋅ 2
S
R = RP ⋅
l
ρ⋅ 1
S
ou
l
R = RP ⋅ 2
l1
Equação 12-4
Observemos agora que a resistência desconhecida
R
pode ser determinada em função de uma resistência padrão
RP
e
das medidas de dois comprimentos l1 e l 2 os quais podem ser obtidos pela utilização de uma simples régua.
O circuito final da ponte de fio fica:
A análise da Equação 12-4 nos leva a concluir que a resistência padrão não pode assumir qualquer valor pois se esta for
muito diferente da resistência que será medida teremos uma ralação entre os comprimentos a medir muito grande o que dificultará suas
medidas
12.5
Objetivos da experiência:
O objetivo desta experiência é medir a resistência pela técnica da ponte de fio descrita acima, comparando-a com o valor
nominal da mesma, isto é, com aquele indicado pelo fabricante.
12.6
Procedimento experimental:
12.6.1.1 ( ) Monte o circuito abaixo, ajustando a fonte previamente para 5V. Nesse circuito
Rp
é a resistência tomada como padrão. Use uma década para atribuir a
ponte. Comece com
R p = 200000Ω
R p um
Rx
é a resistência a ser determinada e
valor conveniente para permitir o equilíbrio da
Use o fio mais fino da prancha recebida, que contém 4 fios.
12.6.1.2 ( ) Uma vez montado e conferida a montagem, apóie o cursor sobre o fio e observe movendo-o sobre o fio o voltímetro dará
indicações diferentes. Cuidado pois a tensão poderá ser positiva ou negativa, fazendo o ponteiro deslocar-se nos dois sentidos.
12.6.1.3 ( ) Procure encontrar a posição na qual o voltímetro indique zero (condição de equilíbrio da ponte). Se o cursos se deslocar
até um extremo do fio e não for alcançada a posição de equilíbrio significa que o valor de
Rp
não é conveniente. Reduza então
para um décimo de seu valor sucessivamente até obter o equilíbrio.
12.6.1.4 ( ) Uma vez que o voltímetro indique zero, isto é, que a ponte esteja equilibrada, meça os valores de I1 e
12.6.1.5 ( ) Lendo o valor de
Rp
da década, aplique então a Equação 12-4, calculando o valor da resistência
Rx .
12.6.1.6 ( ) Compare o valor calculado com o valor nominal indicado pelo fabricante através do código de cores.
12.6.1.7 ( ) Calcule o erro percentual, admitindo o valor nominal como verdadeiro.
12.6.1.8 ( ) Repita o procedimento com outros resistores.
12.7
Siga as instruções contidas no anexo correspondente.
Relatório
I2 .
Rp