Capítulo 2

Capítulo 2
Curvas Características de Bipolos
Neste capítulo são verificadas as condições de
validade da Lei de Ohm e analisado um método para
obter
a
curva
característica
de
um
bipolo,
particularmente para bipolos resistivos linear e nãolinear, bem como a obtenção do valor da sua
resistência elétrica.
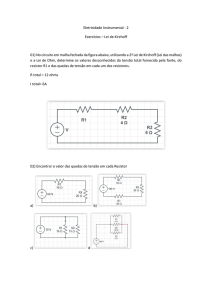
Exemplos de curvas características de bipolos
U
U
I
LINEAR
I
NÃO-LINEAR
1
CONCEITO DE RESISTÊNCIA
DIAGRAMA DE UM CIRCUITO ELÉTRICO COM FONTE C.C.
É VÁLIDA A SEGUINTE RELAÇÃO:
u(t)
i(t) =
R
R representa a resistência do resistor
2
LEI DE OHM
Em 1827, Georg Simon Ohm descobriu que, para
certos materiais, a relação entre a diferença de
potencial (U) aplicada entre dois pontos de um
condutor e a corrente (I) que flui entre estes dois
pontos, a uma dada temperatura, é constante.
Esta constante é a resistência (R) do condutor:
U
R =
I
Representação gráfica da Lei de Ohm
U
Bipolo Ôhmico
Resistor Linear
ou simplesmente Resistor,
é aquele cuja relação
tensão/corrente é
I
constante e, portanto,
satisfaz plenamente a
Lei de Ohm.
3
Obtenção de curvas características
Método do voltímetro e amperímetro
A
A
b
i
p
o
l
o
fonte CC
Ajustável
V
fonte CC
Ajustável
Circuito 1
b
i
p
o
l
o
V
Circuito 2
Analise:
Dado que um amperímetro tem resistência interna da ordem
de miliohms e um voltímetro tem resistência interna da
ordem de megaohms, para um bipolo com resistência
elevada (megaohms), qual destes circuitos é o mais
adequado para a obtenção da respectiva curva característica?
Justifique sem o uso de fórmulas ou equações.
4
Tolerância no valor do resistor
Os
resistores
são
usualmente
especificados
por
três
parâmetros:
valor nominal
/
tolerância
/
potência máxima dissipada
que são informados pelo fabricante no próprio resistor, seja
numericamente ou por código de cores.
Exemplo:
Se um resistor com valor nominal 1 kΩ, tem uma tolerância
de 5%, isto significa que sua resistência pode assumir
qualquer valor entre 950 e 1050 Ω (1 kΩ ± 5%).
Esta informação é importante, p.ex., para selecionar o fundo
de escala de um amperímetro a ser conectado em série com
o resistor.
5
Exemplo:
Resistor de 1 kΩ, 10 W e tolerância de 5%.
Para selecionar o fundo de escala do amperímetro, deve-se
calcular o valor da corrente que poderá circular neste resistor,
com base no menor valor possível da resistência, ou seja,
950 Ω. Assim:
I = P/R =
10
= 0 ,1026 A ou 102,6 mA
950
Selecione no amperímetro, o valor de fundo de escala
imediatamente acima do valor calculado.
6
Erro percentual ou relativo
É o erro, expresso em porcentagem, obtido em relação a um
valor de referência da grandeza, o qual pode ser o valor
nominal; o valor medido ou até mesmo um valor calculado.
E(%) =
VG − VR
VR
VG – valor da grandeza
× 100% VR – valor de referência
Exemplo:
Resistor 1 kΩ ± 5% é conectado a uma fonte c.c. cuja tensão
medida com voltímetro é de 100 V.
Se um amperímetro registra 97,6 mA, a resistência pode ser
calculada:
R=
100
= 1024,6 Ω
0,0976
Considerando como valor de referência o valor nominal 1000
Ω, o erro relativo é de:
E(%) =
R calc − R no min al
R no min al
x 100 % =
1024 ,6-1000
1000
x 100 % =
2 ,46 %
Portanto, o valor calculado apresenta um erro de 2,46% em
relação ao valor nominal, abaixo da tolerância (5%).
7
Exemplo:
O mesmo Resistor 1 kΩ ± 5% é conectado a um ohmímetro e
obtém-se 1024 Ω.
Considerando como valor de referência, a leitura do
ohmímetro, pode-se avaliar a precisão do valor nominal
informado pelo fabricante e nesse caso o erro relativo é de:
E(%) =
Rno min al − Rmedido
Rmedido
x 100 % =
1000-1024
1024
x 100 % =
2,34 %
Neste caso, o valor nominal apresenta um erro de 2,34% em
relação ao valor do ohmímetro, também abaixo da tolerância
(5%).
Vídeo:
Obtenção da Curva Característica de Bipolos - Procedimento Experimental.
http://www.youtube.com/watch?v=Um9k0YBoVxQ
8