Movimento Circular e Leis de Newton

Movimento Circular e Leis de Newton
Questão 1
d) será desacelerado.
A importância e a obrigatoriedade do uso do cinto de
e) apresentará um movimento circular uniforme.
segurança nos bancos dianteiros e traseiros dos veículos têm
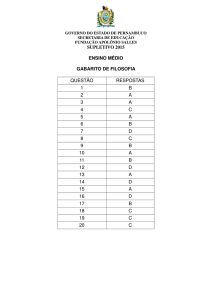
Gabarito:
sido bastante divulgadas pelos meios de comunicação. Há
B
grande negligência especialmente quanto ao uso dos cintos
traseiros. No entanto, existem registros de acidentes em que os
Questão 3
sobreviventes foram apenas os passageiros da frente, que
Analise as seguintes afirmativas:
estavam utilizando o cinto de segurança.
2
Quando necessário, use g = 10 m/s e π = 3.
I. Uma das três leis de Newton estabelece que uma força
sempre provoca variação na velocidade de um corpo.
a) Considere um carro com velocidade v = 72 km/h que, ao
colidir com um obstáculo, é freado com desaceleração
II. Uma das três leis de Newton estabelece que as forças
constante até parar completamente após Δt = 0,1 s. Calcule o
sempre aparecem aos pares.
módulo da força que o cinto de segurança exerce sobre um
passageiro com massa m = 70 kg durante a colisão para
III. Uma das três leis da termodinâmica estabelece que, em uma
mantê-lo preso no banco até a parada completa do veículo.
mudança de estado de um gás ideal, calor pode ser
integralmente convertido em trabalho.
b) Um passageiro sem o cinto de segurança pode sofrer um
impacto equivalente ao causado por uma queda de um edifício
IV. Uma das três leis da termodinâmica estabelece que uma
de vários andares. Considere que, para uma colisão como a
máquina de Carnot pode ter rendimento de 100%.
descrita, a energia mecânica associada ao impacto vale E = 12
kJ. Calcule a altura de queda de uma pessoa de massa m = 60
Dessas afirmativas, estão corretas
kg, inicialmente em repouso, que tem essa mesma quantidade
de energia em forma de energia cinética no momento da
01) I e II.
colisão com o solo.
02) II e III.
Gabarito:
04) III e IV.
(Resolução oficial)
08) IV e I.
a) O módulo da desaceleração do carro na colisão é
16) II e IV.
Gabarito:
.
02
A intensidade força do cinto pode ser calculada por
.
b)
Questão 4
Dois móveis, A e B, percorrem uma pista circular em
movimento uniforme. Os dois móveis partiram do mesmo
ponto e no mesmo sentido com as velocidades de 1,5 rad/s e
3,0 rad/s, respectivamente; o móvel B, porém, partiu 4
segundos
após
o
A.
Calcule o intervalo de tempo decorrido, após a partida de A, no
Questão 2
qual o móvel B alcançou o móvel A pela primeira vez.
A primeira Lei de Newton afirma que, se a soma de todas as
Gabarito:
forças atuando sobre o corpo é zero, o mesmo
a) terá um movimento uniformemente variado.
b) apresentará velocidade constante.
c) apresentará velocidade constante em módulo, mas sua
direção pode ser alterada.
Questão 5
Gabarito:
Dois projéteis, um de massa M e outro de massa m (M > m),
D
são lançados simultaneamente, com a mesma velocidade
0
, formando o mesmo ângulo θ com a horizontal.
Considerando que sobre eles atua constantemente a mesma
força resistiva
(figura), paralela à superfície horizontal,
Questão 7
Num velódromo, a pista apresenta uma inclinação
com a
horizontal num trecho em curva de raio R. Um ciclista com
velocidade escalar v faz uma curva horizontal com as mãos
soltas e sem contar com o atrito entre os pneus e a pista. A
podemos afirmar corretamente que
aceleração local da gravidade é g.
Nessas condições,
a)
01) o projétil de massa M tem maior alcance que o projétil de
massa
m.
02) a altura máxima atingida pelo projétil de massa M é menor
que a altura máxima atingida pelo projétil de massa m.
04) o módulo da força resultante que atua sobre o projétil de
massa M é maior que o módulo da força resultante que atua
sobre o projétil de massa m.
08) o projétil de massa M atinge o solo antes que o projétil de
.
b)
.
c)
.
d)
e)
.
.
Gabarito:
A
Questão 8
O gráfico a seguir representa uma relação entre a força
gravitacional F e a massa m de um objeto próximo à superfície
da
massa m o faça.
16) o módulo da aceleração do projétil de massa M é maior
que o módulo da aceleração do projétil de massa m.
Gabarito:
05
Questão 6
João e Maria empurram juntos, na direção horizontal e mesmo
sentido, uma caixa de massa m = 100 kg. A força exercida por
Maria na caixa é de 35 N. A aceleração imprimida à caixa é de 1
2
m/s . Desprezando o atrito entre o fundo da caixa e o chão,
pode-se dizer que a força exercida por João na caixa, em
Newtons, é:
a) 35.
b) 45.
c) 55.
d) 65.
e) 75.
O coeficiente angular da reta fornece
A) a aceleração da gravidade.
B) a constante universal da gravitação.
C) o momento do objeto.
D) o peso do objeto.
E) o torque.
Gabarito:
Terra.
A
Considere
Questão 9
a) 500 N.
Os três blocos A, B e C da figura a seguir se movem juntos sob
b) 1.000 N.
a ação da força
paralela à superfície horizontal. A força de
atrito entre a superfície horizontal e o bloco C é nula.
Desprezando a resistência do ar, assinale o que for correto.
g
=
10
m/s
2
e
ρágua
=
1.000
3
kg/m .
c) 5.000 N.
d) 10.000 N.
e) 30.000 N.
Gabarito:
C
Questão 12
Um garoto de 24 kg vê um vendedor de bexigas infladas com
gás hélio e pede à mãe 10 delas. A mãe compra apenas uma,
alegando que, se lhe desse todas, o menino seria erguido do
solo por elas. Inconformado com a justificativa, o menino
queixa-se à sua irmã, que no momento estudava empuxo,
perguntando-lhe qual seria o número máximo daquelas
bexigas que ele poderia segurar no solo. Considerando o
volume médio de cada bexiga, 2 litros, estime o número
01) Sobre o bloco A, atua uma força de atrito no mesmo
sentido da força
.
3
litro = 10 m e despreze as massas do gás e das bexigas.
Gabarito:
Se o valor do empuxo total for igual ao peso do garoto, ele
.
04) Sobre o bloco C, não atua força de atrito alguma.
08) A resultante das forças que atua no sistema formado pelos
três blocos é
3
cálculos, considere a massa específica do ar igual a 1,2 kg/m , 1
–3
02) Sobre o bloco B, atua uma força de atrito em sentido
contrário à força
mínimo de bexigas necessário para levantar o garoto. Em seus
terá sobre si uma resultante nula. Qualquer impulso que ele,
sem querer, der no solo, provocará uma reação que o colocará
em movimento, o qual se perpetuará em MRU, estando
novamente
sob
Então
se
resultante
nula
daí
para
frente.
.
16) A resultante das forças que atua nos blocos A e B é nula.
Gabarito:
Dessa forma,
11
em
,e
módulo
, mas este empuxo se
deve a várias bexigas, então será
Questão 10
Um automóvel, com rodas de 80 cm de diâmetro, viaja a 100
km/h sem derrapar. Logo, o módulo da velocidade angular das
Então:
suas rodas é aproximadamente
ou
A) 69,5 graus/s.
Em
B) 69,5 rev/s.
O valor de n será: n = 10.000 bexigas.
valores:
C) 69,5 m/s.
D) 69,5 rad/s.
Questão 13
Gabarito:
Uma bicicleta de marchas tem três engrenagens na coroa, que
D
giram com o pedal, e seis engrenagens no pinhão, que giram
com a roda traseira. Observe a bicicleta abaixo e as tabelas que
apresentam os números de dentes de cada engrenagem, todos
Questão 11
Um balão de ar, totalmente submerso, de massa m = 500 kg e
3
volume V = 1,00 m está amarrado a uma pedra de peso
30.000 N, no fundo de um lago. Calcule a tensão na corda que
amarra o balão à pedra.
de igual tamanho.
π = 3, a velocidade de translação na extremidade deste
ponteiro é:
Gabarito:
A
Questão 15
Dois discos, de raios RA e RB, giram com velocidades angulares
constantes acoplados ao mesmo eixo, como indicado na
Cada marcha é uma ligação, feita pela corrente, entre uma
engrenagem da coroa e uma do pinhão.
Suponha que uma das marchas foi selecionada para a bicicleta
atingir a maior velocidade possível.
Nessa marcha, a velocidade angular da roda traseira é WR e a
da coroa é WC .
figura.
A razão
equivale a:
Sabendo-se que RB = 3 RA, é CORRETO afirmar que a razão
entre as velocidades angulares dos discos A e B
(A)
(B)
(C)
(D)
e a
razão entre as velocidades lineares dos seus pontos periféricos
são,
respectivamente:
a)
1
e
1.
b)
3
e
3.
c)
1
Gabarito:
A
Questão 14
O ponteiro dos minutos de um relógio tem 1 cm. Supondo que
o movimento deste ponteiro é contínuo e que
(A) 0,1 cm/min.
(B) 0,2 cm/min.
(C) 0,3 cm/min.
(D) 0,4 cm/min.
(E) 0,5 cm/min.
d)
e 3.
Gabarito:
C
e
.