2ª Lei, Entropia e Formalismo Termodinâmico

Termodinâmica
Ano Lectivo 2002/03
2ª LEI, ENTROPIA E FORMALISMO TERMODINÂMICO
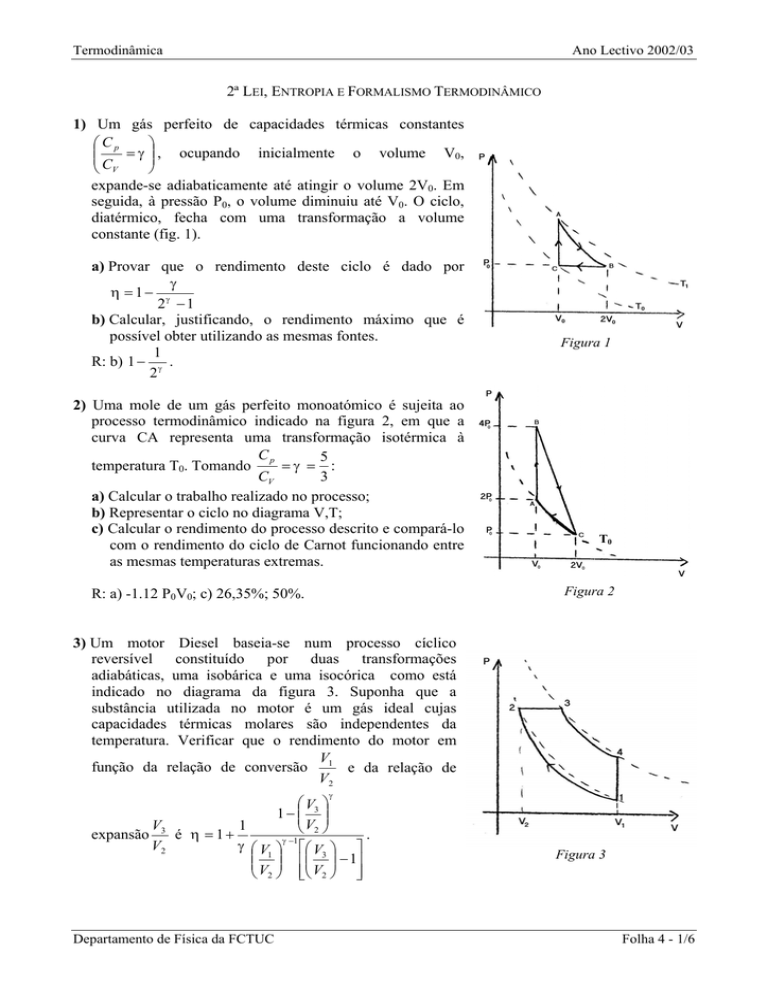
1) Um gás perfeito de capacidades térmicas constantes
 Cp


= γ  , ocupando inicialmente o volume V0,
 CV

expande-se adiabaticamente até atingir o volume 2V0. Em
seguida, à pressão P0, o volume diminuiu até V0. O ciclo,
diatérmico, fecha com uma transformação a volume
constante (fig. 1).
a) Provar que o rendimento deste ciclo é dado por
γ
η = 1− γ
2 −1
b) Calcular, justificando, o rendimento máximo que é
possível obter utilizando as mesmas fontes.
1
R: b) 1 − γ .
2
2) Uma mole de um gás perfeito monoatómico é sujeita ao
processo termodinâmico indicado na figura 2, em que a
curva CA representa uma transformação isotérmica à
Cp
5
temperatura T0. Tomando
=γ = :
CV
3
a) Calcular o trabalho realizado no processo;
b) Representar o ciclo no diagrama V,T;
c) Calcular o rendimento do processo descrito e compará-lo
com o rendimento do ciclo de Carnot funcionando entre
as mesmas temperaturas extremas.
Figura 1
T0
Figura 2
R: a) -1.12 P0V0; c) 26,35%; 50%.
3) Um motor Diesel baseia-se num processo cíclico
reversível constituído por duas transformações
adiabáticas, uma isobárica e uma isocórica como está
indicado no diagrama da figura 3. Suponha que a
substância utilizada no motor é um gás ideal cujas
capacidades térmicas molares são independentes da
temperatura. Verificar que o rendimento do motor em
V
função da relação de conversão 1 e da relação de
V2
γ
V 
1 −  3 
V
1
 V2 
expansão 3 é η = 1 +
.
γ −1
V2
γ  V   V  
 1   3  − 1
 V2   V2  
Departamento de Física da FCTUC
Figura 3
Folha 4 - 1/6
Termodinâmica
Ano Lectivo 2002/03
4) Determinar a variação da entropia de um gás perfeito nos seguintes tipos de transformações:
a) isotérmica, quando o volume varia de V0 para V1;
b) isobárica, quando a temperatura varia de T0 para T1;
c) isocórica, quando a temperatura varia de T0 para T1;
d) adiabática.
R: a) R ln (V1/V0); b) n CP ln (T1/T0); n CV ln (T1/T0); 0.
5) Um sistema é submetido à transformação representada no
diagrama entrópico da figura 4 pelo segmento de recta AB.
Determinar a quantidade de calor trocada na interacção com o
exterior.
R: (T1+T2)(S2-S1)/2.
6) A entropia de certa substância incompressível e não dilatável é
1
dada por S (T ) = A ln T02 + T 2 , em que T0 e A são constantes.
2
Mostrar que a quantidade de calor que é necessário fornecer à
substância
a
aquecer
desde
o
zero
absoluto
até
'
T
T  
u 
'
Q(T ) = AT0  − arctg  . (arc.tg u ) =

T0  
1+ u 2 
 T0
(
Figura 4
)
T
é
dada
por
7) Um gás perfeito de capacidade térmica a volume constante CV, encontra-se num estado inicial
definido por (V1,T1) e sofre uma transformação isotérmica reversível até atingir um volume
duplo do inicial; em seguida, uma expansão adiabática leva o gás até um volume 3V1; o ciclo
termina com uma transformação representável num diagrama (S,T) por um segmento de recta.
a) Representar o ciclo no diagrama S,T;
b) Determinar a temperatura correspondente ao estado final da transformação adiabática;
R
1  2 CV 
c) Provar que o rendimento do ciclo é
1−
, em que R é a constante dos gases

2  3

perfeitos.
2
R: b) T1  
3
γ −1
.
8) Calcular o rendimento do seguinte ciclo realizado
reversivelmente por um gás perfeito (fig. 5):
a) Compressão isotérmica à temperatura T0, desde a
pressão P0 até à pressão P1;
b) Transformação isobárica desde a temperatura T0 até que
a entropia adquira o valor primitivo S0;
c) Expansão adiabática até ao estado primitivo.
P
ln 1
P0
γ −1
.
R: 1 −
γ −1
γ
 P1  γ
  − 1
 P0 
Figura 5
9) Juntam-se dois corpos A e B, de massas mA e mB e capacidades térmicas mássicas a pressão
constante cA e cB, num recipiente isolado. Inicialmente as suas temperaturas são TAi e TBi.
Departamento de Física da FCTUC
Folha 4 - 2/6
Termodinâmica
Ano Lectivo 2002/03
Demonstrar, utilizando o 1º e 2º Princípios, que a temperatura final dos dois corpos é a mesma
TAf = TBf.
10) Calcular a variação de entropia do sistema formado por 1 kg de água a 27 ºC e 2 kg de gelo
fundente quando a água líquida e o gelo se põem em contacto dentro de um recipiente
adiabático. O calor de fusão do gelo é lfus = 334,4 J/g e a capacidade térmica mássica da água é
ca = 4,18 J/(gK). Qual é o aumento de entropia se se tiverem 0,2 kg de gelo em vez de 2 kg?
R: 22.24 JK-1; 17.14 JK-1.
11) Um sistema, com capacidade térmica CP, é aquecido a pressão constante de T1 até T2 por
contacto térmico com um certo número (tão grande quanto se queira) de fontes de calor, a
temperaturas entre T1 e T2. O aquecimento é reversível. A seguir, o sistema arrefece até T1,
mediante contacto térmico com uma só fonte à temperatura T1. Calcular as variações de
entropia, no aquecimento e no arrefecimento, do sistema, das fontes e do universo.
T 
T 
T 
R: Aquec.– Sistema: C P ln 2  ; Fonte: − C P ln 2  . Arref.– Sistema: − C P ln 2  ; Fonte:
 T1 
 T1 
 T1 
−
C P (T1 − T2 )
T1
12) Demonstrar que na expansão livre de um gás (não necessariamente perfeito) à temperatura T e
em contacto com uma fonte a essa temperatura, o aumento de entropia do universo é tal que
Vf
T∆SU = −WT = ∫ PdV ,
Vi
com WT o trabalho reversível e isotérmico entre os mesmos estados inicial e final (Vi e Vf são
os volumes inicial e final).
13) Tem-se 1 mol de um gás perfeito, de capacidade térmica a volume constante CV = 0,01 T (J/K)
em equilíbrio, a 200 K, com uma fonte a essa temperatura.
a) Qual é o trabalho mínimo que se deve realizar para elevar a temperatura do gás até 220 K se
o seu volume permanecer constante?
b) Qual é esse trabalho se, em vez do volume, a pressão for constante?
R: a) 2 J; b) 9,9 J
14) A partir da Equação Fundamental proposta por Gibbs para os gases perfeitos considerados
como sistemas fechados,
V
U = U (V , S ) = U 0 
 V0



− nR
CV
 S − S0
exp
 CV

 ,

sendo n o número de moles, e U0, V0, S0, CV = ncV e R constantes, extraia as equações de estado
térmica, energética e entrópica correspondentes.
nRT

 P = P(V , T ) = V ; U = U (V,T ) = CV T ;

nR


R: 
C
V
S = S (T , V ) = CV ln T + nR ln V + S 0 + CV ln  CV  1  
 U 0  V0  




Departamento de Física da FCTUC
Folha 4 - 3/6
Termodinâmica
Ano Lectivo 2002/03
15) A partir de dU = TdS − PdV , utilizando os Teoremas de Schwartz e da Reciprocidade e a
Regra da Derivação em Cadeia, deduza as Relações de Maxwell.
16) A partir de dU = TdS − PdV e utilizando uma das Relações de Maxwell deduza a equação
 ∂P 
 ∂U 
 −P.

 = T
 ∂T V
 ∂V  T
17) Determine a relação entre T e V num processo adiabático reversível para um gás de equação de
estado PV = nRT , CV = ncV , R e cV constantes. Que acontece à temperatura se o gás se
expandir? E se se tratar de uma expansão adiabática livre?
R: TV γ −1 = C te ; diminui; mantém-se constante.
18) Determine a relação entre T e P num processo adiabático reversível para um gás de equação de
estado PV = nRT , CV = ncV , R e cV constantes.
R: TP (1−γ ) γ = C te .
19) Suponha que um gás de van der Waals é utilizado numa máquina térmica que realiza um ciclo
de Carnot. Partindo da equação térmica

n2a 
 P + 2 (V − nb ) = nRT ,
V 

admitindo que CV é constante e utilizando o formalismo termodinâmico, determine:
a) as equações energética e entrópica características deste tipo de gás;
b) a variação da energia interna, da entropia, o calor trocado e o trabalho realizado no processo
isotérmico à temperatura T1 da fonte quente, variando o volume de V1 para V2;
c) a variação da energia interna, da entropia, o calor trocado e o trabalho realizado no processo
adiabático, quando a temperatura varia de T1 para T2 e o volume de V2 para V3;
d) a variação da energia interna, da entropia, o calor trocado e o trabalho realizado no processo
isotérmico à temperatura T2 da fonte fria, variando o volume de V3 para V4;
e) a variação da energia interna, da entropia, o calor trocado e o trabalho realizado no processo
adiabático, quando a temperatura varia de T2 para T1 e o volume de V4 para V1;
f) o rendimento do ciclo, verificando que se trata, de facto, do rendimento esperado para uma
máquina de Carnot.
n2a
n2a n2a
R: a) U = U 0 + CV T −
; S = S 0 + CV ln T + nR ln (V − nb ) ; b) ∆U = −
+
;
V2
V1
V
 V − nb 
 ; Q = T1∆S ; W = ∆U − Q ; c) Q = ∆S = 0 ;
∆S = nR ln 2
V
−
nb
 1

1 1
 V − nb 
n2a n2a
 ;
W = ∆U = CV (T2 − T1 ) − n 2 a −  ; d) ∆U = −
+
; ∆S = nR ln 4
V4
V3
 V3 V2 
 V3 − nb 
1 1
Q = T2 ∆S ; W = ∆U − Q ; e) Q = ∆S = 0 ; W = ∆U = CV (T1 − T2 ) − n 2 a − 
 V1 V4 
20) Certo autor afirmou que um sólido obedece à equação de estado térmica V = V0 − aP + bT ,
onde V0, a e b são constantes, e que obedece à equação de estado energética U = cT − bPT ,
com c constante. Demonstre que esta afirmação está errada pois as duas equações não podem
descrever a mesma substância.
Departamento de Física da FCTUC
Folha 4 - 4/6
Termodinâmica
Ano Lectivo 2002/03
21) Utilizando o ciclo de Mayer representado na figura
6 (três isotérmicas a temperaturas que diferem
infinitesimalmente, entre as quais tem lugar um
ciclo com um processo isocórico, um processo
isobárico e uma expansão livre), e o carácter de
função de estado da entropia, determine a variação
entrópica de cada processo e obtenha a Relação de
Mayer generalizada.
Figura 6
CV
C
C
 ∂P   ∂V 
dTb ; dS bc = P (− dTa − dTb ) ; dS ca = V dTa + 
 
 (dTa + dTb ) ;
T
T
T
 ∂T V  ∂T  P
TVα 2
C P − CV =
κT
R: dS ab =
22) Uma mole de um gás de equação de estado P(V − b ) = aT , onde a e b são constantes, e cuja
capacidade térmica a volume constante é CV = cT 2 , com c constante, realiza o seguinte ciclo:
partindo do estado inicial (V1, P1) ocorre um processo isocórico até ao valor superior de pressão
P2; segue-se um processo de expansão adiabática reversível até ao volume V2; novo processo
isocórico leva o sistema até uma pressão tal que um processo isotérmico o devolve, finalmente,
ao estado inicial.
a) Representar qualitativamente o ciclo em diagramas VP e ST.
b) Obter a condição que deve ser satisfeita pela temperatura T3 no final do processo adiabático.
c) Obter os trabalhos realizados e os calores trocados em cada um dos processos do ciclo.
R: b) T3 = T22 +
2a  V2 − b 

ln
c  V3 − b 
23) Um gás de equação de estado P(V − nσ ) = nRT e capacidade térmica a volume constante
CV = ncV , onde σ, R e cV são constantes, realiza o seguinte ciclo: a partir do estado inicial (T1,
V1) sofre um processo de expansão isotérmica reversível até alcançar o volume V2; a seguir, e a
volume constante, o gás arrefece até à temperatura T2 em contacto com uma só fonte de calor
à temperatura T2; realiza depois um outro processo de compressão isotérmica reversível até
alcançar o volume V1; finalmente, um processo isocórico em que o gás aquece até à
temperatura T1 em contacto com uma só fonte a essa temperatura devolve o sistema ao seu
estado inicial.
a) Representar qualitativamente este ciclo nos diagramas VP e ST.
b) Calcular o rendimento do ciclo.
c) Calcular a variação da entropia do universo no ciclo.
 V − nσ 

nR(T1 − T2 )ln 2
V1 − nσ 
nc (T − T ) nc (T − T )

R: b) η =
; c) ∆SU = V 1 2 − V 1 2
T2
T1
 V − nσ 
 + ncV (T1 − T2 )
nRT1 ln 2
 V1 − nσ 
Departamento de Física da FCTUC
Folha 4 - 5/6
Termodinâmica
Ano Lectivo 2002/03
24) Um pedaço de cobre de 5000 kg é aquecido, reversível e isobaricamente, de 800K até 1000K, à
pressão constante de 107 Pa. O coeficiente de dilatação do cobre no domínio de temperaturas
em causa é α = 31,5x10-6 K-1, o coeficiente de compressibilidade isotérmica é κT = 7,21x10-12
Pa-1 e a capacidade térmica mássica a volume constante é cV = 254 J.kg-1K-1. Consideram-se
estes valores constantes ao longo do processo. A massa volúmica do cobre à temperatura e
pressão iniciais é ρ = 8,930166x103 kg.m-3 e a 800K e 0Pa é ρ = 8,93000x103 kg.m-3. Calcular:
a) As variações da energia interna e da entropia durante o aquecimento.
b) A variação de volume do cobre, submetendo-o à mesma variação de temperatura mas
comprimindo-o de forma reversível e adiabática.
c) A variação de temperatura do cobre se, nas condições iniciais, a expansão pudesse ser
considerada livre e adiabática.
R: a) ∆U = 4.4 x1011 J ; ∆S = 4.9 x10 9 JK -1 ; b) –6.5x10-2 m3; c) Praticamente não varia.
25) Dois corpos incompressíveis e não dilatáveis, dotados de capacidades térmicas C iguais,
encontram-se à temperatura T1 e T2, respectivamente. Considerando uma transferência
reversível de calor de um corpo para o outro (através de ciclos de Carnot infinitesimais) até se
atingir igualdade de temperaturas, mostrar que a temperatura final dos corpos é dada por
T f = (T1T2 )
1
2
e que o trabalho realizado pelo agente auxiliar é W = C (T1 + T2 ) − 2C (T1T2 ) 2 . O
1
sistema constituído pelos dois corpos e pela máquina térmica que realiza os ciclos de Carnot
está isolado do exterior.
26) Duas garrafas contêm o mesmo gás de massa molecular M à temperatura T K. Os volumes das
garrafas são V1 e V2 e as pressões a que se encontra o gás são P1 e P2, respectivamente.
Supondo que o gás se comporta como um gás perfeito, se não se realizar trabalho exterior sobre
o gás e se as garrafas estão termicamente isoladas, demonstre que, ao pôr em comunicação as
m1 + m2
1 
R  m1 p 2 + m2 p1 

,
duas garrafas, a variação de entropia é dada por ∆S =
ln 
M  m1 + m2 
p1m2 p 2m1 


onde R é a constante dos gases perfeitos e m1 e m2 são as massas de gás contidas nas garrafas.
27) Um cilindro vedado em ambas as extremidades e dotado de paredes isoladoras é dividido por
meio de um êmbolo em duas partes iguais cada uma das quais contendo 1 mole de um gás
perfeito de capacidade térmica a volume constante CV = cV. Os volumes das duas partes do
cilindro eram inicialmente iguais a V1 e V2 mas a temperatura tinha o mesmo valor T K em
todo o volume. O êmbolo foi lentamente deslocado até à posição média. Tornou-se assim
possível o estabelecimento do equilíbrio térmico através do êmbolo que era condutor. No
entanto, a entropia total permanece constante visto que as paredes do cilindro são isoladoras.






2
Mostre que a temperatura final é dada por T f = T 

 V2 + V1 
 V
V2 
 1
Departamento de Física da FCTUC
R
CV
.
Folha 4 - 6/6