4- Cálculo Integral emℜ 4.1 Definição e interpretação geométrica de

Análise Matemática I - Ano Lectivo 2006/2007
4-
Cálculo Integral em ℜ
4.1 Definição e interpretação geométrica de integral definido.
Somas de Darboux.
Def.4.1-
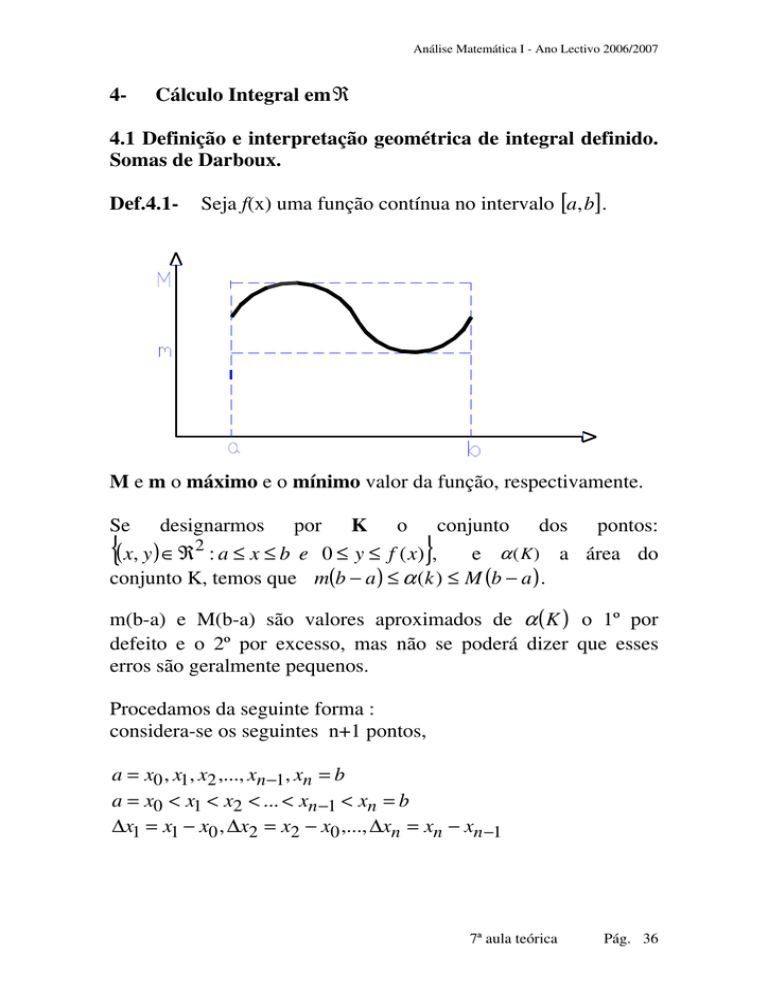
Seja f(x) uma função contínua no intervalo [a, b].
M e m o máximo e o mínimo valor da função, respectivamente.
Se designarmos por K o conjunto dos pontos:
( x, y ) ∈ ℜ2 : a ≤ x ≤ b e 0 ≤ y ≤ f ( x) , e α ( K ) a área do
conjunto K, temos que m(b − a ) ≤ α (k ) ≤ M (b − a ) .
{
}
m(b-a) e M(b-a) são valores aproximados de α (K ) o 1º por
defeito e o 2º por excesso, mas não se poderá dizer que esses
erros são geralmente pequenos.
Procedamos da seguinte forma :
considera-se os seguintes n+1 pontos,
a = x0 , x1, x2 ,..., xn −1, xn = b
a = x0 < x1 < x2 < ... < xn −1 < xn = b
∆x1 = x1 − x0 , ∆x2 = x2 − x0 ,..., ∆xn = xn − xn −1
7ª aula teórica
Pág. 36
Análise Matemática I - Ano Lectivo 2006/2007
Como a função f(x) restringida a cada intervalo
(I=1,…n), é contínua, tem máximo M i e mínimo mi .
[xi −1, xi ]
Designamos por sn = m1∆x1 + m2 ∆x2 + ...mn ∆xn
e sn = M1∆x1 + M 2 ∆x2 +...+ M n ∆xn
sn - designa-se soma inferior e sn soma superior.
Como mi ≤ M i , naturalmente sn ≤ sn
Consideremos xi −1<ξi < xi ,
mi ≤ f (ξi ) ≤ M i
n
mi ∆xi ≤
i =1
ξi é arbitrário
mi ∆xi ≤ f (ξi ) ∆xi ≤ M i ∆xi
n
i =1
f (ξi ) ∆xi
≤
n
i =1
M i ∆xi ⇔ sn ≤ sn ≤ sn
soma integral para a função f(x)
Quando máx. ∆xi → 0 ( n → +∞ ) se as somas integrais tiverem o
mesmo limite I, diz-se que f(x) é integrável no intervalo [a, b] e o
limite I chama-se integral definido da função f(x) no
intervalo [a, b] .
lim
n
b
f(ξi )∆xi = f ( x)dx
max ∆xi → 0 i =1
a
7ª aula teórica
Pág. 37
Análise Matemática I - Ano Lectivo 2006/2007
a - Limite inferior do integral
b - Limite superior do integral
X - variável de integração
Teorema 4.2 Se f(x): [a, b] → ℜ
integrável no intervalo [a, b].
é continua então f(x) é
Teorema4.3 Se f: [a, b] → ℜ é integrável e f(x) ≥ 0, ∀x ∈ [a, b]
então:
b
f ( x )dx ≥ 0
a
4.2 Propriedades do Integral Definido
Teorema 4.4
Seja f: [a , b] → ℜ uma função integrável e K uma
b
b
a
a
constante então: kf ( x )dx = k f ( x )dx
Teorema 4.5
b
Sejam f e g: I → ℜ (I= [a , b] ) integráveis, então:
b
b
a
a
a
Teorema 4.6
Sejam f e g: I → ℜ integráveis, e f(x) ≤ g(x) ∀ x∈I ,
f ( x ) + g ( x )dx = f ( x )dx + g ( x )dx
então:
b
b
f ( x )dx ≤ g ( x )dx
a
a
Prop. 4.7 Seja f: I → ℜ uma função integrável, e m, M o valor
mínimo e o valor máximo da função em I, então:
b
m(b − a ) ≤ f ( x )dx ≤ M (b − a )
a
Teorema 4.8
b
a
c
Seja f: I → ℜ uma função integrável, e c ∈I , então
b
f ( x )dx = f ( x )dx + f ( x )dx
a
c
7ª aula teórica
Pág. 38
Análise Matemática I - Ano Lectivo 2006/2007
Teorema 4.9- Regra de Newton-Leibnitz ou de Barrow
Seja f: [a , b] → ℜ uma função contínua, então:
b
f ( x )dx = F (b) − F (a )
a
onde F(a) e F(b) designam os valores de uma primitiva de f(x),
calculados nos pontos a e b, respectivamente.
b
Notação: f ( x )dx = [ F ( x )]ba = F (b) − F (a )
a
1
Calcule: x 2 + 3 dx
−2
4.3. Métodos de Cálculo
4.3.1. Mudança de variável.
Teorema 4. 10 Seja f: [a , b] → ℜ uma função contínua e x= ϕ (t ), tal
que ϕ (t ) e ϕ ′ (t ) são contínuas no intervalo [α , β ] com ϕ (α ) = a e
ϕ ( β ) = b . Se f [ϕ (t )] está definida e é contínua no intervalo [α , β ]
então:
b
β
f ( x )dx =
α
a
f [ϕ (t )]ϕ ′(t )dt
4.3.2. Integração por partes.
b
b
b
u ′vdx = uv a − uv ′dx
a
a
[ ]
ou
b
b
b
fgdx = Fg a − Fg ′dx
a
a
[ ]
7ª aula teórica
Pág. 39
Análise Matemática I - Ano Lectivo 2006/2007
5.
Alargamento do conceito de integral
5.1. Integrais com limites infinitos
Def. 5.1 Seja uma função contínua definida num intervalo
+∞
[a,+∞[, então:
t →+∞
a
Se o limite
integral
f ( x )dx = lim
t
lim
t →+∞
+∞
t
f ( x )dx
f ( x )dx
a
existe e é finito diz-se que o
a
f ( x )dx existe ou converge.
a
Se o limite não existe ou é infinito diz-se que o integral não existe
ou diverge.
Analogamente:
a
f ( x )dx = lim
t →−∞
−∞
+∞
f ( x )dx =
−∞
Exercício:
c
f ( x )dx +
−∞
+∞
e
+∞
2
0 1+ x
f ( x )dx
t
f ( x )dx = lim
t →−∞
c
1
a
c
s
f ( x )dx + lim
s →+∞
t
f ( x )dx
c
dx
5.2. Integral de uma função descontínua
Seja f(x) uma função definida num intervalo
descontínua em b, então
b
a
f ( x )dx = lim
−
t
t →b a
[a ,b[ e f(x)
f ( x )dx .
O integral diz-se convergente se o limite existir e for finito e
divergente no caso contrário.
7ª aula teórica
Pág. 40
Análise Matemática I - Ano Lectivo 2006/2007
Seja
b
f(x)
uma
c
função
descontinua
b
t
c
t →c− a
f ( x )dx = f ( x )dx + f ( x )dx = lim
a
a
em
f ( x )dx + lim
c ∈ [ a , b] ,
então:
b
t →c+ t
f ( x )dx
Note: os integrais em 5.1 e 5.2 dizem-se integrais impróprios.
Exemplos:
a)
1
0
1
dx
1− x
1
b)
1
2
−1 x
dx
6.1 Conjuntos em ℜ 2
6.1.1 Sistema de coordenadas rectangulares e polares.
Sistema de coordenadas rectangulares
Habitualmente, considera-se duas rectas perpendiculares e a
mesma unidade de comprimento em ambas, para representar o
conjunto ℜ 2 , e três rectas, perpendiculares duas a duas para
representar o conjunto ℜ3 .
ℜ2
Y
P(x,y)
y
x
0
X
ℜ3
Z
z
P(x,y,z)
y
Y
x
X
7ª aula teórica
Pág. 41
Análise Matemática I - Ano Lectivo 2006/2007
Sistema de coordenadas polares
Um sistema utilizado por vezes, para representar o conjunto ℜ 2 ,
é o designado por sistema de coordenadas polares, e consiste em
definir cada ponto P ∈ ℜ 2 por dois valores; ρ distância à origem
e θ o ângulo formado pelas semi-rectas OX, OP.
Assim P fica definido pelo par ( ρ , θ ), em que ρ ≥ o e θ ∈[o,2π [
ℜ2
y
P
ρ
θ
0
x
Existe naturalmente uma correspondência entre os dois sistemas
de coordenadas:
x = ρ cos(θ )
y = ρsen(θ )
ρ = x2 + y2
e
θ = arctg
y
x
7. Aplicações geométricas
7.1
Cálculo de áreas em coordenadas rectangulares
1º caso
Se f(x) ≥ o, ∀x ∈[a , b] e f(x) integrável em [a , b] , então:
coincide
K=
com
a
{(x, y) ∈ℜ :a ≤ x ≤ b ∧ 0 ≤ y ≤ f ( x)}
área
do
b
f ( x ) dx
a
conjunto
2
f(x)
K
a
Exemplo: Calcule a área
b
y = 3x 2 , x = −2 , x = 1 e o eixo OX
7ª aula teórica
Pág. 42
Análise Matemática I - Ano Lectivo 2006/2007
2º caso
Se f(x) muda de sinal um número finito de vezes, a área,
delimitada pelo gráfico de f(x) e pelo eixo OX determina-se
b
por f (x)dx =[ F(x)]ba = F(b) − F(a)
ou,
determinando
as
raízes
a
A= A 0 + A 1 + A 2 +...+ A n + A n + 1
Exemplo: Determine a área delimitada por: y=sen(x), eixo OX ,
x=0 e x=2 π
3º caso
Seja f(x), g(x) definidas em [a , b] e f(x) ≥ g(x), ∀x ∈[a , b] a área
delimitada pelas curvas f(x) e g(x) e pelas rectas x=a e x=b é dada
b
b
b
a
a
a
por: ( f ( x) − g( x))dx = f ( x)dx − g( x)dx
f(x)
A
g(x)
Exemplo: Determine a área limitada por:
y = x2 e y = x
7.2
A=
Cálculo de áreas em coordenadas polares
θ2
1
ρ 2 dθ
2θ
1
Exercício: calcule a área de uma circunferência de raio r.
7ª aula teórica
Pág. 43
Análise Matemática I - Ano Lectivo 2006/2007
7.3 Cálculo do comprimento de um arco em coordenadas
rectangulares.
Seja f(x) uma função definida em [a , b] , o comprimento do arco
f(a), f(b) sobre o gráfico de f(x) é dado por: S =
b
1 + ( f ′( x)) dx
2
a
f(x)
a
7.4
b
Cálculo do Volume de um sólido de revolução
Seja f(x) definida no intervalo [a , b] , o volume gerado pela
rotação da área limitada pela curva y=f(x) em torno do eixo OX é
dado por:
b
2
b
V = πf ( x)dx = π f 2 ( x)dx
a
a
Exemplo: Determine o volume de revolução gerado pela rotação
de 2 π da região A= ( x, y) ∈ℜ 2 :0 ≤ y ≤ e x − 1 ∧ 0 ≤ x ≤ 1 , em torno do
{
}
eixo do X.
7ª aula teórica
Pág. 44