Questão 1 (triret70

Razões Trigonométricas
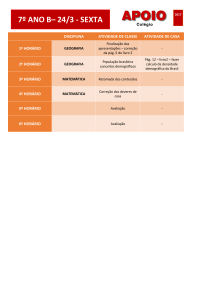
Questão 1 (triret70.rtf)
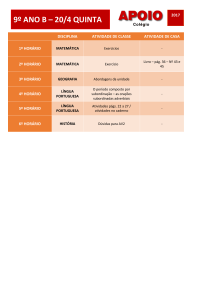
Questão 2 (clairault01.rtf)
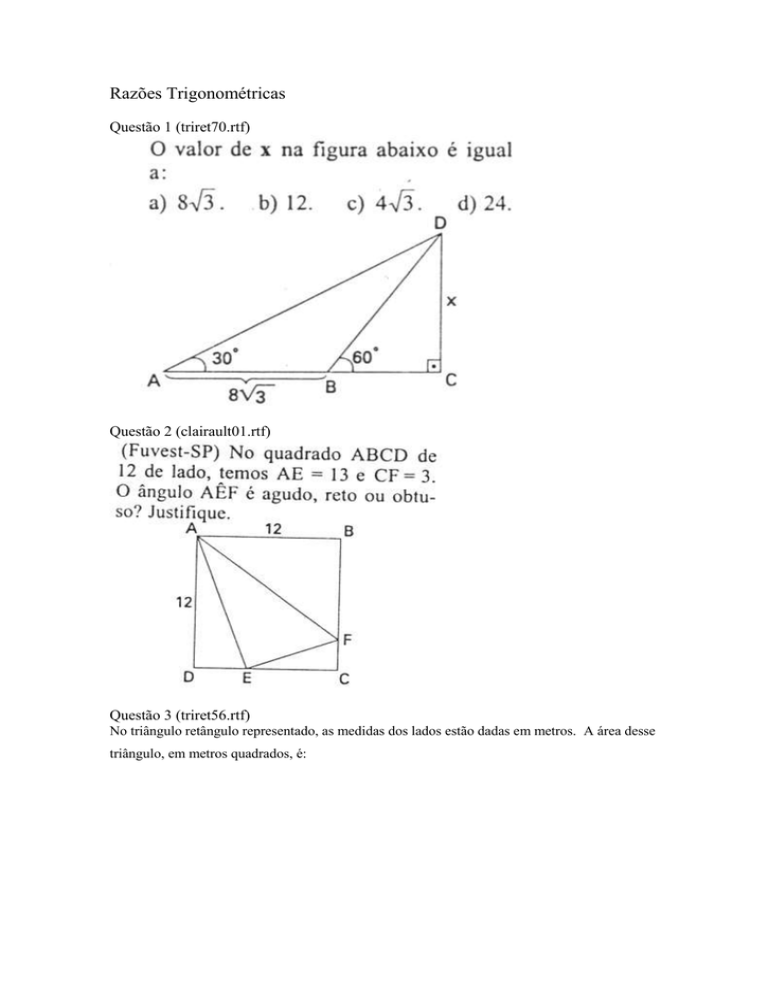
Questão 3 (triret56.rtf)
No triângulo retângulo representado, as medidas dos lados estão dadas em metros. A área desse
triângulo, em metros quadrados, é:
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
2/21
a) 30
b) 27
c) 24
d) 20
x
x-1
e) 18
x-8
Questão 4 (triret77.rtf)(ESPM_nov_2004, cod_e)
A figura abaixo representa uma praça de forma triangular, sendo que o ângulo  é reto. Duas pessoas
percorrem o contorno da praça a partir do ponto A, mas em sentidos contrários, até se encontrarem num
ponto P do lado BC. Sabendo-se que elas percorreram distâncias iguais, podemos concluir que a distância
do ponto P ao ponto A, em linha reta é de, aproximadamente: (adote
a) 22m;
b) 25m;
c) 27m;
d) 30m;
e) 32m.
Questão 5 (r_trigo_ufba23.rtf)
(Ufba_2003_2f, q cod_)
2  2, 25 )
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
Questão 6 (raz_trigouem55.rtf)(Uem_2004, cód_t0)
Para obter a altura CD de uma torre, um
matemático, utilizando um aparelho,
estabeleceu a horizontal AB e determinou as
medidas dos ângulos = 30° e = 60° e a
medida do segmento BC = 5m, conforme
especificado na figura. Nessas condições, a
altura da torre, em metros, é...
Questão 7 (razaotrigo11.rtf)
Questão 9 (razatrigo11.doc)(UNEB, cód_L)
Seja o ponto M, no interior do quadrado ABCD, conforme a figura abaixo.
Se MH = 4
cm, o perímetro do quadrado, em centímetros, :
3/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
a)
64
b)
64
c)
128
d)
128
e)
256
Questão 10 (razatrigo13.doc)Fat_2004
Na circunferência trigonométrica abaixo, considere o

arco AM , de medida
radianos.
3
Então,
a) AP  1
b) MN 
3
c) ON 
2
1
3
e) OP  2
d) AN 
Questão 11 (razatrigo68.rtf)(Fuvestá-SP)
Calcule a medida x indicada na figura abaixo.
4/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
5/21
Resp. 50
Questão 12 (raztrigo14.rtf)(Santa Casa-SP)
Na figura, o perímetro do triângulo ACD, :
a)
1,5
b)
c)
3
d)
3+
e)
3+
Questão 13 (raztrigo15.rtf)(cod_ L)
Sabendo que AC é o diâmetro de uma circunferência de raio igual a 10cm e centro O.
A medida da corda AB , em cm:
a)10
b)20
c)30
d)40
e)50
Questão 14 (raztrigo16.rtf)
(UF-Viosa)
a)
O cosseno do ângulo
, assinalado na figura, :
0,5
b)
c)
d)
.
e)
Questão 15 (raztrigo18.rtf)
(PUC-SP-81) Qual o valor de x na figura ao lado ?
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
6/21
a)
b)
c)
d)
e)
Questão 16 (raztrigo21.rtf)
Na figura abaixo, h =
,
= 300 e
= 600. Calcule a medida x + y.
Resp.
Questão 17 (raztrigo22.rtf)
Na figura AB um arco de uma circunferência de raio 1. A area do trapézio retângulo BCDE :
Questão 18 (raztrigo23.rtf)
Para determinar a altura de uma torre, um topógrafo coloca o teodolito a 100 m da
base e obtém um ângulo de 300, conforme mostra a figura. Sabendo que a luneta do
teodolito está a 1,70 do solo, qual aproximadamente a altura da torre? (Dados: sen300
= 0,5; cos300 = 0,87 e tg300 = 0,58).
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
7/21
Questão 19 (raztrigo24.rtf)
Em um exercício de tiro, o alvo se encontra numa parede e sua base está situada a 20
m do atirador. Sabendo que o atirador v o alvo sob um ângulo de 100 em relação
horizontal, calcule a que distância a mosca do alvo se encontra do cho. (Dados: sen100
= 0,17; cos100 = 0,98 e tg100 = 0,18).
Questão 20 (raztrigo26.rtf)
(Mack-SP)
a)
b)
c)
Na figura, o valor de senx
0,5
1/3
1/6
d)
e)
Questão 21 (raztrigo27.rtf)
(Mack-SP)
Sendo O o centro da circunferência de raio unitário, então x=BC vale:
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
a)
1
b)
0,8
c)
0,6
d)
0,5
e)
0,4
8/21
Questão 22 (raztrigo38.rtf)
Ufabc_2006.2, q44_cod_V
Lua entrará na fase quarto minguante
às 16:13 de amanhã
Quando a Lua está no quarto minguante, ocasião na qual, vista da Terra, exatamente metade
dela aparece iluminada pelo Sol, o triângulo TLS, indicado na figura, é retângulo em L.
Sabendo-se que, na situação descrita, a medida do ângulo LSˆT é 0,15°, e adotando sen 0,15°
= 0,0025, é correto dizer que a distância Terra-Sol é igual à distância Terra-Lua multiplicada
por
a) 200.
b) 250.
c) 300.
d) 350.
e) 400.
Questão 23 (raztrigo41.rtf)(UPF_RS_2005, q29)
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
9/21
Questão 24 (raztrigo42.rtf)
( EPCAR_AGO/2005, cód_L )
Um piloto de avião, a uma altura de 3100 m em relação ao solo, avista o ponto
mais alto de um edifício de 100 m de altura nos instantes T1 e T2, sob os ângulos
de 45° e 30°, respectivamente, conforme a figura seguinte:
A distância percorrida pelo avião entre T1 e T2, é, em m,
igual a
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
10/21
Questão 25 (raztrigo44.rtf)( EPCAR_AGO/2002, cód_E)
Um avião está voando em reta horizontal à altura 1 em relação
a um observador O, situado na projeção horizontal da trajetória.
No instante to, é visto sob ângulo alfa de 30° e, no instante t1, sob
ângulo beta de 60°.
Questão 26 (raztrigo60.rtf)
(Santa Casa-SP)
a)
Na figura, o perímetro do triângulo ACD, :
1,5
b)
c)
3
d)
3+
e)
3+
Questão 27 (raztrigo78.rtf)
Espm_2005, q39
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
11/21
Questão 28 (raztrigo83.rtf)
Considere o trapézio retângulo representado na figura abaixo,
cujas medidas dos lados são dadas em centímetros.
(Ucsal, 2001.1, cod_L)
A área desse trapézio, em centímetros quadrados, é
a) 48 3
b) 45 3
c) 42 3
d) 36 3
e) 30 3
Questão 29 (raztrigo84.rtf)
Suponha que nos pontos A e B da figura abaixo localizam-se
dois observatórios num mesmo plano e que, num dado momento, um balão é visto
pelos dois sob ângulos de 40º e 70º.
(Bahiana, 2001_cod_f)
Dados:
tg 40º = 0,84
tg 70º = 2,73
Se a distância entre os dois observatórios é de 27 km, a que altura o balão está do
solo?
a) 36,48 km
e) 30,28
b) 35,24 km
c) 34,72 km
d) 32,76 km
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
Resoluçao da questão 1 (triret70_res.rtf)
Resoluçao da questão 2 (clairault01_res.rtf)
Resolução
Teorema de Clairault
EF 2  32  7 2  58  EF  58
AF 2  12 2  9 2  225  AF  15
15 2  58  132  225  58  169  agudo
Resoluçao da questão 3 (triret56_res.rtf)
Não disponivel
Resoluçao da questão 4 (triret77_res.rtf)
Resolução c)
Resoluçao da questão 5 (r_trigo_ufba23_res.rtf)
Não disponivel
Resoluçao da questão 6 (raz_trigouem55_res.rtf)
Resolução ® 20
12/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
Resoluçao da questão 7 (razaotrigo11_res.rtf)
Resolução


6 3
 3  y  30 0  60 0  y  30 0
6
BC
6 3
tg 30 0 
 BC 
2 3
6
3
x 6 32 3  4 3
tg y  30 0 
Resoluçao da questão 9 (razatrigo11_res.doc)
Resolução: 64
Seja o ponto M, no interior do quadrado ABCD, conforme a figura abaixo.
Se MH = 4
cm, o perímetro do quadrado, em centímetros, :
13/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
3 4 3

 BH  12
3
BH
4 3
tg 60 0  3 
 HC  4
HC
tg30 0 
O perímetro do quadrado 2p=4x4=16 cm
Resoluçao da questão 10 (razatrigo13_res.doc)
Resolução
Na circunferência trigonométrica abaixo, considere o
arco AM , de medida

radianos.
3
3
1/ 2
1
Os triângulos OMN e OAP são semelhantes:
 2 
 OP  2 .
1
AP OP
Resoluçao da questão 11 (razatrigo68_res.rtf)
Resolução x=50
Resp. 50
O triângulo que tem um ângulo de 300 é isósceles, com dois lados medindo 100 u.c.
0
A medida de x é: sen30 
x
1
x
 
 x
100
2 100
Resoluçao da questão 12 (raztrigo14_res.rtf)
Resolução:
Na figura, o perímetro do triângulo ACD, :
14/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
15/21
3 AD

 AD  3
; o perimetro do triângulo isósceles ADC: 2 p  1  1  2
2
2
DC  1  3  3  1
sen60 0 
Resoluçao da questão 13 (raztrigo15_res.rtf)
Resolução: a)
Sabendo que AC é o diâmetro de uma circunferência de raio igual a 10cm e centro O. A medida da corda AB , em
cm:
cos 30 0 
AB
3

 AB  10 3
20
2
Resoluçao da questão 14 (raztrigo16_res.rtf)
Resolução: d)
O cosseno do ângulo , assinalado na figura, :
2
1
1
sen      cos 2   1  c
2
2
Resoluçao da questão 15
Resolução:
Qual o valor de x na figura ao
y  x  ? e h  altura
(raztrigo18_res.rtf)
lado ?
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
16/21
y
3

 y  20 3
40
2
h
h
3
tg 30 0  

 h  20
y
3
20 3
cos 30 0 
tg 60 0 
h
20
3
20 3


x
x
x
1
3
Resoluçao da questão 16 (raztrigo21_res.rtf)
Resolução
Resp.
x
3
6
 x
. 2
h
2
2 , a soma x+y= 6  6  3 6
Cálculo de x e de y:
2
2
y
tg   y  3. 2  6
h
tg 
Resoluçao da questão 17 (raztrigo22_res.rtf)
Resolução
Na figura AB um arco de uma circunferência de raio 1. A area do trapézio retângulo BCDE é:
0
Cálculo de DE: sen30 
DE
1
OE
3
 DE  ; cálculo de OE: cos 30 0 
; cálculo de BC:
 OE 
1
2
1
2
1
DC
3
tg 30  2 
 DC 
1
3
3
2
0
Cálculo da área do trapézio BCDE: Atrap
1


  3 .1  3 
 2 3 
2 
b  B .h  


2
2
Resoluçao da questão 18 (raztrigo23_res.rtf)
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
17/21
Não disponivel
Resoluçao da questão 19 (raztrigo24_res.rtf)
Não disponivel
Resoluçao da questão 20 (raztrigo26_res.rtf)
Resolução:
O ângulo BOC mede 300, o lado BO=raio=1:
sen30 0 
x
x 1
1
  x
1
1 2
2
Resolução:
O segmento OP é raio da circunferência e OC é a hipotenusa do triângulo retângulo POC, pelo teorema de Pitágoras:
senx 
2 1

6 3
Resoluçao da questão 21 (raztrigo27_res.rtf)
Não disponivel
Resoluçao da questão 22 (raztrigo38_res.rtf)
Resolução: e)
Quando a Lua está no quarto minguante, ocasião na
qual, vista da Terra, exatamente metade dela aparece
iluminada pelo Sol, o triângulo TLS, indicado na figura,
é retângulo em L.
Representando por s a distância da Terra ao Sol e por l (ele) a distância da Terra à Lua, temos:
l
l
l
l
senLST    sen 0,150   0,0025   s 
 s  400.l
s
s
s
0,0025


Resoluçao da questão 23 (raztrigo41_res.rtf)
Resolução:
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
18/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
Resoluçao da questão 24 (raztrigo42_res.rtf)
Resolucao a)
A distância percorrida pelo avião entre T1 e T2, é, em m,
igual a
Resoluçao da questão 25 (raztrigo44_res.rtf)
Resolução c)
19/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
?=x
3
1

3
ax
3 1
1
tg 60 0 
 a 
1
a
3
tg 30 0 
Resoluçao da questão 26 (raztrigo60_res.rtf)
Não disponivel
Resoluçao da questão 27 (raztrigo78_res.rtf)
Resoluçao da questão 28 (raztrigo83_res.rtf)
RESOLUÇÃO
Resp: A
h
h
3
 sen60º 

8
8
2
hh
h= 4 3
m
m
1
 cos60º 

 m 4
8
8
2
Base maior: 10 + m = 14
m
20/21
Arquivo: raztrigo2008.dcs,28/5/2017,17:37:51, Pág
Área =
 
Bb
14  10
h
4 3  48 3
2
2
Resoluçao da questão 29 (raztrigo84_res.rtf)
RESOLUÇÃO
Resp: D
Sejam C o pé da perpendicular ao plano passando pelo balão e h sua altura.
Então.
h
h

 2,73  h  2,73x
BC
x
h
h
tg40 0 

 0,84  h  22,68  0,84x
27  x
27  x
tg70 0 
2,73 x = 22,68 + 0,84 x
1,89 x = 22,68  x = 12
Portanto, h = (2,73) (12) = 32,76 km
. Então
21/21