IGL - UERJ - lista 1

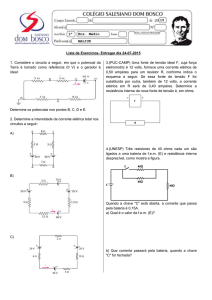
1. (Uerj 2011) No circuito abaixo, o voltímetro V e o amperímetro A indicam, respectivamente,
18 V e 4,5 A.
Considerando como ideais os elementos do circuito, determine a força eletromotriz E da
bateria.
2. (Uerj 2010) O circuito elétrico de refrigeração de um carro é alimentado por uma bateria
ideal cuja força eletromotriz é igual a 12 volts.
Admita que, pela seção reta de um condutor diretamente conectado a essa bateria, passam no
mesmo sentido, durante 2 segundos, 1,0 × 1019 elétrons.
Determine, em watts, a potência elétrica consumida pelo circuito durante esse tempo.
Considere o módulo da carga do elétron igual 1,6  10–19 C.
TEXTO PARA A PRÓXIMA QUESTÃO:
A tabela abaixo mostra a quantidade de alguns dispositivos elétricos de uma casa, a potência
consumida por cada um deles e o tempo efetivo de uso diário no verão.
Dispositivo
Quantidade
Potência (kW)
Tempo efetivo de uso diário (h)
ar-condicionado
2
1,5
8
geladeira
1
0,35
12
lâmpada
10
0,10
6
Considere os seguintes valores:
• densidade absoluta da água: 1,0 g/cm 3
• calor específico da água: 1,0 cal.g-1 0C-1
• 1 cal = 4,2 J
• custo de 1 kWh = R$ 0,50
3. (Uerj 2010) Durante 30 dias do verão, o gasto total com esses dispositivos, em reais, é
cerca de:
a) 234
b) 513
c) 666
d) 1026
4. (Uerj 2009) Na tabela abaixo, são apresentadas as resistências e as d.d.p. relativas a dois
resistores, quando conectados, separadamente, a uma dada bateria.
Considerando que os terminais da bateria estejam conectados a um resistor de resistência
igual a 11,8 Ω , calcule a energia elétrica dissipada em 10 segundos por esse resistor.
5. (Uerj 2008) O circuito a seguir é utilizado para derreter 200 g de gelo contido em um
recipiente e obter água aquecida.
E: força eletromotriz do gerador
r: resistência interna do gerador
R1, R2 e R3: resistências
C: chave de acionamento
A: recipiente adiabático
No momento em que a chave C é ligada, a temperatura do gelo é igual a 0°C.
Estime o tempo mínimo necessário para que a água no recipiente A atinja a temperatura de
20°C.
Dados:
Calor específico da água 1 cal/g °C
Calor latente de fusão do gelo 80 cal/g
1 cal 4,2 J
6. (Uerj 2015) Partículas de carga elétrica q e massa m penetram no plano horizontal de uma
região do espaço na qual existe um campo magnético de intensidade B, normal a esse plano.
Ao entrar na região, as partículas são submetidas a um selecionador de velocidades que deixa
passar apenas aquelas com velocidade v 0 .
Admita que, na região do campo magnético, a trajetória descrita por uma das partículas
selecionadas seja circular.
Escreva a expressão matemática para o raio dessa trajetória em função de:
- massa, carga e velocidade da partícula;
- intensidade do campo magnético.
7. (Uerj 2010) As superfícies refletoras de dois espelhos planos, E1 e E2, formam um ângulo á.
O valor numérico deste ângulo corresponde a quatro vezes o número de imagens formadas.
Determine á.
8. (Uerj 2011) Um raio de luz vindo do ar, denominado meio A, incide no ponto O da superfície
de separação entre esse meio e o meio B, com um ângulo de incidência igual a 7º.
No interior do meio B, o raio incide em um espelho côncavo E, passando pelo foco principal F.
O centro de curvatura C do espelho, cuja distância focal é igual a 1,0 m, encontra-se a 1,0 m
da superfície de separação dos meios A e B.
Observe o esquema:
Considere os seguintes índices de refração:
- nA = 1,0 (meio A)
- nB = 1,2 (meio B)
Determine a que distância do ponto O o raio emerge, após a reflexão no espelho.
Gabarito:
Resposta da questão 1:
Dados: UCD = UBE = 18 V; i2 = 4,5 A.
1ª Solução:
No resistor R3:
UCD = R3 i3  18 = 12 i3  i3 = 1,5 A.
A corrente total é:
i = i2 + i3 = 4,5 + 1,5  i = 6 A.
Aplicando a Lei de Kirchoff na malha ABCDEFA:
E – R1 i – UCD – R4 i = 0  E = 3 (6) + 18 + 4 (6)  E = 60 V.
2ª Solução:
No resistor R3:
UCD = R3 i3  18 = 12 i3  i3 = 1,5 A.
No resistor R2:
UBE = R2 i2  18 = R2 (4,5)  R2 = 4 Ω .
A corrente total é:
i = i2 + i3 = 4,5 + 1,5  i = 6 A.
Calculando a resistência equivalente do circuito:
R  R3
12  4
 R4  Req  3 
 4  Req = 10 .
Req = R1  2
R 2  R3
12  4
Aplicando a Lei de Ohm-Pouillet:
E = Req i  E = 10 (6)  E = 60 V.
Resposta da questão 2:
Dados: t = 2 s; n = 1,0  1019; E = 12 V; e = 1,6  10–19 C.
A carga (Q) que passa pela secção reta do condutor nesse intervalo de tempo é:
Q = n e, sendo e a carga elementar: Assim:
Q = 1019 (1,6  10–19)  Q = 1,6 C.
A corrente elétrica é a razão entre a carga que passa e o tempo de passagem:
I=
Q 1,6
 i = 0,8 A.

t
2
A potência consumida pelo circuito é igual a potência gerada pela bateria.
Pcons = Pgerada = E i = 12 (0,8) 
Pcons = 9,6 W.
Resposta da questão 3:
[B]
Sendo N a quantidade de dispositivos, P a potência elétrica e t, o tempo efetivo de uso diário,
e C (R$ 0,50) o custo do kWh, o gasto diário dos dispositivos é:
G = N  P  t  C.
Através desse calculo, completemos a tabela abaixo.
Dispositivo
N
P (kW)
t(h)
Gasto diário (R$)
ar-condicionado
2
1,5
8
2  1,5  8  0,50 = 12,00
geladeira
1
0,35
12
1  0,35  12  0,50 = 2,10
lâmpada
10
0,10
6
10  0,1  6  0,50 = 3,00
O gasto mensal (30 dias) é:
GMensal = 30 ( 12,00 + 2,10 + 3,00) = 30 (17,10)  GMensal = R$ 513,00.
Resposta da questão 4:
Para o primeiro resistor  U = r.i  11,6 = 5,8.i  i = 2 A
Para o segundo resistor  U = r.i  11,4 = 3,8.i  i = 3 A
Estas são as correntes que a bateria forneceu para cada resistor na sua vez.
Isto significa pela lei de Pouillet
E
r  R 
E
2
r  5,8
E
3
r  3,8 
i 
Onde E e r são os parâmetros da bateria, ou seja, força eletromotriz e resistência interna.
2/3 = (r + 3,8)/(r + 5,8)
3(r + 3,8) = 2(r + 5,8)
3r + 11,4 = 2r + 11,6
r = 11,6 – 11,4 = 0,2 Ω
E = 2.(r + 5,8) = 2.6 = 12 V
Considerando agora o novo resistor de 11,8 Ω
i
E
12
12


 1A
r  R 0,2  11,8  12
A energia dissipada é Energia = P. Δ t = R.i2.  t = 11,8.12.10 = 118 J
Resposta da questão 5:
Aplicando a Lei de Ohm-Pouillet ao circuito dado, calculamos a corrente elétrica.
E
100
i

 i  5 A.
Req
20
A potência dissipada em R3 é:
P  R3 i 2  8  52  P  200 W.
Quantidade de calor envolvida no processo:
Q  Qgelo  Qágua  m Lg  m ca Δθ  200  80  200  1  20  0   20.000 cal 
Q  20.000  4,2  84.000 J.
Admitindo que toda a potência liberada no resistor R3 seja absorvida pelo gelo e pela água:
Q
Q 84.000
420
P
 Δt  
 420 s 
min 
Δt
P
200
60
Δt  7 min.
Resposta da questão 6:
Se o movimento é circular uniforme, a força magnética atua como resultante centrípeta.
Fmag  Rcent  q v B 
m v2
R

R
mv
.
qB
Resposta da questão 7:
Dado:  = 4 n.
O número de imagens (n) obtidas pela associação de dois espelhos planos que formam entre
si um ângulo  (em graus) é dado pela expressão:
n=
360
 1 . Assim:

n
360
 1 (M.M.C. = 4 n) 
4n
4 n2 = 360 – 4 n  n2 + n – 90 = 0. Aplicando a fórmula de Baskara:
n=
1  12  360 1  19

. Ignorando a resposta negativa, temos:
2
2
18
 n  9.
2
Como:  = 4 n 
= 36°
n
Resposta da questão 8:
Dados: nA = 1,0; nB = 1,2; sen 7° = 0,12.
A figura a seguir ilustra a situação. Como o raio refratado incide no espelho passando pelo
foco, ele reflete paralelo ao eixo principal.
Sabemos que quando um ângulo é pequeno ( < 10°), podemos fazer a aproximação:
sen  = tg  = (radiano).
Como nesse caso i = 7° e r < i (ângulos pequenos), podemos então trocar o seno pela
tangente na lei de Snel. Assim:
0,12
nA tg i = nB tg r  1 (0,12) = 1,2 tg r  tg r =
 tg r = 0,1.
1,2
Mas no triângulo OPB destacado na figura:
d
d
tg r =
 0,1 =  d = 0,3 m = 30 cm.
3
3