7,0 − = BB VV Mas, Portanto 1-1 Portanto, CI , praticamente

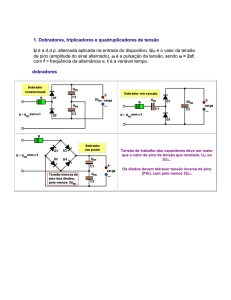
ESTABILIZAÇÃO DA CORRENTE DE COLETOR DO TRANSISTOR
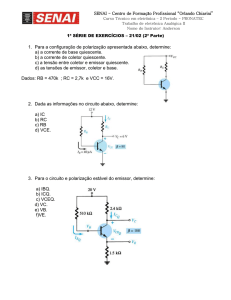
Estabilização ideal
RC
VCC
IE
VBB
RE
VE
V BB = 0,7 + VE
V E = VBB − 0,7
IE =
VE V BB − 0,7
=
RE
RE
Mas, I C ≈ I E
Portanto
IC ≈
V BB − 0,7
RE
1-1
Portanto, I C , praticamente, não depende do valor de β
Exemplo de dimensionamento da polarização do transistor.
Seja
VCC = 12 v ,
VCE = 5 v ,
VE =
V E = I E RE ≈ I C RE
RE ≈
VE
0,6
=
= 200 Ω
I C 3 × 10 −3
− 12 + I C RC + VCE + VE = 0
Ou
− 12 + I C RC + 5 + 0,6 = 0
1
12
v = 0,6 v ,
20
I C = 3 mA
Portanto:
RC =
12 − 5 − 0,6
6,4
=
= 2,13 kΩ
IC
3 × 10 −3
V BB = 0,7 + V E = 0,7 + 0,6 = 1,3 v
Circuito final
2,13 kΩ
12 v
5 v
3 mA
1,3 v
200 Ω
0,6 v
Excitação de sinal alternado
2,13 kΩ
12 v
eS
1,3 v
200 Ω
Entretanto, normalmente a tensão de excitação é aterrada.
Método 1: uso de transformador:
2,13 kΩ
12 v
eS
1,3 v
200 Ω
2
Método 2: Resistor em série com a tensão de alimentação V BB
C
IB
RB
eS
VBB
IE
RE
O capacitor C é curto circuito para AC e circuito aberto para DC
Cálculo da polarização:
− VBB + I B R B + 0,7 + I E RE = 0
Mas, I E ≈ I C = β I B
Portanto
− VBB + I B RB + 0,7 + βI B R E = 0
ou I B =
V BB − 0,7
RB + βR E
Mas I C = βI B
Portanto
IC =
β (V BB − 0,7 )
RB + βRE
Note que I C depende do valor de β .
Entretanto, se escolhermos RB , de tal modo que
R B << βR E
V BB − 0,7
1-2
RE
Vemos, que neste caso, o efeito do valor de β se torna desprezível.. Nota-se que a
equação 1-2 é aproximadamente igual a equação 1-1.
Então,
IC ≈
Exemplo: Seja β = 300 e RE = 200 Ω
3
Neste caso,
βRE = 60 kΩ
Poderemos adotar RB = 0,1βR E = 6 kΩ
Método 3 – Alimentação de base proveniente de VCC por meio de uma divisão de tensão
Abaixo temos o divisor de tensão e seu equivalente Thevenin-Norton
RB =
R1
VCC
VBB =
R2
VCC R2
R1 + R2
Têm-se duas equações:
VCC R2
= V BB
R1 + R2
R1 R2
= RB
R1 + R2
Resolvendo este sistema resulta:
R1 =
R BVCC
V BB
R2 =
VBB R1
VCC − VBB
Exemplo
Seja a produção de V BB = 1,3 v a partir de VCC = 12 v
Vamos adotar RB = 6 kΩ
Neste caso:
R1 =
6 × 12
= 55,4 kΩ
1,3
R2 =
1,3 × 55,4
= 6,7 kΩ
12 − 1,3
4
R1R2
R1 + R2
Circuito completo:
55,4 kΩ
2,13 kΩ
C
eS
12 v
6,7 kΩ
200 Ω
Circuito equivalente para sinal alternado
Neste caso o capacitor é um curto circuito, assim como todas as tensões DC.
iC
eS
R2
R1
iC ≈ i E =
RC
iE
v0
vE ≈ eS
RE
e
vE
≈ S
RE RE
v0 = −iC RC ≈ −
e S RC
RE
v 0 RC
≈
eS R E
Em nosso exemplo:
v 0 2,13 kΩ
≈
≈ 10,6
eS
0,2 kΩ
Com capacitor de emissor
Supondo curto circuito, do emissor para a terra, em AC, teremos a formula aproximada
para o ganho de tensão:
v0
q
≈
I C RC ≈ 36 I C RC
eS KT
v0
Em nosso exemplo fica:
≈ 36 × 3 × 10 −3 × 2,13 × 10 3 Ω ≈ 230
eS
5