Leis_Kirchhoff_Mar_2012

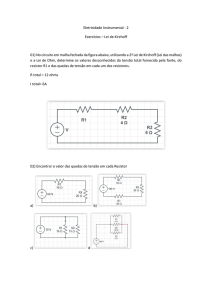
Capítulo 7
Leis de Kirchhoff
LEI DE KIRCHHOFF PARA A TENSÃO (LKT)
A lei de Kirchhoffpara a tensão, ou lei das malhas, afirma que a tensão aplicada a um circuito fechado é igual à
soma das quedas de tensão nesse circuito. Este fundamento foi usado no estudo de circuitos série e foi expresso
da seguinte forma:
Tensão aplicada = soma das quedas de tensão
(7-1)
onde ~A é a tensão aplicada e V~, 112 e 113 são as quedas de tensão.
Uma outra forma de se enunciar a LKT é: a soma algébrica das elevações, ou aumentos, com as quedas de ten
são deve ser iguala zero. Uma fonte de tensão ou fem é considerada como uma elevação de tensão; uma tensão em
um resistor consiste numa queda de tensão. Para ~cilitar a denominação, normalmente se usa índices alfabéticos
para indicar as fontes de tensão e índices numéricos para indicar as quedas de tensão. Esta forma da lei pode ser
escrita transpondo os termos da direita da Equação (7-1) para o lado esquerdo:.
Tensão aplicada — soma das quedas de tensão = O
Substituindo por letras:
Vs—Vi—Vz—V30
ou
Introduzindo um símbolo novo,!, a letra grega maiúscula sigma, temos
(7-2)
na qual LV, a sorna algébrica de todas as tensões ao longo de qualquer circuito fechado, é igual a zero. L significa
“somatório de”.
Atribuímos um sinal positivo (+) para uma elevação de tensão e um sinal negativo (—) para urna queda de tensão na fórmula EV= O (Figura 7-1). Ao percorrer as quedas de tensão ao longo de um circuito, comece no terminal
negativo da fonte de tensão, O percurso do terminal negativo até o terminal positivo, passando pela fonte de tensão
corresponde a uma elevação de tensão. Continuamos a percorrer o circuito do terminal positivo passando por todos
os resistores e voltamos ao terminei negativo da fonte, Na Figura 7-1. se começarmos pelo ponto a, o terminal nega
tivo da bateria, e se percorrermos o circuito no sentido abcda, atravessaremos V~ do — para 0+, assim V~ = +100V.
-
CAPÍTULO 7• LEIS DE KIRc1~n1orF
b~
c
~
E 1’
V2=30V
‘2~
V3=20V
a
123
a
‘2
—
~‘t
—
1’~
1’3
—
100-50—30—20
100—100
=0
=
a
d
Figura 7-1 Ilustração da fórmula XV = 0.
Se partirmos do ponto b e percorreremos o circuito no sentido oposto badcb, atravessaremos V4 do + pano assina
= —100V. A queda de tensão através de qualquer resistência será negativa (—) se a percorreremos no sentido do t
parao-.Assim,naFigura7-l, sepercorre mosocircuitonosentjdoabcd,j, V~=-5OV, V2—30Ve1Ç~=-2OV.A
queda de tensão será positiva (+) se atravessarmos a resistência do sentido do — para o+. Portanto, ao percorreremos
o circuito no sentido abcda, teremos
—,
Lv = o
VÀ
—
Vi
½—
100—50—30 —20
=
O
=
O
0=0
Exemplo 7.1 Determine o sentido da tensão ao longo do circuito abcda (Figura 7-2) e em seguida escreva as expressões
para as tensões ao longo do circuito.
Adote o sentido da corrente conforme indicado na figura. Marque as polaridades + e — de cada resistor.
é urna fonte de tensão
(+).
(É uma elevação de tensão no sentido adotado pan a comute.)
(É uma diminuição no sentido adotado para a corrente.)
(É uma diminuição no sentido adotado.)
(É urna diminuição de tensão no sentido adotado para a corrente.)
(É uma diminuição no sentido adotado.)
duma queda de tensão (—).
V2 duma queda de tensão (—).
6 urna fonte de tensão (—).
1/3 é uma queda de tensão (—).
~1
+VA — i’1 — 1/2 — 1/3
ti,
=
i’3•
=
—
o
=
b
3V
a
VI
6V
VA=ISVS
VI
7
-1-
a
Figura
d
7-2
Ilustração da lei de Kirchhoff
para tensão com
duas fontes.
o
1’3n2V
P7gum 7-3 Determinação de uma fonte de tensão.
124
ELEWIcIDADE BÁSICA
Agrupando os aumentes e as quedas de tensão:
—
(111 + V2 + 1’3 + VB)
Observe que as quedas de tendo incluem urna fonte dc tendo, V,. Normalmente. urna fonte seria positiva. Neste caso,
a polaridade da fonte age contra o sentido siotado para a corrente. Porisato, o seu efeito é o de reduzir a tensão
Exemplo 7.2 Determine a teu sKo V~ (Figura 7-3).
O sentido do fluxo da conente está indicando através da seta. Marquespolaridade das quedas de tensão nos resistores.
Percorra o circuito no sentido do fluxo da cotxeiae partindo do ponto a. Esatva a equaç~o da tensão ao longo dc circuito.
(7-2)
EV=O
Utilize as regras do + e — para os aumentos e quedas de ttns~o respeclivamente.
—
V1
—
—
1’3
=
O
Obtenha o valor de VB.
VB=VA—V1—V2-- V3=15—3—6—2=4V
Resp.
Como se obteve um valor positivo de V~, o sentido adotado para a corr~te ~ de fato o sentido da corrente.
LEI DE KIRCHHOFF PARA A CORRENTE (LKC)
A lei de kirchhoffpara a corrente, ou lei dos nós, afirms que a sorna das correntes que en#um numa junção é igual
a soma das correntes que saem da junção. Suponha que tenhamos seis correntes saindo e entrando numa junção
comum ou ponto, por exemplo, o ponto P (Fipira 7-4). Este ponto comum é também chamado dc nó.
13
Ponto cctnufl3, junção ou ii6
Figura 7-4 As correntes em
Soma de todas as correntes que enitam
um ponto comum.
soma de todas as correntes qcie saem
Substitufdo por letras:
fl + I~3 + 14 + ‘6
12 + 15
se consideramos as contntes que entram numa jun9âo como positivas (÷) e as que saem da mesma junç~o como
negaüvas (—), entilo esta lei afirma tamb4m que a soma algébrica de todas as conentes que se encontram num jun
ção comum é zero. Utilizando o símbolo de somatório, E. temos;
EI
=
O
(7-3)
CAPITULO 7
•
LEIS DE KIRCI*IOFF
125
onde El, a soma algébrica de todas as correntes num ponto comum, ó zero.
1j
—
12 + 13 + 14—13 + 16
=
O
Se transpusermos os termos negativos para o lado direito do sinal de igual, teremos a mesma forma da equação
original.
Exemplo 7.3 Escreva a equaç~o para a corrente 1~, na parte (a) e na parte (b) da Figura 7-5.
la—?.
w.
P
4—.
(a)
{b)
Figura 7-5 Ilustração da ei de Kirchhoff para corrente (LXC).
A soma algébrica de todas as correntes em um nó é zero. As correntes que entram são -1-; as correntes que saem são
—
(a) +11—12—13=0
11I2+ly
Resp.
(1’) +lj—F2—13—14=0
u1l2+13+14
Resp.
Exemplo 7.4 Calcule as correntes desconhecidas na parte a e na parte b da Figura 7-6.
j,
e-
—,
=
2À_,____?S_~
4A
-‘2
7A
(a)
(1’)
Figura 7-6 Determinação da corrente.
A soma algébrica de todas as correntes em um nó é zero. As correntes que en~am são i-; as correntes que saem são—.
(°) —11-1-12—13=0.
li=ka13734A
Resp.
(b) +11+12—13+14=0
t4~I~jI2+l32t3*4lA
Resp.
O sinal negativo dei4 significa que o sentido adotado para 4 está incorreto e que 4, na verdade, está saindo do ponto P.
126
ELETRICIDADE BÁSICA
AS CORRENTES DE MALHA
Ás leis de kixchhoff podem ser simplificadas por meio de um método que utiliza as correntes de nwlha. Uma mc11w é qualquer percurso fechado de um circuito. Não importa se o percurso contém ou não uma fonte de tensão.
Ao resolver um circuito.utilizando as correntes de malha, temos que escolher previanxente quais os percursos que
formarão as malhas. A seguir, designamos uma corrente de malha para cada malha. Por conveniência, as correntes
de malha são geralmente indicadas no sentido horário. Este sentido E arbitrário, mas é o mais usado. Aplica-se en
tão a lei de kirchhoff para a tensão ao longo dos percursos de cada malha. As equações resultantes determinam as
correntes de malha desconhecidas. A partir dessas correntes, podem-se calcular a corrente ou a tensão de qualquer
resistor.
+
1’3
Figura 7-7 Um circuito com duas malhas.
Na Figura 7-7, temos um circuito com duas malhas denominadas de malhal e malha 2. A malhal é formada
pelo percurso abcda e a malhal é formada pelo percurso adefa. Todas as fontes de tensão e as resistências são
conhecidas. O procedimento para se determinar as correntes 4 e 4 das malhas do seguinte:
Passo 1: Depois de definir as malhas, mostre as correntes 4 e ‘2 das malhas no sentido horário. Indique a
polaridade da tensão em cada resistor, de acordo cora o sentido adotado para a corrente. Lembrese de que o fluxo convencional de corrente, num resistor, produz uma polaridade positiva onde a
corrente entra.
Passo 2: Aplique a lei de Kirchhoff para a tensão, ZV= 0, ao longo de cada malha. Percorra cada malha no
sentido da corrente de malha. Observe que há duas correntes diferentes (4,4) fluindo em sentidos
opostos, através do resistor li2, que é comum a ambas as malhas. Por esse motivo aparecem dois
conjuntos de polaridades para 1?, (Figura. 7-7). Percorra a malha 1 no sentido abcda.
+VA
2.
11R1
—
11i?2 + lzi?2
=
O
+VA—It(Rl +Rz)+12R10
+Ii(Ri+Rz)—12R2=V4
(1)
Observe que na primeira expressão I,fl2é positivo (+), pois passamos por uma queda de teusão do para o +.
Percorra a malha 2 no sentido adefa.
—
—12R2+11R2—12R3
—
l’j
=0
(2)
Observe que lI)?2 é uma queda de tensão positiva (-i-), pois passamos por uma queda de tensão
do — para o +.
-
Passo 3: Calcule 4 e 4, resolvendo as Equações (1) e (2) simultaneamente.
CAPtWLO 7
•
LEIS DE K1RCRHOFF
127
Passo 4: Quando as correntes de malha forem conhecidas, calcule todas as quedas de tensão nos resistores
utilizando a lei de Ohm.
Passo 5: Verifique a solução das correntes dc malha percorrendo a malha abcdefa.
VA
—
—
lzl?s
—
Vi
=
O
Exemplo 7.5
malha e as quedas de tensAo no circuito.
4
VÁ
=
55
=10V
11= lOA1
R2
4A
-4
b
a
a
(a)
(b)
=
6A
Figura 74 Determinação das correntes de malha e das quedas de tensão.
Passo 1:
Escolha as duas malhas conforme a indicação da figura. Indique a corrente da malha no senfido horário. Indi
que as polaridades em cada reBistor.
Pasao2:
ApliqueZV=0~sma1ha~ 1 ~
Malha l,t2bcda:
+58 —~ti ~ *312=0
(1)
+711—312=5S
Malba2,adefa:
3h —312—212
10=0
—
311—512=10
(2)
Observe que as correntes l~ e ‘2 das malhas passam aftavés de I?2, o resistor comum a ambas.
Passo 3:
Calculei, e 4, resolvendo as Equações (1) e (2) simultaneamente.
7h
—
~
=
58
-
311—512=10
(1)
(2)
Multiplicando a Equação (1) por 5 e a Equação (2) por3 obtêm-se as Equações (la) e (2a). A seguir, subtrai-se
a Equação (2a) da Equação (la).
3511—1512=290
(Ia)
~‘i —1512= 30
(2a)
h=1OA
.‘~.
128
EL2TRICIDADE BÁsicA
/
Substituindo 1~ = lOA na Equação (1), obtêm-se 1~.
711—312=58
7(10)—31a=S8
—31z~58—70
Resp.
A corrente através do ramo da é
1da11l2l046A
Resp.
Nesta caso, o sentido adotado para a corrente da malha estava correto, porque os valores das correntes são positivos.
Se os valores das correntes fossem negativos, o sentido verdadeiro seria o oposto ao sentido adotado para a corrente (veja
a Figura 7-81’).
Passo 4:
Calcule todas as quedas de tensão.
V1=11R1=l0(4)=40V
=
(li
—
12)l?2
=
6(3)
=
V3=12R3=4(2)=SV
Passo 5:
Rnp.
18V
kesp.
Resp.
Verifique a solução obtida para a corrente da malim percorrendo o laço abedefa e aplicando a lei de Kircbhoff
para tensão.
VA—Vl—VS—VR—— O
58—40—8—10
=
O
58—58=0
00
Vénficado
TENSÕES DOS NÓS
Outro método para resolver um circuito com correntes de malhas utiliza as quedas de tensão para determinar as
correntes em um nó. Escreve-se, então, as eguaçóes dos nós para as correntes, de forma a satisfazer a lei de Kirch
hoff para a corrente. Resolvendo as equações dos nós, podemos calcular as tensões desconhecidas dos nós. Um nó
é uma conexão comum a dois ou mais componentes. Um nó principal possui três ou mais conexões. Num circuito,
associa-se uma letra ou um número a cada nó. A, 8, O e N são nós, sendo O e N nós principais ou junções (Figura
7-9). Uma tensão de nó é a tensão de um determinado nó com relação a um nó em particular, denominado de nó
de referência. Escolha o nó G conectado ao terra, ou chassi, como o nó de referência. Então, VÂQ é a tensão entre
os nósA eG, V~éatensãoentreosnós8e (3, e V,~éatensãoentxtosnósNeG. Comoatensãodonóésempre
determinada em relação a um detenninado nó de referência, as notações V4, V~ e V~ são usadas para substitufrem
V,~, V~ e V,~, respectivamente.
Com exceção do nó de referência, pode-se escrever equações que usam a lei de lCiichhoff para corrente em
cada nó principal. Logo, o número de equações necessárias é igual ao número de nós principais menos 1. Como o
circuito apresentado (Figura 7-9) contém dois nós principais (N e G), precisamos escrever somente uma equação
para o nó N, a tini de calcular todas as quedas de tensão e as correntes do circuito.
-j
Cn’twLo 7
A
N
_Rs+
?
•
LEIS DE KlnctIHoF~
129
8
•lVb
,i
+
E
+
~-
‘1~”
Malhal
Malhal
Figure 7-9 Os nós num elreultocom duas malhas.
Considere que as correntes nos ramos I~ e 12 entram no nó N e que 4 saia do nó N (Figura 7-9). A escolha do
sentido das correntes 6 arbitrária. A partir da lei de Kircbhoff para corrente,
ti =0
r
11
+ 1213
=
O
13
=
11 + l~
(1)
Pela lei de Ohm,
13=—
(la)
—
1’,’
(1h)
—
(lc)
1?3
Substituindo essas expressões na Equação (1),
Vp,r
=
—
V~ + 1’~
—
(2)
Ri
Se VA, V~, R1, R2e 1?~ forem conhecidos, V~,pode ser calculado a partir da Equação (2). Assim, todas as quedas
de tensão e as correntes do circuito podem ser determinadas.
Exemplo 7.6 O circuito da Figura 7-8 (Exemplo7.5) resolvido pelo m&odo das correntes nos ramos está redesenhado
na Figura 7-10. Resolva por meio da análise das tens6es nodais.
Passo 1:
Adote o sentido das correntes conforme mostrado na Figura 7-10. Indique os nós A, li, Me G. Identifique a
polaridade da tensão em cada resistor de acordo com o sentido considerado para a corrente.
Passo2:
ApliqueaLKCaonóprincipalNeresolvaasequaçõesparaobter
13
13 + ~2
~M
130
ElErnIcIop.OE BÁSICA
A
~R1_
~
8
-
vI___>
<~_v3
4
40
20
+
+
r~=sgv
~v3=1ov
‘3
Malhal
o
Mallia2
nodais para o mesmo circuito da Figura 7-8.
Figura 740 Análise das tensões
~N
~
VA—Vj,r
—~=
+
V3—VN
58— VN + 1O—VN
4
2
3
Elimine as fraçôes multiplicando cada termo por li
4Vg=3(58—VN)+~Ø(l0— VN)
4~N= 174—3Vp,r+60—6Vji
‘3~N
VN
Passa 3:
=234
=
18V
Calcule todas as quedas de wnslio e as correntes.
V1=V4—Vjy=58—1840V
YZzVN=l8V
Resp.
Resp.
V3Vj~-Vjq~zl0—l&—8V
Resp.
O valor negativo de V, indica que 4 flui no sentido oposto ao sentido adotado e a polaiidade de V3 é o inverso
dos sinais mostrados em R3 (Figura 7-10).
V1
40
11y-4-lOA
Resp.
V3
—8
12=—=—=—4A
R3
2
Resp.
13=11+12=10—4=6A
R2
3
Resp.
Wr~flcar
Todos os valores calculados concordam cornos do Exemplo 7.5.
CAPtruLo
7
•
LEIS DE KIRCHHOFF
131
Problemas Resolvidos
7.1 Determine os sinais das tens~es ao se percorrer a malha afedcl’a e escreva as expressõeà para a LKT (Figu
ra7-ll).
1’
+ “e
-
VI
+
1’Á
v
.3
Figura 7-11 Percorrendo duas malhas.
Considere que os sentidos das correntes sejam os indicados. Marque as polaridades em cada resistor.
TI, é pois atravessamos uma queda & tensão do + para o
V~ 6— pois passamos por um aumento de tensão do + para o
V2 é pois passamos por uma queda de tensão do + para o-.
~ é pois atravessamos um aumento de tensão do ÷ para o—.
V~ é + pois atravessamos um aumento de tensão do para 0+.
I~1 é pois passamos por uma queda de tensão do + para o—.
—
—.
—.
-
—
—
—
—1’,
—
Vc
(VA
—
—
V2
Vc)
—
—
VB + VÁ
—
(TI1 ÷ 1— TI3)
=
o
=
O
=
O
Elevações dc tensão Quedas & tensão
Resp.
IS Calculei, e 14 (Figura 7-12).
b
a
+1
v
-÷
-*
I+30A
14r?
~:2Ajhi~0Aj
1
Figura 742 Determinação das correntes pela LKC.
--a
132
ELEmICIoADE BÁSICA
ApllqueaLKC, ZI=Oaonóa.
30
—
12— 14 = O
14=30—L2=ISA
Resp.
Aplique a LKC, EI = O ao nó b.
18—10—13=0
l3=18—108A
Resp.
Verifique a soluçEo.
IT=lL+12+13
30=12+10+8
30=30
Ve*ado
73 Calcule todas as correntes nas malhas paraocircuito de duas malhas mostado na Figura 7-13.
50
=
85
a
Figura 7-13 Duas malhas com uma fonte de tensão no ramo central.
Passo 1:
Indique as correntes nas malhas no sentido horúrio.
Passo2:
ApliqueZV=Oparaasmalhasle2ecorracadamalha.aPartirdea.flOSenüdOdaCOrItflW
da malta.
Malhal:
1011 =40
lj=4~
MalhnZ:
45—512=0
)~=9A
Passo 3:
Resp.
Rerp.
Faça a verificação percorrendo os laços nas malhas 1 e 2 aplicando EV= O.
VA—ILRI—I2RZ=0
85—4(10)—9(5)=0
85
—
40—45
O
85—85
O
Verificado
CAPÍTULO? • LEIS DE KIRCHHOFF
133
7.4 Calcule todas as correntes de malha e as quedas de tensão para o circuito de duas malhas mostrado na Fi
gura 7-14.
d
I~4
-
113
110v
b
1
a
Figura 7-14 Duas malhas com uma tente de tensão e uni resislor no ramo central.
Passo 1:
Mostre o sentido das correntes de malha conforme indicado.
Passo 2:
Aplique ZV=0 panas malhas 1 e 2, no sentido da corrente em cada nialha.
Malha l,abc&z:
I1O—Sl~ —190—511+512=0
(1)
—1011+512—80=0
—lOIi+SIz=80
Malha2,adefiz:
511—512+190—1512—2012=0
(2)
511—4022= —190
Passo 3:
Calcule I~ e I~, resolvendo as Equaç~es (1) e (2) simultaneamente.
—1011+512=
511 —4012
=
80
(1)
—190
(2)
Multiplique a Equaç~o (2) por 2paia obter a Equaçâo (2a); em seguida linplemente a soma.
—10/1+ 512=80
tplt
—.
8012
=
(1)
—380
(2a)
O
/ 300
/
12\~=4A
Resp.
Substitna4=4AnaEquaçâo(1)paracalcularj.
—lOIi-j-5(4)=8O
—lOli=60
11=—6A
Resp.
O sinal negativo significa que o sentido çonsiderado para 1~ nAo estava correto. Na reaiidade, o sentido de
.i~ é o anti-horário. No ramo 4411 ei, estão no mesmo sentido.
134
ELErHIQIOPJ)E 645 LOA
Portanto,
icidIl+12=6+410Ã
Passo 4:
Rexp.
Calcule as quedas de tensão.
Vi=JjRj=6(5)=30V
Vi
Passo 5:
=
(Ii+h)Ri
=
l0(~)
Resp.
50V
=
Resp.
Va=12R3=4G5)=60V
Resp.
V4=IiR~=4(20)8OV
Resp.
Faça a verificação. Percorra o laço abedefa (ntilize o sentido considerado inicialmente para ‘~
e
+VA
—
121?3
—
0
=
—
110— (—6)(5) —4(15) —4(20) =0
110 + 30—60 —80
O
=
140-140=0
7.5 Calcule a tensão V2 em
A
ç
%, pelo método da análise da tensão nodal (Figura 7-14a).
÷Rj_
a
~
w..
1~3
e—’E~
V1__+
—
—
20
+
J~=12V~
E
,—
1
+1
1
Verificado
20
20
+
—
6V
(a) Esquema do circuito
(b) Percurso fechado 030
Figura 745 Determinação de 1’2
pelo método da tensâo nodal,
Passo 1:
Considere o sentido mosuado para as correntes. Maique as polaridades da tensão. Indique os
nós A, 8, N, G.
Passo 2:
Aplique EI = O ao nó principal N.
(1)
13=11+12
Ví.
(la)
Vj
VA—VU
12—~N
8
1’3
I2i=
VB-.VN
Ã~
(lb)
V3—Vu
(Ic)
C~to7
•
~SDEKIRCKHO~
135
incapazes
Somos
de determinar l’3 pela simples an~iise da Equação (lc), porque a queda de
tensão 1’4 não é dada (Figura 7-15a). Portaiito, utilizamos a LKT para determinar V~ percorren
do o circuito completo de O a B, no sentido & ‘2 (Figura 7-15b).GBG constitui um percurso
completo, porque 1’8 é a tensão em E com relação ao terra.
F
—6—212—V8=Q
=
6
—
212
Substitua a expressão para 1!~ na Equação (lc),
12—
—6—212—Vw
a partir da qual obtemos
1:
12=
6
Substituaastrêsexpress&sparaconentenaEquaçâo(l).
Vjql2—V4y
—6—Vg
8
+
6
(2)
Agora a Equação (2) tem uma variável desconhecida, Ti,,,.
Passo 3:
Calcule
‘2
(V2= VN). Multipliquecada termo da Equação (2) por 24.
I2VN =(36—3Vpi)+(—24—4Ypj)
12
VN=C—=0,632V
19
=
0,632V
Resp.
7.6 ~
va as equações.
~-2Ü
40
60.
í~>vH~
20V--
30
~5O
r5V
+
-
Maibal
Malhs2
Malha3
flgura 7-16 Uni circuito com três malhas.
Indique as correntes de malha no sentido horário. Percorra os laços no sentido adotado para a corrente,
usandoaLKr,ZV=0.
Malhal:
Malha2:
MalhaS:
20—211—311+312=0
—412—512+513—312+311=0
—613+5—513-f-512=O
(1)
(2)
(3)
136
EIrHI0IDADE BÁSICA
Combine e rearranje os termos em cada equaçâo.
Malha 1:
Malha 2:
Malha3:
(la)
20 = 5I~ ~
Resp.
O = 31L + 1212 —513
—
5——512+tl1a
(2a1
Resp.
(3a)
Resp.
Um conjunto de qualquer número de equações simultineas, para um número qualquer de malha, pode
ser resolvido utilizando-se detentinantes. Este procedimento 6 apresentado no Capítulo 8.
Problemas Complementares
7.7 Calcule os valores desconhecidos indicados na Fig. 7-17 (a) e (b).
Résp. (a)1=8A; (b)VB=1OV
2V
20V~
1v~
1
1
6V
(2’)
(a)
Figura 7-17
~Ca1cu1e a corrente e as quedas de tensão em E1 eR1 (Figura 7-18).
Resp.
1=IA;
V4=1OV;
Y220V
‘-À-A.
200
VÁ
n
10V
40
15V
_iIiI+
‘tA
1111
100
4OVT
+
=
20 V
Figúra 748
60
=50V
~0~
—
115 V
Figura 7-19
7.9 Uma corrente de 6 A percorre o circuito visto na Figura 7-19. Calcule o valor deR.
e
Resp.
R=5fl
Calcule 1»13 t V~ (Figura 7-20).
Resp. i2=6A;13=2Afl’~=152V
7.11 Calcule as correntes de malhal1 e 4 e todas as quedas de tensão pelo método das correntes de malha (FigaIa 7-21).
Resp.
11=5A;12=3A;Y1=30V;V2=30V;V3=60V;V4=6V;V3=9V;V6=15V
CAi’fruLo7
•
LEIS DE KlRcIlHoFr
60
=
20
13
8 A
40
30
420 V
200
+
600
‘l~i2
VAL
120
Figura 7-20
3.
cl
137
59
Figura 7-21
Calcule todas as correntes nas resistências pelo método da corrente dc malha (Figura 7-22).
Rexp. i,=3A;12~. 1A;11—12n2A(fluindodeaparab)
40
.4-
a
[r~
25V..
19
a
29
50
-
40
3
4,
~60
:20
+
4,
iOV~
10V
‘A,__
10
b
30
15
J
Sgura 7-22
Figura 7-23
(~j) Resp.
Calcule a corrente em cada resistor, utilizando o método da corrente de malha (Figura 7-23).
1, 2 A; 1, —1 A (o sentido considerado para a contate inicialmente estava incorreto), ou 1, 1 A no sentido
=
=
=
anti-horário; 1, + 4 = 3 A (fluindo de a para 15).
7.14 Calcule as correntes 4 e
7-24).
e a corrente na bateria de 20 V, usando o método da cOrreflte de malha (Figura
Resp. 1,=2A;4=5k4—4=3A(fluindodebpaxaa).
7.15 Calcule as correntes I~ e e a corrente no resistor em série com a bateria de 20V (Figura 7-25). Utilize o
método da cormnte de malha.
Resp. 1, —0,1 A; 4 -l A (o sentido considerado para a corrente inicialmentc estava incorreto. Na realidade, o
sentido dei, é o anti-horário); ~2 = 0,7 A 1, + 4 = 0,8 A (fluindo dei’ para a).
7.16 Calcule as correntes 4 ~ 4 e a corrente no resistor de 20 Ç2 comum às malhas 1 e 2 (Figura 7-26). Aplique
o método da corrente de malha.
Resp. 11=O.6A;4=0,4A;12—ij=0,2A(fluindodcaparab).
7.17 Calcule rodas as correntes e as quedas de tensAo pelo método da corrente de malha. (Figura 7-27).
Resp.
4=6A;1,=7A;l2—4=IA(fluindodebparaa).
In
21
138
Etanic IDADE BÁSICA
300
40
10 O
a
100
1’
li
Figura 7-24
Figura 7-25
a
15Q
30
a
+
200
20V
28
1’
10
b
Figura 7-26
Figura 7-27
7.18 Calcule todas as correntes e as quedas de tensão pelo método da análise de tensão nodal (Figura 7-28).
Resp.
I3=5A;I_lA(emopsiç~OaoSeS1tk1OI1105d0);I,4I2=24~~3\’
7.19 Utilizando o método da tensão nodal, calcule todas as correntes e as quedas de tensão (Figura 7-29).
Resp. j,1,42A;J _1,1OA(cmoposiÇAOaOSenfldOmOSft2il0)a3~,32k V,IIAV; ~O,64V V,2,2V
¼ = 4A V
80
•-_~
~_-_
11
2O
‘2
40
4
.4.
v
MV
20
l2V-~
v
1
Figura 7-28
Figura 7-29
CAP11ULO 7 • LEIS DE KRCF*-IOFF
139
Escreva as equações das malhas para o circuito mostrado na Figura 7-30. Não resolva as equações.
Resp.
6I3—24=i0;—2L+812—2t3=O;_2I1+6i~-.4
20
20
v
10V
20
20
20
Figura 740
7.21 Verifique os valores das correntes no circuito da Figura 7-23 (Problema 7.13) pelo método da tensão nodal.
7.22 Verifique os valores das correntes no circuito da Figura 7-25 (Problema 7:15) pelo método da tensão nodal.
7.23 Calcule os valores de todas as correntes
e indique os respectivos sentidos no nó N
(Figura 7-31). (Sugestão: V~= 1,67V)
Resp.
O,94A N
1~
0,83 A
15 O
O,IIA
ti
:150
5 O
200
+
30Ve
r
ioe
r15V
+
G
Figura 7-31
7.24 Se o resistor de 20 Q (Figura 7-31) for substituído por um resistor de 30 fl, qual será a tens~.o nodal ‘/~?
Resp.
V=3,75V