Lista de exercícios – PRA

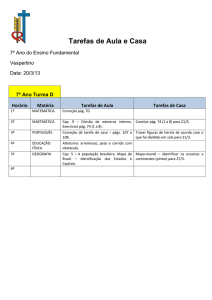
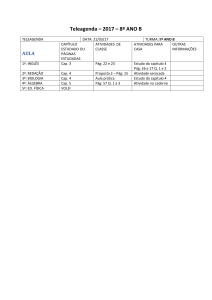
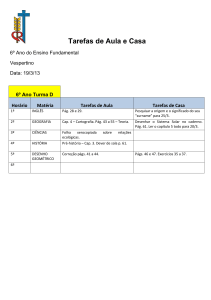
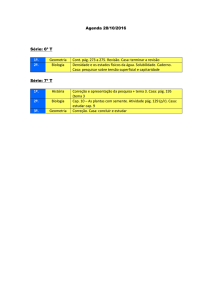
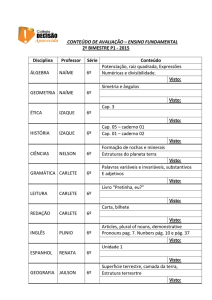
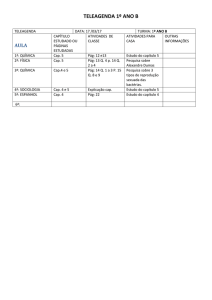
Lista de Exercícios- PRA
Física Geral Experimental I
I – Velocidade Média:
1 - Um avião vai de São Paulo a Recife, em 1 h 40. A distância entre as cidades é
aproximadamente 3 000km. Qual a velocidade média do avião.
R- 5.102 m/s
2 - Um carro percorreu 20 km com velocidade média de 60 km/h e 60 km a 90 km/h.
Determine a velocidade escalar média do carro nos 80 km percorridos.
R - 80 km/h = 22,22 m/s
3 - (Cap. 2 Ex 50 Tipler) Um veículo se movimenta em linha reta com uma velocidade média
de 80 km/h durante 2,5 h e, em seguida, com uma velocidade média de 40 km/h durante 1,5
h.
a) Qual é o deslocamento total do período de 4 h de percurso?
b) Qual é a velocidade média de todo o percurso?
4 - Um automóvel percorre metade de sua trajetória com velocidade média de 70 km/h e a
outra metade com velocidade média de 90 km/h. Qual a sua velocidade média em todo
trajeto?
R - 78,75 km/h = 21,87m/s
5 - Uma patrulha rodoviária mede o tempo que cada veículo leva para percorrer um trecho de
400 m da estrada. Um automóvel percorre a primeira metade do trecho com velocidade de
140 km/h. Sendo de 80 km/h a velocidade limite permitida, qual deve ser a maior velocidade
média do carro na segunda metade do trecho para evitar ser multado?
R – 56 km/h = 15,56 m/s
II - Cinemática – MU:
1 - A equação horária do movimento de uma partícula é S(t) = 100 – 5.t (SI). a) Determine o
posição inicial e a velocidade da partícula. b) Classifique o movimento em progressivo ou
retrógrado. c) Qual a posição da partícula no instante t = 6 s? d) Em que instante a partícula passa
pela origem S = 0 m? e) Esboce os gráficos S(t)t.
2 - (Cap. 2 Ex 60 Tipler) Dois carros estão se movendo ao longo de uma estrada. O carro A
mantém uma velocidade constante de 80 km/h; o carro B mantém uma velocidade constante
de 110 km/h. No tempo t = 0, o carro B está 45 km atrás do carro A. Que distância o carro A
deve percorrer antes de ser ultrapassado pelo carro B?
R – 120 km = 120 000 m
3 - O gráfico mostra a posição (S), em função do tempo (t), de
dois automóveis, A e B. Determine:
a) As velocidades dos automóveis.
b) As funções horárias da posição em relação ao tempo.
4 - Dois móveis, A e B, percorrem a mesma trajetória retilínea. A figura representa as posições (s),
dadas em metros, em função do tempo (t), dado em segundos,
desses dois móveis. No instante t = 5 s, qual a distância entre
ambos?
R - 5,5 m
III – Cinemática – MUV:
1 - (Cap. 2 Ex 71 Tipler) Um carro em repouso na coordenada x = 50 m acelera a uma taxa
constante de 8 m/s2.
a) Qual é sua velocidade após 10 s?
b) Qual é a distância percorrida após 10 s?
c) Qual é sua velocidade média no intervalo O ≤t ≤10 s?
2 - Quando a luz verde de um sinal de trânsito acende, um carro parte com aceleração constante a =
2,2 m/s2. No mesmo instante, um caminhão, com velocidade constante de 9,5 m/s, ultrapassa o
automóvel, (Fundamentos de Física - Mecânica, capítulos 2, Vol. 1, D. Halliday, R. Resnick, J.
Walker)
a) A que distância, após o sinal, o carro ultrapassará o caminhão?
b) Qual a velocidade do carro nesse instante?
3 - (Ex 2.28 - Física - Mecânica, capítulos 2, Vol. 1, Sears e Zemansky)Um trem de metrô parte
do repouso em uma estação e acelera com uma taxa constante de 1,60 m/s2 durante 14,0 s. Ele viaja
com velocidade constante durante 70,0 s e reduz a velocidade com uma taxa constante de 3,50 m/s2
até parar na estação seguinte. Calcule a distância total percorrida.
4 - (Cap. 2 Ex 75 Tipler) Uma bola é lançada para cima com uma velocidade inicial de 20
m/s.
a) Durante quanto tempo a bola permanece no ar?
b) Qual é a maior altura atingida pela bola?
c) Quanto tempo após o lançamento a bola estará 15 m acima do ponto em que foi lançada?
5 - Um tijolo é largado (velocidade inicial nula) do alto de um edifício. Ele atinge o solo em 2,50 s.
A resistência do ar pode ser desprezada, de modo que o tijolo está em queda livre. (Ex 2.36 - Física
- Mecânica, capítulos 2, Vol. 1, Sears e Zemansky)
a) Qual é a altura do edifício?
b) Qual é o módulo da velocidade quando ele atinge o solo?
6 - Ex. 44 - Cap 2, pág 63, Física - Mecânica, Sears e Zemansky, 12a ed Um balonista de ar
quente que se desloca verticalmente para cima com velocidade constante de módulo igual a 5,0
m/s deixa cair um saco de areia no momento em que ele está a uma distância de 40,0 m acima
do solo. Depois que ele é largado, o saco de areia passa a se mover em queda livre.
a) Calcule a posição e a velocidade do saco de areia 1,00 s depois que ele é largado.
b) Calcule o tempo que o saco de areia leva para atingir o solo desde o momento em que ele
foi lançado.
c) Qual é a velocidade do saco de areia quando ele atinge o solo?
d) Qual é a altura máxima em relação ao solo atingida pelo saco de areia?
R - a) 40,3 m b) 3,15 s c) 41,27 m
7 - ( Tipler - Ex 103 Pg 53 ) Um avião, pousando em uma pequena ilha tropical, dispõe de
exatamente 70 m de pista para parar. Se sua velocidade inicial é de 60 m/s:
a) Qual deve ser a menor aceleração do avião durante a aterrissagem, admitindo que seja
constante?
b) qual o tempo necessário para o avião parar com essa aceleração?
8. (Ex 75, pág 52, Tipler 5a Ed) - (Ex 69, pág 57, Tipler 6a Ed) Uma bola é lançada para cima
com uma velocidade inicial de 20 m/s. a) Durante quanto tempo a bola permanece no ar? b) Qual é
a maior altura atingida pela bola? c) Quanto tempo após o lançamento a bola estará 15 m acima do
ponto em que foi lançada?
9 - Um construtor está em cima de uma laje, a uma altura de 5 m. Ele está recebendo blocos
de concreto manualmente, de um colega de trabalho, que joga verticalmente até ele.
Pergunta-se:
a) Qual deve ser a velocidade inicial, que o colega deve lançar este bloco, para que o
construtor o receba?
b) Qual o tempo de permanência do bloco no ar até chegar ao construtor?
10. No instante t = 0, a posição de um móvel é S0 = 10 m. A velocidade escalar em função do tempo
é representada pelo gráfico abaixo. Qual a posição do móvel no instante t = 4s?
V(m/s)
20
4
0
t(s)
IV – Vetores, Soma de vetores e Sistema de coordenadas:
1 - (R. C Hibbeler – Mecânica - Estática –exemplo 2.6
p.28) O elo mostrado na figura abaixo está sujeito a duas
forças F1 e F2. Determine o módulo da força resultante,
utilizando a lei dos cossenos.
R – F = 629,07 N
2 (Sears 10ªed cap 1 ex 33 ) Determine as componentes x e y dos vetores A, B e C indicados na
figura abaixo e calcule o vetor resultante.
3 - (Cap 1 Exemplo 1.9 pág 18 - 6a ed Tipler) Você está trabalhando em um resort tropical, e
está preparando urna atividade de caça ao tesouro para os hóspedes. Você recebeu um mapa e
instruções para seguir suas indicações e enterrar um "tesouro" em dado local. Você não quer perder
tempo caminhando pela ilha, porque precisa concluir logo a tarefa para ir surfar. As indicações são
as de caminhar 3,00 km apontando para 60,0° nordeste, e depois 4,00 km apontando para 45,0° a
noroeste. Para onde você deve apontar e quanto deve caminhar para concluir rapidamente a tarefa?
Encontre a resposta graficamente e usando componentes.
4 - (Resnick 5ªed cap 2 ex 12) Um carro é dirigido para o leste por uma distância de 54 km e,
então, para norte por mais 32 km e, finalmente, para uma direção 28º a noroeste por 27 km.
Desenhe o diagrama de vetores e determine o deslocamento total do carro a partir de seu ponto de
partida.
V - Cinemática vetorial:
1 - (Cap. 3 Ex 53 pág 88 Tipler 5 a ed – Ex 45 pág 86 6a ed) Um operador de radar
estacionário indica que um navio esta a 10 km na direção sul. Uma hora mais tarde o mesmo
navio esta 20 km na direção 45° sudeste. Se o navio se move com velocidade constante e
sempre na mesma direção, qual foi sua velocidade durante esse tempo em m/s? R: V = (3,93i
- 1,15j) m/s.
2 - (Cap. 3 Ex 55 pág 88 Tipler 5 a ed – Ex 47 pág 86 6a ed) Uma partícula movendo-se com
uma velocidade de 4,0 m/s no sentido positivo do eixo x e dada uma aceleração de 3,0 m/s 2
no sentido positivo do eixo y durante 2,0 s. Qual a velocidade final da partícula? R: V = (4i +
6j) m/s.
3 - Num instante t1, um carro de Fórmula 1 encontra-se a 600 m ao norte em
relação ao box de sua equipe, e 20s depois a 800 m a oeste do mesmo

referencial. Determinar a velocidade vetorial média do carro ( V méd ), seu
módulo, sua direção e sentido entre esses dois instantes.
4 - (Cap 3 Ex 61 Tipler pág 88 Tipler 5a ed – Ex 53 pág 86 6a ed) Partindo do repouso em
uma doca, um bote a motor orientado para o norte
e submetido a uma aceleração constante 3 m/s 2
durante 20 s. Em seguida, o bote se vira para oeste
com a velocidade que possuía no tempo de 20 s e
se move orientado para o oeste com essa
velocidade constante durante 10 s. a) Qual é o
deslocamento do bote desde a doca ate o final de
seu percurso de 30 s? b) Qual foi a velocidade
média do bote durante os 30 s de seu percurso?
R: a) r = (-600i + 600j) m, b) V M= (-20i + 20j) m/s.
VI - Movimento de um Projétil:
1 (Cap. 3 Ex 86 pág 89 Tipler 5a ed –Ex 82 pág 88 6a ed) Um canhão e elevado a um angulo
de 45°. Ele atira a munição com uma velocidade de 300 m/ s. Para
todos o problemas desta lista, use g=9,81 m/s2.
a) Qual e a altura atingida pela munição?
b) Quanto tempo a munição permanece no ar?
c) Qual e o alcance horizontal do canhão?
R: a) h= 2,29 km b) t = 43,2 s c) x = 9,16 km.
2 (Halliday Cap 4 Ex 26 pág 86) Uma pedra é lançada em um rochedo de altura h com uma
velocidade inicial de 42,0 m/s e um ângulo o = 60,0°
com a horizontal. A pedra cai em um ponto A, 5,5 s após
o lançamento. Determine:
a) a altura h do rochedo,
b) a o módulo da velocidade V da pedra imediatamente
antes do impacto no ponto A.
c) a máxima altura H alcançada acima do solo.
R: a) h= 51,66m b) v = 27,39 m/s c) H = 67,42 m.
3 (Cap 4 Exemplo 4-6 Halliday pág 74) Um avião de salvamento voa a 198 km/h, a uma
altura constante de 500 m, rumo a um ponto diretamente acima da vítima de um naufrágio,
para deixar cair uma balsa.
a) Qual deve ser o ângulo  da linha de visada do piloto para a vítima no
instante em que o piloto deixa cair a balsa?
a) No momento que a balsa atinge a água, qual é sua velocidade V em
termos dos vetores unitários e na notação módulo-ângulo
R: a) = 48º b) V = (55 m/s)i - (99 m/s)j, |V| = 113 m/s ,  = -60,9º.
4 (Cap. 3 Ex 87 pág 89 Tipler 5a ed –Ex 83 pág 88 6a ed) Uma pedra lançada
horizontalmente do topo de uma torre de 24 m atinge o solo em um ponto a 18 m de sua base.
a) Obtenha a velocidade com a qual a pedra foi lançada.
b) Determine a velocidade da pedra no instante imediatamente anterior ao seu impacto com o
solo.
R: a) |V0| = 8,14 m/s b) V = (8,14 m/s)i - (21,7 m/s)j.
5 (Extra) Uma partícula é lançada com velocidade horizontal de
módulo é vo = 20 m/s, de um ponto O situado a 100 m acima do
solo. A partícula atinge um muro vertical, situado a 80 m do ponto
O. Determine a altura h do ponto B (S y) onde a partícula atinge o
muro. (Despreze os efeitos do ar.)
R: h= 21,52 m.
Sy = ?
100 m
80 m
6 - (Cap. 3 Ex 91 pág 90 Tipler 5a ed) A munição de um canhão e lançada com uma
velocidade inicial de 42,2 m/s a um ângulo de 30° acima da horizontal, de uma altura inicial de
40 m. Determine o alcance da munição.
R: S= 209m.
7 - (Cap. 3 Ex 90 pág 90 Tipler 5a ed) Um projétil e lançado a um ângulo de 60° acima da
horizontal com uma velocidade inicial de 300 m/ s. Calcule: a) a distancia horizontal
percorrida; b) a altura vertical atingida nos primeiros 6s do percurso.
R: a) S= 7945,2m b) h = 1364,3 m.