Aula3_Ondas_III

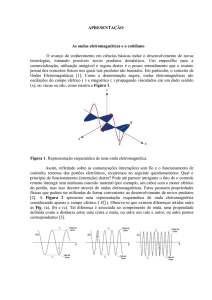
Aula 3
Ondas Eletromagnéticas
- Luz visível (nos permitem ver)
- Infravermelhos (aquecem a Terra)
- Ondas de radiofrequencia (transmissão de
rádio)
- Microondas (cozinhar)
-Transporte de momento linear
- Polarização e Polarizadores
- Reflexão e Refração
- Dispersão
- Polarização por Reflexão
Ondas Longas
Ondas de Radio
microondas
Infravermelho
Ultravioleta
Raios-X
Raios Gama
Ondas Eletromagnéticas
• São ondas transversais
• Os campos elétricos e magnéticos de uma onda
eletromagnética plana são perpendiculares entre si
e à direção de propagação.
• Não necessitam de meio para propagar.
• Obedecem o princípio da superposição pois as
Equações Diferenciais para E e B são lineares
Características de uma onda
eletromagnética
Velocidade de propagação
No vácuo
1
c
00
1
Em meios materiais v 
με
t  3t
t  2t
t  t
t
cv
Em geral

v( r ) 
1
 
(r )(r )
frentes de
onda
raios
A equação de onda
A equação da onda eletromagnética
• Em geral, qualquer função periódica pode ser solução de uma
equação de onda pois poderá ser expressa por uma Série de
Fourier
Ondas eletromagnéticas
(3ª Eq. de Maxwell)
Bz transverso à direção
de propagação da onda:
• Sejam:
E y ( x, t )  Em sen(kx  t ) e Bz ( x, t )  Bm sen(kx  t )
Em 
 c
Bm k

Ey
Bz
c
c
1
0 0
Ou seja, a todo instante a razão entre o
campo elétrico e o campo de uma onda
eletromagnética é igual á velocidade da
luz.
Ondas eletromagnéticas planas
E y ( x, t )  E0 sin k ( x  ct )  E0 sin( kx  t ) ;   ck
Direção de
deslocamento da
onda
Frente de onda plana
A frente de onda é o lugar geométrico dos pontos onde
 
k  r  t  const.
Ondas eletromagnéticas –
principais parâmetros
Período:
T
Comprimento
de onda:
Freqüência:
1
f 
T
Freqüência
angular:
Número
de onda:
k
2

Velocidade
de uma onda:

  2 f
v

k
f
Geração de Ondas eletromagnéticas
transformador
oscilador
L
~
Geração de Ondas eletromagnéticas
O oscilador está acoplado a uma linha de transmissão por um transformador.
Este acoplamento gera uma corrente no oscilador que varia
senoidalmente e provova uma oscilação das cargas do
oscilador com frequencia =(LC)1/2.
A antena equivale a um dipolo elétrico cujo momento dipolar
elétrico varia com o tempo.
 ~ 1m,
Ondas de rádio
Transporte de Energia por ondas
eletromagnéticas
As densidades de energia elétrica e magnética são:

1
uE ( r , t )   0 E 2
2
como
E
B
c

e
2

B
uB ( r , t ) 
20
2

E
1
uB ( r , t )  2   0 E 2
2c 0 2
Logo, a densidade total de energia armazenada no campo
de radiação é:



u ( r , t )  uE ( r , t )  uB ( r , t )   0 E 2



u ( r , t )  uE ( r , t )  uB ( r , t )   0 E 2
 

2
2
E (r , t )  E0 sin (k  r   t )
Como
2
A média temporal da densidade de energia é dada por :
T
u  0 E
2
  0 E02
 
1
1
2
sin ( k  r   t ) dt   0 E02
T0
2





1
2
A intensidade da radiação será então:
U
U 
1
2
I

 u c  c 0 E0
A t A  t
2
Pode-se desenvolver a mesma expressão como:

  E02

2
EB 
sin ( k  r   t )k̂
c
Calculando-se a média temporal:
y
U

E0

ds
 
E02 1
2
| EB|
 c0 0 E0
2c 2

B0
z
  ct

k
x
A taxa de fluxo de energia é definida
então pelo Vetor de Poynting.
 1  
S  EB
0
A intensidade de uma onda eletromagnética é igual à
densidade média de energia multiplicada pela
velocidade da luz.
I  Smedio  c .umedia
Transporte de momento linear da onda
eletromagnética
Pressão de radiação
O mesmo elemento que transporta
a energia U também transporta o momento
linear
 U
p 
k̂
c
Momento linear transferido para um objeto onde
incide a radiação
 U ˆ
pa 
k
c
U ˆ

pr  2
k
c
no caso de absorção
total da radiação
no caso de reflexão
total da radiação

p

p

p
Mas,
U
I
A t
força
U  IA t
pressão

p
Pressão de
radiação na
absorção total
pa IA
Fa I
Fa 

 Pa  
t
c
A c
Pressão de
radiação na
reflexão total

p
pr 2 IA
Fr 2 I
Fr 

 Pr  

t
c
A c
p
força
pressão
Polarização da radiação
Polarização linear:
Direção do campo elétrico
 
E (r , t )
Polarização linear
 
 

E (r , t )  E0 sin( k  r   t )
Polarização circular
 
E (r , t )  E0 sin( kz   t ) xˆ
 E0 cos(kz   t ) yˆ


E x2 (r , t )  E y2 (r , t )  1
Polarização elíptica
Ey
 
E (r , t )  Ex 0 sin( kz   t ) xˆ  E y 0 cos(kz   t ) yˆ

2 
E (r , t ) E y (r , t )

1
2
2
Ex 0
Ey0
2
x
Um pulso eletromagnético geral corresponde a uma
superposição de vários pulsos que oscilam em
diferentes direções, com diferentes fases
radiação não-polarizada
Ex
Polarizadores
A luz polarizada em uma dada direção é absorvida pelo material
usado na fabricação do polarizador. A intensidade da luz
polarizada perpendicularmente a esta direção fica inalterada.
Exemplo:
Fios metálicos
Polarizadores
Intensidade da radiação incidente
não-polarizada:
Intensidade da radiação
polarizada ao longo de ŷ
1
I 0  c 0 E02
2
I0
I  I 0 cos  
2
2
2
I0
cos  d 
2
0

2

Luz não-polarizada
Luz polarizada
verticalmente
Luz polarizada
para um ângulo 

Filtro polarizadador vertical
Analisador – a luz incidente deve estar
polarizada
Intensidade incidente da
radiação polarizada:
E||  E0 cos 
E   E0 sin 
Intensidade da radiação
polarizada ao longo de :
I  I 0 cos 
2
1
1
2
I  c 0 E  c 0 E||2
2
2
Reflexão e refração: Princípio de Huygens
Todos os pontos de uma frente de onda se
comportam como fontes pontuais para ondas
secundárias.
Depois de um intervalo de tempo t, a nova posição
da frente onda é dada por uma superfície
tangente a estas ondas secundárias.
Índice de refração
c
n
v
v1
v2
Reflexão especular x Reflexão difusa
Lei de Snell
n1  n2
 2  1
n1
sen  2  sen 1
n2
n1  n2
 2  1
Reflexão interna total
Se a incidência se dá de um meio mais refringente para
outro menos refringente, ou seja, n1  n 2 , há um
ângulo crítico acima do qual só há reflexão.
n1 sin1  n2 sin2

n1 sin c  n 2 sin  n 2
2
1 n 2

c  sin  
 n1 
2
n2
n1
1
c
n1 > n2
Reflexão interna total:
fibras ópticas
Dispersão Cromática
n  n( )
n1 sin1  n2 sin2
Em geral, se 1  2  n(1 )  n(2 )
Luz branca
Para cada cor, 1 igual,
2 muda.
Dispersão cromática: Formação do arco-íris
~ 42º
Reflexão de ondas
transversais
Corda com uma extremidade fixa:
Pulso refletido invertido ao pulso incidente
Polarização por reflexão
A luz refletida por uma
superfície é totalmente
polarizada na direção
perpendicular ao plano de
incidência quando

i  re fr 
2
Então
Raio incidente
(não-polarizado)
n2
tan i 
n1
B r



 r  re fr  
2



n1 sin i  n 2 sin  i 
2

Raio refletido
(polarizado)
n1
n2
ref
Raio refratado
(fracamente
polarizado)
i  B  tan
B
1 n 2
n1
: ângulo de Brewster