4 – E

LISTA DE EXERCÍCIOS OPTATIVA 4 – ELETRICIDADE
Prof. Carlos E. VIANA
2o. Semestre de Tecnologia Mecânica – Ênfase em Mecatrônica
E x e r c í c i o 1 Você tem os seguintes resistores em mãos: 3 Ω, 5 Ω, 7 Ω, 9 Ω,
12 Ω, 15 Ω, 28 Ω, 60 Ω e 100 ΩPede-se:
a) Monte um circuito com resistência total de 19 Ω;
b) Monte um circuito com resistência total de 40 Ω;
c) Monte um circuito com resistência total de 55 Ω;
d) Monte um circuito com resistência total de 24 Ω;
e) Monte um circuito com resistência total de 37,5 Ω.
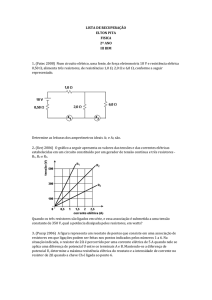
E x e r c í c i o 2 Observe os circuitos abaixo: Considere que R1 = 2 Ω, R2 = 6 Ω ,
R3 = 4 Ω e U = 60 V.
=
a) Determine o valor da resistência equivalente (Req), que poderia ser
usada em substituição às três resistências;
b) Calcule o valor da corrente elétrica que passa pelo circuito;
c) Indique no desenho o sentido convencional da corrente elétrica;
d) Indique o valor da corrente elétrica que passa em cada um dos
resistores;
e) Calcule U1 , U2 e U3 , ou seja, a diferença de potencial (d.d.p.) em
cada um dos resistores;
f) O que você pode esperar de U1 + U2 + U3 ?
E x e r c í c i o 3 Você tem três resistores ligados em série. A resistência de cada
um deles é de 3 Ω, 5 Ω e 2 Ω.
a) Desenhe estes três resistores "montados" em série em um circuito
que esteja ligado a uma bateria de 30V;
b) Qual o valor da resistência total do circuito (devido aos três
resistores)?
c) Qual o valor da corrente elétrica que circula neste circuito?
d) Qual o valor da corrente elétrica em cada um dos resistores?
e) Calcule o valor da d.d.p. em cada um dos resistores;
f) Calcule o valor da potência elétrica dissipada em cada resistor;
g) Calcule o valor da potência elétrica dissipada no circuito inteiro.
LISTA
DE
EXERCÍCIOS OPTATIVA 4 – ELETRICIDADE
- 1 -
E x e r c í c i o 4 Você
tem
os
seguintes
resistores
em
mãos:
1 Ω , 3 Ω , 5 Ω , 6 Ω. Desenhe um circuito que tenha resistência equivalente
igual a 2 Ω (Isto somente poderá ser feito ligando-se dois resistores em
paralelo).
E x e r c í c i o 5 Observe o circuito a seguir. Considere que R1 = 6 Ω, R2 = 12 Ω
e U = 60 V.
=
a) Determine o valor da resistência equivalente (Req), que poderia ser
usada em substituição às duas resistências;
b) Calcule o valor da corrente elétrica que passa pelo circuito;
c) Desenhe o circuito e indique o sentido convencional da corrente
elétrica;
d) O que você pode esperar da tensão no resistor 1 (U1) e da tensão
no resistor 2 (U2) , uma vez que eles estão ligados em paralelo ?
e) Indique o valor da corrente elétrica que passa em cada um dos dois
resistores;
f) O que você pode esperar da soma destes dois valores de corrente
(I1 + I2) ?
g) Calcule o valor da potência elétrica dissipada em cada resistor;
h) Calcule o valor da potência elétrica dissipada em todo o circuito.
E x e r c í c i o 6 Se os dois resistores do problema anterior fossem ligados em
série, quais seriam os valores de: Req, U1, U2, I1 e I2.
E x e r c í c i o 7 Do gráfico ao lado (“invertido”) podemos retirar várias
informações sobre um gerador. Pede-se:
a) Qual a d.d.p. "gerada" pelo gerador, também
conhecida como força eletromotriz (f.e.m.) ?
b) Qual o valor da corrente máxima que pode
ser "puxada" deste gerador por algum
aparelho ?
c) Qual é o valor da resistência interna deste
gerador ?
d) Qual e equação que representa este gerador?
e) Imaginando que a corrente que atravessa um aparelho que esteja
ligado a este gerador seja de 3 A, determine a d.d.p. oferecida pelo
gerador ao aparelho;
LISTA
DE
EXERCÍCIOS OPTATIVA 4 – ELETRICIDADE
- 2 -
f) Se o aparelho estiver submetido a uma d.d.p de 16 V, qual será o
valor da corrente que o atravessará ?
E x e r c í c i o 8 Um gerador possui f.e.m. igual a 60V, mas oferece a um
circuito externo uma d.d.p. de somente 20V. Sabemos que a resistência
interna deste gerador é de 5 Ω. Determine:
a) A equação deste gerador;
b) A corrente que atravessa o circuito.
E x e r c í c i o 1 6 Calcule a intensidade de corrente elétrica num circuito que
contém:
• Gerador 1: E1 = 4,0 V e r1 = 0,5 ohms;
• Gerador 2: E2 = 3,0 V e r2 = 0,5 ohms;
• Resistor 1: R1 = 5,0 ohms;
• Resistor 2: R2 = 3,0 ohms;
• Resistor 3: R3 = 2,0 ohms;
E x e r c í c i o 9 Determine as resistências equivalentes (Req) das associações
Todos os elementos estão ligados em série.
de resistores:
a) R1= 6Ω, R2 = 3Ω e
E x e r c í c i o 1 7 Um radinho de pilha funciona com seis pilhas, cada uma com
R3 = 2Ω.
b) R1=3Ω, R2=7Ω , R3=5Ω,
R5 = 2Ω
R4=6Ω e
a)
b)
E x e r c í c i o 1 0 Dê exemplos de alguns tipos de energia que você conhece.
E x e r c í c i o 1 1 Cite maneiras de transformar as energias citadas em energia
f.e.m. de 1,5 V e resistência interna de valor 0,2 ohms cada. Elas estão
dispostas em dois grupos associados em paralelo. Cada um desses grupos
contém 3 pilhas ligadas em série. Determine:
a) A resistência interna equivalente bem como a força eletromotriz
equivalente;
b) Faça o mesmo supondo as 6 pilhas ligadas em série;
c) Faça o mesmo supondo as 6 pilhas ligadas em paralelo.
do tipo elétrica.
E x e r c í c i o 1 8 Dado o circuito indicado na figura a seguir, pede-se calcular as
E x e r c í c i o 1 2 O que diferencia um gerador real de um gerador ideal ?
intensidades das correntes I1 , I2 e I3 .
E x e r c í c i o 1 3 Imagine um gerador que diz trabalhar
com tensão de 30V, e possuir resistência interna
de 5Ω. A "voltagem" que realmente será "sentida"
pelo circuito vai depender da corrente que o
atravessar, que por sua vez dependerá da Req do
circuito. Para as Req dadas, na tabela ao lado,
calcule a corrente (I) que o atravessará e a
respectiva "voltagem" (V) "sentida" pelo circuito.
Req (Ω
Ω)
I (A)
--
0
V (V)
25
10
5
1
0
E x e r c í c i o 1 4 Com os valores encontrados na questão anterior, construa um
gráfico V(V) x I(A). Depois interprete fisicamente os pontos onde o gráfico
cruza o eixo vertical e horizontal.
E x e r c í c i o 1 5 São três geradores ligados em paralelo, um deles tem f.e.m.
10 V. Encontre a f.e.m. dos outros dois, bem como o valor do gerador
equivalente.
LISTA
DE
EXERCÍCIOS OPTATIVA 4 – ELETRICIDADE
- 3 -
LISTA
DE
EXERCÍCIOS OPTATIVA 4 – ELETRICIDADE
- 4 -