I(R - Moodle @ FCT-UNL

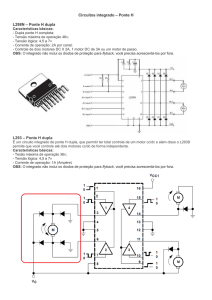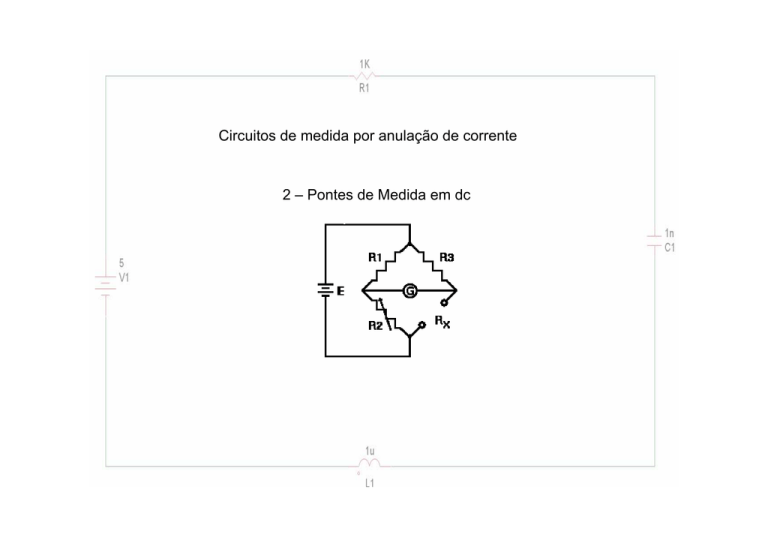
Circuitos de medida por anulação de corrente
2 – Pontes de Medida em dc
2.1 – Ponte de Wheatstone
A
R1
C
R2
D
G
Rx
R3
B
Se VAC = VAD então VCB = VDB e VCD = 0
Se VCB =0 então IG =0
-> Princípio de banceamento ou de equilíbrio (corrente nula)
A
2.1 – Ponte de Wheatstone
R1
C
Nestas condições,
R2
D
G
Rx
R3
VAC = I(R1).R1 = VAD = I(R2).R2
B
VCB = I(R3).R3 = VDB = I(R4).R4
Mas, se IG = 0 então I(R1)=I(R3) e I(R2)=I(R4)
Então:
VAC I ( R1 ).R1 VAD I ( R2 ).R2
=
=
=
VCB I ( R1 ).R3 VDB I ( R2 ).R4
R1 R2
=
R3 R4
Desta forma, se conhecermos R1, R2 e R3
poderemos determinar R4
A
2.1 – Ponte de Wheatstone
R1
) Determinar Rx se:
R1 = 2 kΩ
R2 = 4 kΩ
R3 = 6 kΩ
IG = 0
5V
C
R2
D
G
Rx
R3
B
Rx = 12 kΩ
) Determinar Rx se:
R1 = 2 kΩ
R2 = 4 kΩ
R3 = 6 kΩ
RG = 50Ω
IG = 50 µA (sentido C->D)
Rx = 9,617 kΩ
2.1A – Loop de Varley
x
Com S →1, Rx corresponde à resistência dos cabos (ida e volta) que estão
entre a subestação A e a subestação B.
Com S → 2, Rx corresponde à resistência dos cabos da ida A-B e da volta
até ao ponto x.
R3 real corresponde à soma de R3 com a resistência entre x e a
subestação A.
2.1A – Loop de Varley
x
Assim, Com S → 1 tem-se:
Com S → 2 tem-se
R1
R
= 2
R3 RTotal
R1
R2
=
R3 + RAX RTotal − RAX
Sabendo-se RAX e conhecendo-se as características do cabo (resistência por
unidade de comprimento) pode-se saber a que distância de A se encontra
o contacto ao solo.
2.2 – Ponte de Kelvin
- Utilizada para medir resistências de muito baixo valor.
- Permite ter em conta as resistências dos cabos e das soldaduras da própria ponte.
2.2 – Ponte de Kelvin
- Partindo da ponte de Wheatstone...
V
Se o valor da resistência Rx for muito baixo, então
Ra também o deve ser, para que a expressão:
Va
Vb
R1 R2
R
R
=
⇔ a = M
R3 R4
R X RN
se mantenha válida e a sensibilidade seja elevada
(valores de Va e Vb ~ V/2)
Assim, a corrente que flui no ramo esquerdo da ponte é de elevada intensidade!
→ As soldaduras e os fios ou (pistas impressas) da própria ponte provocam quedas
de potencial não desprezáveis:
Ewire, leads & contacts = Ewire = Rwire x I
2.2 – Ponte de Kelvin
Ewire, leads & contacts = Ewire = Rwire x I
Para que a ponte tenha em conta apenas a queda de potencial em Ra (ERa) e
em RX (ERx) teremos de poder descontar as quedas de tensão parasitas - Ewire.
2.2 – Ponte de Kelvin
Com esta modificação conseguimos
descontar o efeito dos topos da ponte
(Ewire),
Mas ainda se sentem os efeitos de
Ewire.
Por outro lado, os fios que unem a ponta inferior de Ra à ponta superior de Rx,
passando pelo galvanómetro, passam a ser percorridos por uma corrente forte e
teremos também aí mais Ewire!!!
2.2 – Ponte de Kelvin
Com esta nova modificação conseguimos
resolver o efeito da corrente pelo interior da
ponte, desde que as resistências utilizadas
sejam substancialmente maiores que as dos
fios/soldaduras.
Ainda existem os efeitos de
Ewire....mas...
Eles não são vistos pelo terminal esquerdo do galvanómetro desde que...
Se verifique a relação:
Rm RM
R
=
= a
Rn RN RX
2.2 – Ponte de Kelvin
Caso não se verifique esta proporcionalidade,
teremos sempre Rwire a influenciar a medida, uma
vez que, se IG = 0, se verifica a relação:
(1)
Quando
Rm RM
=
Rn RN
Então a expressão (1) simplifica-se para:
R X RN
=
Ra RM
Tornando-se análoga à ponte de Weatstone.
Apêndice X
Teorema de Thévenin (versão dc)
Qualquer circuito contendo apenas fontes de tensão, fontes de corrente e
resistências, pode ser convertido (simplificado) num circuito composto apenas
por uma fonte de tensão e uma resistência em série.
Apêndice X
Teorema de Thévenin (versão dc)
Regras para a obtenção de Vth e Rth:
1 – Vth: Determinar a tensão entre A e B em circuito aberto (sem nenhum
componente externo a unir os pontos A e B.
2 – Rth: Determinar a resistência equivalente entre os pontos A e B,
curtocircuitando todas as fontes.
Apêndice X
Teorema de Thévenin (versão dc)
) Determinar o circuito equivalente de Thévenin de uma ponte de
Wheatstone, do ponto de vista dos terminais do galvanómetro (retirando o
galvanómetro).
 R3
R4 

−
Vth = Va − Vb = V 
 R1 + R3 R2 + R4 
R1
V
a
R3
Rth = R1 // R3 + R2 // R4 =
R1 R3
RR
+ 2 4
R1 + R3 R2 + R4
R2
b
Rx
Apêndice X
 R3
R4 

−
Vth = Va − Vb = V 
+
+
R
R
R
R
3
2
4 
 1
Teorema de Thévenin (versão dc)
Rth = R1 // R3 + R2 // R4 =
R1 R3
RR
+ 2 4
R1 + R3 R2 + R4
) Resolver o problema anterior da ponte não equilibrada recorrendo ao
teorema de Thévenin.
Determinar Rx se:
R1 = 2 kΩ
R2 = 4 kΩ
R3 = 6 kΩ
IG = 50 µA (sentido A->B)
Rm = 50Ω
R1
V
R2
a
b
5V
R3
Rx
Circuitos de medida por anulação de corrente
3 – Pontes de Medida em ac
3 – Pontes de Medida em ac
Tal como nas pontes dc, também aqui
o detector ac indicará 0 se:
Va
Vb
Z1 Z 3
=
Z2 Z4
Note-se que para que o detector indique 0, terão de ocorrer
simultâneamente as condições:
- Vap = Vbp
- θ a = θ b.
i.e, não basta as ondas Va(t) e Vb(t) terem a mesma amplitude, elas devem coincidir no tempo.
3 – Pontes de Medida em ac
3.1 – Ponte simétrica
Trata-se de uma ponte de medida directa de impedâncias puras.
como R é o mesmo em ambos os ramos então a impedância desconhecida é igual à
impedância variável quando o detector ac indicar zero.
(Lx = Ls ou Cx = Cs)
3 – Pontes de Medida em ac
3.2 – Ponte de ângulo similar
Trata-se de uma ponte de medida de impedâncias compostas de natureza capacitiva.
Controlando R1 e R3 obtém-se o equilíbrio da ponte. Neste caso:
RX =
R2
R3
R1
CX =
R1
C3
R2
3 – Pontes de Medida em ac
3.3 – Ponte de Wien
Permite medir impedâncias compostas
de natureza capacitiva, quer estejam em
série ou em paralelo.
Em paralelo:
R3 =

R1 
1
 R4 + 2 2 2 
R2 
ω R4 C4 

R2 
C4


C3 =
2 2 2 

R1  1 + ω R4 C4 
Em série:
R1 
1
 C3 + 2 2
C4 =
R2 
ω R3 C3




R2 
R3


R4 =
2 2 2 

R1  1 + ω R3 C3 
3 – Pontes de Medida em ac
3.4 – Ponte de Maxwell
Permite medir impedâncias compostas de natureza indutiva, recorrendo a uma
impedância composta variável de natureza capacitiva.
Desta forma, no caso concreto teremos:
RX =
R2
R3
R1
LX = R2 R3C1
3 – Pontes de Medida em ac
Determinar o valor dos componentes Rx e Cx
da ponte de Wien ao lado:
a) Pela fórmula específica.
b) Pela fórmula geral.
a)
b)


1
 C3 + 2 2 
ω R3 C3 


R 
R3

R4 = 2 
2 2 2 
R1  1 + ω R3 C3 
C4 =
R1
R2
Z1 Z 2
=
Z3 Z4
(Rx)
(Cx)
Solução:
Rx= 898,5 Ω
Cx= 4,7 µF