Circuitos em ponte

Instrumentação e Técnicas de Medidas
Circuitos de Medida em Ponte
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
1
Controle de Versões
2013
Versão 1 – Com base nas notas de aula de COB783 e Op Amp Applications
Handbook, Section 4, edited by Walt Jung (Newnes, 2006).
Versção 1.1 – Ordem dos capítulos, equações mais comuns para linearização de
termistor.
Última alteração: 28/08/2013
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
2
Índice
10 Circuitos Condicionadores em Ponte de Wheatstone.....................................................................4
10.1.1 Medições de resistência em ponte de Wheatstone..........................................................8
10.1.2 Instrumentação para medidas remotas..........................................................................12
10.1.3 Problemas com offset....................................................................................................14
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
3
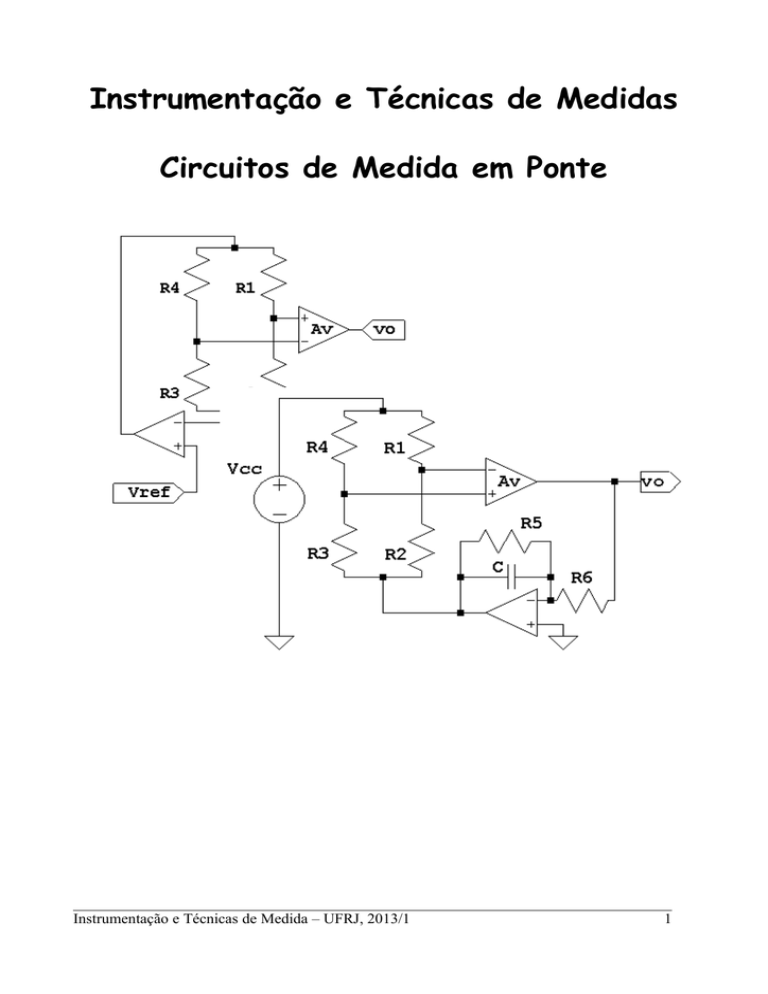
10 Circuitos Condicionadores em Ponte de Wheatstone
Vários transdutores como os RTDs e os strain gages apresentam pequenas variações de
resistência com relação a variável de interesse, e normalmente são utilizados em uma montagem
chamada ponte de Wheatstone (criada por S. H. Christie em 1883 e aprimorada por C Wheatstone
em 1843). Os sensores são colocados nos braços da ponte, que pode ser alimentada com fonte de
tensão ou corrente conforme indicado na figura abaixo. Na ponte, uma ou mais impedâncias mudam
seu valor proporcionalmente a grandeza que se deseja medir. Isto provoca um desequilíbrio nas
tensões da ponte que pode ser detectado por um amplificador. Eventualmente este amplificador
também pode ser responsável por linearizar ou filtrar o sinal captado da ponte.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
4
Apesar das duas formas serem possíveis a mais comum é aquela com alimentação em
tensão. Nela, considerando que Av é o ganho do amplificador e Vcc é o valor da fonte de
alimentação, a tensão na saída do amplificador será
(
v 0 = Av⋅Vcc⋅
)
R2
R3
−
,
R 1 +R2 R 3 +R4
enquanto que, para o circuito alimentado com fonte de corrente, o sinal na saída do
amplificador é dado por


R3 R4
R1 R 2
v O =Av⋅I⋅ R2⋅
−R3⋅
.
R 1R 2R 3R 4
R1 R2 R3 R 4
Em ambos os casos o amplificador foi considerado ideal, ou seja, com impedância de
entrada infinita. Isto nem sempre é verdade, e, assim como no caso apresentado para o circuito com
potenciômetro, se a impedância de entrada do amplificador não for infinita um erro sistemático será
adicionado a saída do circuito. A análise completa do problema, considerando a impedância de
entrada do amplificador, pode ser feita por meio de equivalentes Thévenin vistos a partir de cada
entrada do amplificador. Este foi o procedimento adotado abaixo para o caso da alimentação em
tensão mas pode ser facilmente estendido para o caso da alimentação em corrente.
Z3
v TH1=v⋅
Z 3Z 4
Z TH1 =
Z 3⋅Z 4
Z 3Z 4
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
5
v TH2 =v⋅
Z TH2 =
Z2
Z 1Z 2
Z 1⋅Z 2
Z 1Z 2




v TH =v TH1 −v TH2=v⋅
Z3
Z2
−
Z 3Z 4 Z 1Z 2
Z TH =Z TH1Z TH2 =
Z 3⋅Z 4
Z ⋅Z
 1 2
Z 3Z 4 Z 1 Z 2
Com as equações apresentadas fica evidente que a relação entre a tensão de saída da ponte e
a variação de resistência dos elementos sensores pode ser bastante complexa. Um caso de interesse
existe quando todos os elementos da ponte são resistivos e iguais e uma certa variação
(desbalanceamento) ocorre em apenas um dos braços, digamos o braço 4. Neste caso
Z 1=Z 2=Z 3=R e Z 4=R⋅1  .
Assim a tensão de Thévenin pode ser simplificada

R
R
−
RR⋅1  RR

1
1
−
2 2
v TH =v⋅
v TH =v⋅
v TH =v⋅


−
2⋅2 
assumindo pequenas variações de resistência, isto é,  pequeno (  ≪2 )

v TH =−v⋅ .
4
A resistência de Thévenin também pode ser recalculada como sendo
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
6
RTH =
R⋅R⋅1 
R⋅R

RR R R⋅1 
RTH =
R R⋅1 

2
2

RTH =R⋅
1 1

2 2

.
Assumindo  muito pequeno (muito menor do que 1)
RTH =R
Observe que tanto a tensão quanto a resistência de Thévenin variam em função das
variações de Z4, e que RTH é aproximadamente igual as resistências empregadas na ponte. Isto quer
dizer que o uso de sensores com impedância baixa é desejado, pois os erros relativos oriundos
destas variações e da impedância de entrada do amplificador serão baixos.
Outro caso de interesse ocorre quando existe um desbalanceamento igual e oposto em
braços laterais tal que Z 1=Z 2=R , Z 3= R⋅1−  e Z 4=R⋅1  .
Neste caso teremos
[
R⋅1− 
R
−
R⋅1− R⋅1  RR
[
1−  1
−
2
2
v TH =v⋅
v TH =v⋅
]
]

v TH =−v⋅ , e
2
RTH =
R⋅1− ⋅R⋅1 
R⋅R

RR R⋅1− R⋅1 
RTH =
R R⋅1− ⋅1 

.
2
2
Assumindo  muito pequeno (muito menor do que 1)
RTH =R
Neste caso, a tensão de saída da ponte é linear sem nenhuma aproximação nem restrição às
variações de resistência dos sensores. Apesar disto RTH ainda varia com a entrada. Várias outras
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
7
condições levam à VTH lineares seja com alimentação em tensão ou corrente. Convém notar,
entretanto, que resistências que variam da mesma forma devem ser colocadas em diagonal na ponte,
e resistências que variam de forma oposta devem ocupar posições em um mesmo braço.
As montagens de ponte mais comuns são aqueles onde apenas 1 elemento sensor está
presente na ponte (condição não linear), ou 2 elementos sensores estão presentes em um mesmo
braço da ponte (situação comum em medidores de pressão ou fluxo) ou todos os elementos da ponte
variam (este é quase um padrão industrial, sendo o tipo mais comum para células de carga). Para o
caso de dois elementos variando em um mesmo braço da ponte a saída não será linear se a ponte for
alimentada com tensão (terá a mesma não linearidade do caso com 1 sensor e o dobro da
sensibilidade).
A alimentação em corrente também apresenta um caso não linear, onde apenas uma
resistência da ponte varia. Mesmo nesta situação este tipo de alimentação pode ser vantajosa em
casos de alimentação remota, pois sofre menos influência da resistência dos fios e, portanto,
favorece o uso de cabos mais baratos e com menos fios (como será visto mais adiantes) além de ser
mais imune a interferências externas.
10.1.1 Medições de resistência em ponte de Wheatstone
Para entender o problema da medida de resistência pode se utilizar um exemplo numérico. O
RTD mais comum é o PT 100, um sensor de platina com resistência de 100Ω. Ele tem coeficiente
térmico (TC) aproximado de 0,385%/oC. Então para medir 1oC é necessário discriminar variações
de resistência de 0,385Ω. Outro exemplo são os strain gauges, eles podem variar 1% de seu valor
para o fundo de escala. Isto pode significar variação máxima de 3,5Ω numa medida de força. Para
medidas com resolução de 10 bits seria necessário detectar variações de resistência de
aproximadamente 0,0035Ω. Normalmente variações de resistência desta ordem de grandeza são
medidas com o uso de uma ponte de Wheatstone. A saída da ponte é de alguns mV quando a
alimentação é da ordem de 10V. Isto leva a sensibilidades de 1mV/V até 10mV/V.
Mesmo com a sensibilidade das pontes dependendo da tensão de alimentação esta não pode
ser aumentada indistintamente, pois leva a aquecimento dos sensores, e se este problema for
diminuído ao máximo, com a redução dos valores para fonte, a sensibilidade também fica muito
diminuída. Além disto fontes de alimentação para a ponte devem ser muito estáveis, pois variações
na tensão de alimentação produzem variação na sensibilidade da ponte. Para resolver este problema
pode se utilizar fontes de referência para alimentar as pontes. Existem fontes de referência muito
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
8
mais precisas do que as fontes de alimentação como por exemplo o AD589 (1,2%), o REF195
(0,2%) e o AD588 (0,01%) da Analog Devices. Uma alternativa para o uso de fontes de referência é
a medida na qual a tensão da fonte de alimentação é utilizada para corrigir o ganho do canal de
medição. Na figura abaixo a fonte de alimentação da ponte é usada como referência para o máximo
valor de conversão do ADC. Com este arranjo o conversor se adapta as variações da fonte
produzindo uma medida menos sensível as variações da fonte.
Com relação ao amplificador, normalmente utiliza-se o amplificador de instrumentação, seja
ele com dois ou três amplificadores operacionais. O amplificador de instrumentação apresenta
elevada impedância de entrada, elevado CMRR (anula a tensão de modo comum da ponte) e, de
preferência baixo ruído, offset e drift.
Apesar de todos estes cuidados o circuito acima continua sendo não linear, pois a ponte com
apenas um elemento variando (comum com RTD) não é linear. Neste caso
(
Vcc
Δ R/ R
v O =Av⋅ ⋅
4 1+Δ R/2R
)
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
9
o que significa que, para Vcc=10V, R=100Ω, ∆R=0,1% (0,1Ω) a tensão de saída da ponte
será Vo=2,49875mV. Isto nos leva a um erro de
Erro=
2,500000−2,49875
=0,05 % .
2,500000
Caso ∆R=1% (1,0Ω) a tensão de saída da ponte será Vo=24,8756mV. Isto nos leva a um
erro de
Erro=
25,00000−24,8756
=0,5 % .
25,00000
Assim sendo se percebe que a ponte apresenta uma linearidade de ∆R/2, independente do
sensor colocado nela ser ou não linear. O problema da linearidade deve, então, ser resolvido de
outra forma. Para linearizar esta ponte podem ser utilizados alguns circuitos com amplificadores
operacionais, tomando cuidado para que estes AOs sejam escolhidos em função do seu alto ganho,
baixo offset, baixo ruído e alta estabilidade térmica. Amplificadores como os AD708, OP2177,
OP213 e INA333 podem ser utilizados para esta função. Nas figuras abaixo todas as montagens
apresentam saída linear mesmo quando apenas um elemento da ponte varia.
V o=
( )
VB ΔR
R
⋅ ⋅ 1+ 1
2 R
R2
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
10
v 0=
Vcc
⋅Δ R
R
Se R6 =
Av⋅R 5
2
Vcc Δ R
⋅
4 R
então v O =Av⋅
Os circuitos a seguir também podem ser utilizados para linearizar pontes com um ou dois
elementos variando, conforme indicado, e alimentação em fonte de tensão. A desvantagem destes
circuitos é que as pontes precisam ser abertas, o que nem sempre é possível, pois algumas vezes a
ponte é comprada lacrada. A saída de cada uma das pontes será
( )
V o =−V B⋅
ΔR
2⋅R
para um elemento variando e
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
11
( )
V o =−V B⋅
ΔR
R
para dois elementos variando.
10.1.2 Instrumentação para medidas remotas
Para medidas remotas, onde a ponte é colada distante do circuito de excitação e captação, é
possível empregar técnicas que compensam os erros introduzidos pelos longos fios. Os métodos
mais conhecidos são os de extensões de três fios para a interconexão de um único elemento que
varia ou de seis fios para interconectar toda a ponte.
O esquema da figura abaixo ilustra o problema. Neste exemplo o elemento sensor esta
distante 30 metros do resto da ponte a qual ele está interconectado e a interconexão é feita por fios
AWG 30, de cobre, com um total de Rfio=10,5Ω @ 25oC e TC=0,385%/oC. A resistência dos fios
tira a ponte do equilíbrio, o que pode ser compensado com uma resistência Rcor=21Ω. Entretanto
variações de temperatura levam novamente a ponte ao desequilíbrio.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
12
Supondo VB=10V, R=350Ω, ∆R=1% para o fundo de escala, e Rfio=10,904Ω @ 35oC,
então a saída da ponte varia de acordo com as equações abaixo.
V o =0 – 23,45 mV @ 25 o C e
o
V o =5,44 – 28,83 mV @ 35 C .
Isto significa um erro de offset de +23% FS (5,44/23,45) e um erro de linearidade de -0,26%
FS ((28,83-5,44)/23,45). A correção para este problema pode ser feita não com o resistor de
correção (Rcor) mas com três fios que levam ao sensor (figura abaixo). Supondo as mesmas
condições do problema anterior, então a saída da ponte pode ser calculada como
V o =0 – 24,15 mV @ 25 o C e
V o =0 – 24,13 mV @ 35 o C .
Observa-se agora, um erro de offset nulo e um erro de sensibilidade de apenas 0,08% FS.
Isto ocorre pois a ponte ficou balanceada com a resistência dos fios que levam ao sensor e que
variam com a temperatura, mantendo a ponte permanentemente em equilíbrio.
Caso toda aponte esteja distante pode se adotar o uso de seis fios para interconectá-la. Neste
caso o maior problema é manter a alimentação da ponte o mais constante possível. A resistência dos
fios, entretanto, varia com a temperatura, o que se traduz em variações na tensão de alimentação da
ponte. O circuito apresentado na figura abaixo mostra como a alimentação sobre a ponte pode ser
mantida constante independente da impedância dos fios. Este sistema de medida com seis fios é,
algumas vezes, chamado de Kelvin. Apesar do efeito dos fios ter sido removido ainda é importante
manter a estabilidade da fonte de alimentação da ponte. A outra forma de evitar problemas com os
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
13
longos fios de interconexão é utilizar fonte de corrente para a alimentação da ponte. Em qualquer
um dos casos é importante atentar para a corrente de saída requerida para os amplificadores
operacionais. Com alimentação de 10V e resistências de 350Ω a corrente na saída dos operacionais
é da ordem de 30mA.
10.1.3 Problemas com offset
Outro problema que deve ser evitado é o do efeito termopar (diferença de tensão que surge
quando dois metais diferentes são unidos e mantidos em temperaturas diferentes) entre os fios que
conectam a ponte aos circuitos de captação de sinais. Para manter uma exatidão de 0,1%, ou
melhor, em uma ponte onde a saída máxima é de 20mV os erros devem ser menores do que 20µV
no offset.
O efeito de termopar entre fios de diferentes materiais como a solda e o cobre
(aproximadamente 2µV/oC) ou Kovar (material utilizado em alguns terminais de circuitos
integrados) e o cobre (aproximadamente 35µV/oC) ou entre cobre e terminais de borneiras,
conectores, chaves... Este problema só pode ser evitado mantendo as conexões que formam os
termopares na mesma temperatura, o que significa conexões próximas e sem barreiras entre elas.
Para minimizar problemas com offset e drift (causados por efeito termopar ou introduzidos
pelo próprio amplificador) a escolha do amplificador de instrumentação adequado pode ajudar. Os
operacionais OP177 e OP1177 apresentam baixo offset, drift, IB e ruído. Alternativamente podem
ser empregados integrados com arquitetura chopper estabilizadas como o ADA4528, o AD8629 ou
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
14
o AD8630, OPA335 e INA326. Também podem ser empregadas excitações alternadas com ondas
quadradas ou senoidais. A excitação com onda quadrada pode ser vista nas próximas figuras. Na
primeira a fonte EOS representa o offset do amplificador e não é afetado pela inversão da fonte. O
tratamento matemático pode ser feito com amostradores analógicos e subtratores ou digitalmente
após a conversão de um AD. A segunda figura mostra uma forma prática de inverter a polaridade na
tensão de alimentação da ponte. Esta inversão de polaridade pode ser feita por uma ponte H (um
DRV8832 por exemplo) ou por circuitos especialmente desenvolvidos para este condicionamento
como o AD7730.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
15
O AD7730 está preparado entre outras coisas para medidas com seis fios e apresenta
internamente circuitos digitais para compensação de offset e conversão AD. Seu uso não é simples e
requer programação feita por uma interface digital SPI.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
16
Outros integrados também podem ser utilizados para o condicionamento de sinais como o
PGA309 ou o XTR101 mostrados abaixo.
No caso do PGA309 a saída é feita em tensão, enquanto no XTR101 a saída se dá em
corrente (uma técnica muito utilizada na indústria). Os padrões mais comuns são de 4 a 20mA e de
0 a 20mA. No padrão de 4 até 20mA a corrente de offset serve para determinar se a linha de
transmissão está intacta ou partida e serve para alimentar o circuito. Alguns exemplos de circuitos
integrados que implementam estas funções são o XTR101 (4-20mA, 2 fios) e o XTR110 (0-20mA,
4-20mA, 5-25mA, 2 fios mais alimentação). Uma aplicação típica do XTR101 é mostrada na figura
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
17
abaixo. Os fios que levam alimentação para o integrado são os mesmos por onde circula a corrente
proporcional a variação de tensão sobre o elemento sensor.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
18