método dos esforços - IMS

ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
1 / 37
¾ MÉTODO DOS ESFORÇOS
Na resolução de estruturas hiperestáticas (aquelas que não podem ser resolvidas com as 3
equações fundamentais da estática , a saber : somatória forças verticais igual a zero , somatória
forças horizontais igual a zero , somatória momento fletor referente a um ponto igual a zero) , nós
podemos lançar mão do método dos esforços. Este processo de cálculo consiste na utilização de
uma estrutura equivalente a que desejamos calcular, na qual substituímos um vínculo entre barras
ou entre barra e apoio por um carregamento externo. Vejamos alguns exemplos de modificação
abaixo :
X
≡
≡
≡
X
X
X
X
X
≡
X
X
≡
≡
X
A estrutura equivalente deve ser isostática, caso a estrutura continue hiperestática após a
primeira modificação, executamos outra modificação e assim por diante até encontrar uma estrutura
equivalente isostática. A estrutura equivalente deve ser desdobrada em:
ISOSTÁTICA BÁSICA – corresponde a estrutura equivalente com os carregamentos externos da viga original .
CASO (1) – corresponde a estrutura equivalente com o carregamento originado pela primeira modificação.
CASO (2) – corresponde a estrutura equivalente com o carregamento originado pela segunda modificação.
CASO (n) – corresponde a estrutura equivalente com o carregamento originado pela enésima modificação.
Vale um comentário quanto a numeração da estrutura: deve-se procurar numerar os nós da
estrutura de forma que o ponto 1 coincida com a modificação 1 , o ponto 2 com a modificação 2 e
assim por diante, e, caso seja possível, desaconselha-se duas modificações no mesmo nó.
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
2 / 37
Para conseguirmos determinar as incógnitas que superam o número de equações
fundamentais da Estática vamos usar equações de compatibilidade de deformação (seja esta
deformação a flecha, o giro, ou o giro relativo). Ou seja , valendo a sobreposição de efeitos :
-
na modificação do apoio móvel do nó “1” por uma força “X”, temos que a soma da flecha
devida ao carregamento externo original com a flecha devida a força “X” será igual a zero
(condição de apoio na estrutura original).
δ1R = δ10 + δ11 → 0 = δ10 + δ11
-
na modificação do engastamento do nó “1” por um momento fletor “X” e um apoio fixo, temos
que a soma do giro devido ao carregamento externo original com o giro devido ao momento
“X” será igual a zero (condição de engastamento na estrutura original).
ϕ1R = ϕ10 + ϕ11 → 0 = ϕ10 + ϕ11
-
na modificação da ligação rígida entre barras no nó “1” por uma articulação com momentos
fletores relativos “X”, diremos que a soma do giro relativo devido ao carregamento externo
original com o giro relativo devido aos momentos fletores relativos “X” será igual a zero
(condição de ligação rígida - continuidade - na estrutura original).
ϕR1R = ϕR10 + ϕR11 → 0 = ϕR10 + ϕR11
Os cálculos relativos a flecha, giro e giro relativo serão desenvolvidos com o Teorema de
Castigliano e auxílio da Tabela de Kurt Beyer. Para tanto devemos construir os diagramas de
momento fletor da Isostática Básica e dos “n” Casos. Uma vez que o Teorema de Castigliano utiliza
de um diagrama de momento gerado por um carregamento unitário, convém em cada Caso (“n”)
colocarmos em evidência Xn tornando assim cada Caso (“n”) em um carregamento unitário
multiplicado por Xn.
Cria-se a equação de compatibilidade na seguinte forma :
REAL = CASO (0) + X1 . CASO (1) + X2 . CASO (2) + ... + Xn . CASO (n)
Castigliano :
δ =∫
M o ⋅ M1
M ⋅ M1
M ⋅ M1
⋅ dx , ϕ = ∫ o
⋅ dx , ϕ R = ∫ o
⋅ dx
E⋅I
E⋅I
E⋅I
Encontradas as deformações por Castigliano , montamos um sistema linear devido as
equações de compatibilidade com a seguinte forma :
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
⎧ϕ 1R = ϕ 10 + X 1 .ϕ 11 + X 2 .ϕ 12 + ... + X n .ϕ 1n
⎪ϕ = ϕ + X .ϕ + X .ϕ + ... + X .ϕ
⎪ 2R
20
1
21
2
22
n
2n
⎨
....
.....
....
.....
⎪ ...
⎪⎩ϕ nR = ϕ n 0 + X 1 .ϕ n1 + X 2 .ϕ n 2 + ... + X n .ϕ nn
3 / 37
⎧0 = ϕ 10 + X 1 .ϕ 11 + X 2 .ϕ 12 + ... + X n .ϕ 1n
⎪0 = ϕ + X .ϕ + X .ϕ + ... + X .ϕ
⎪
20
1
21
2
22
n
2n
⎨
....
.....
....
.....
⎪ ...
⎪⎩0 = ϕ n 0 + X 1 .ϕ n1 + X 2 .ϕ n 2 + ... + X n .ϕ nn
Os valores encontrados nos fornecem os vínculos ou esforços internos aos quais se referem,
tornando possível agora a resolução da estrutura original utilizando-se as 3 equações fundamentais
da estática, seguindo o cálculo das reações de apoio e a construção dos diagramas de esforços
internos solicitantes da estrutura original, a saber N (esforço normal) , V (esforço cortante) e M
(momento fletor) .
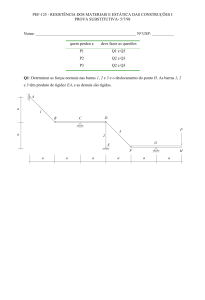
EXERCÍCIO 01 : Na viga contínua esquematizada abaixo , calcular os diagramas de
esforços internos solicitantes :
1,5 m
2,0 m
40 kN
30 kN
20 kN/m
3,0 m
4,0 m
E , I → constantes
Resolução :
ƒ
Definição da viga equivalente e numeração da estrutura (Caso Real) :
1,5 m
2,0 m
40 kN
30 kN
ϕR1R = 0
X
0
20 kN/m
X
2
1
3,0 m
4,0 m
ESTÁTICA DAS ESTRUTURAS I
ƒ
PROF. IBERÊ
4 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
1,5 m
2,0 m
40 kN
30 kN
ϕR10
20 kN/m
CASO (0)
0
2
1
3,0 m
4,0 m
M0
kN.m
22,5
40,0
+
kN.m
M0
30,0
30,0
ϕR11
X . CASO (1)
1,0
1,0
0
2
1
3,0 m
4,0 m
M1
kN.m
1,0
ƒ
Cálculo dos giros relativos ϕR10 , ϕR11 por Castigliano :
ϕ R10 = ∫
ϕ R10 =
M 0 .M 1
.dx
E .I
1
1 ⎛ s.i.k s.i.k s.i.k
s.i.k
⎞
+
+
.∫ M 0 .M 1 .dx =
.⎜
.(1 + α ) +
.(1 + β )⎟
3
6
6
E.I
E.I ⎝ 3
⎠
ESTÁTICA DAS ESTRUTURAS I
ϕ R10 =
ƒ
5 / 37
385
1 ⎛ 3.22,5.1 4.40.1 3.30.1
4.30.1
⎞
+
+
.⎜
.(1 + 0,5) +
.(1 + 0,5)⎟ = +
E .I ⎝ 3
3
6
6
3.E.I
⎠
ϕ R11 = ∫
ϕ R10 =
PROF. IBERÊ
M 1 .M 1
.dx
E.I
1
1 ⎛ s.i.k s.i.k ⎞
1 ⎛ 3.1.1 4.1.1 ⎞
7
.∫ M 1 .M 1 .dx =
.⎜
.⎜
+
+
⎟=
⎟=+
E.I
E.I ⎝ 3
3 ⎠ E.I ⎝ 3
3 ⎠
3.E.I
Montagem sistema linear com equação de compatibilidade :
(R)=(0)+X.(1)
0=+
385
7
+ X.
3.E.I
3.E.I
⇒
⇒
ϕR1R = ϕR10 + X . ϕR11
X =−
385 3.E.I
.
= −55,00
3.E.I 7
∴ podemos assim afirmar que o momento fletor no apoio (1) assume o valor X . 1,0 kN.m , ou seja,
vale –55,00 kN.m . O sinal negativo indica que ele assume sentido contrário ao escolhido na
proposição do caso (1) .
ƒ
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
∑ M esq1 = −55,00 ⇒ − 55 = + RV 0 .3 − 40.1,5 − 20.3.1,5 ⇒
∑ M dir1 = −55,00 ⇒ − 55 = + RV 2 .4 − 30.2 − 20.4.2 ⇒ R
∑ FV = 0 ⇒ + RV 0 + RV 1 + RV 2 − 40 − 30 − 7.20 = 0 ⇒ R
∑ FH = 0 ⇒ RH 2 = 0
RV 0 = +31, 67kN
V2
= +41, 25kN
V1
= +137, 08kN
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
6 / 37
1,5 m
2,0 m
40 kN
30 kN
20 kN/m
RH 2
0
RV 0
2
1
RV 1
3,0 m
RV 2
4,0 m
+
–
N
0
[kN]
68,75
31,67
+
–
V
38,33
28,75
+
1,67
+
1,25
–
–
[kN]
41,25
68,33
55,00
–
M+
[kN.m]
25,00
42,50
EXERCÍCIO 02 : Na viga contínua esquematizada abaixo , calcular os diagramas de
esforços internos solicitantes :
2,0 m
30 kN
20
40 kN/m
kN
/m
I
3,0 m
E → constante
3.I
3,0 m
3.I
1,0 m
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
7 / 37
Resolução :
ƒ
Definição da viga equivalente e numeração da estrutura (Caso Real) :
2,0 m
40 kN
ϕR1R = 0
30 kN
20
40
kN
/m
kN
/m
20 kN.m
I
0
X
1
3.I
X
2
3,0 m
ƒ
3,0 m
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
2,0 m
40 kN
30 kN
ϕR10
40 kN/m
20 kN/m
20 kN.m
CASO (0)
I
3.I
0
1
3,0 m
2
3,0 m
M0
kN.m
22,5
+
45,0
20,0
kN.m
M0
20,0
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
8 / 37
ϕR11
X . CASO (1)
1,0
1,0
0
2
1
3,0 m
3,0 m
M1
kN.m
1,0
ƒ
Cálculo dos giros relativos ϕR10 , ϕR11 por Castigliano :
ϕ R10
2
1
M 0 .M 1
M 0 .M 1
M 0 .M 1
1 1
1 2
.dx = ∫
.dx + ∫
.dx =
.∫ M 0 .M 1 .dx +
=∫
.∫ M 0 .M 1 .dx
E
.
I
3
.
E
.
I
E
I
E
I
E.I
.
3
.
.
1
0
0
1
ϕ R10 =
1 ⎛ s.i.k s.i.k
1 ⎛ s.i.k s.i.k ⎞
⎞
.⎜
.(1 + α )⎟ +
.⎜
+
−
⎟
6
6 ⎠
E.I ⎝ 3
⎠ 3.E.I ⎝ 3
ϕ R10 =
305
1 ⎛ 3.22,5.1 3.1.20 ⎛ 2 ⎞ ⎞
1 ⎛ 3.45.1 3.1.20 ⎞
.⎜
.⎜1 + ⎟ ⎟ +
.⎜
+
−
⎟=+
E.I ⎝ 3
6 ⎝ 3 ⎠ ⎠ 3.E.I ⎝ 3
6 ⎠
6.E.I
ϕ R11
1
2
M 1 .M 1
M 1 .M 1
M 1 .M 1
1 1
1 2
.dx = ∫
.dx + ∫
.dx =
. M 1 .M 1 .dx +
=∫
. M 1 .M 1 .dx
E.I
E.I
E.I ∫0
3.E.I
3.E.I ∫1
0
1
ϕ R10 =
ƒ
1 ⎛ s.i.k ⎞
1 ⎛ s.i.k ⎞
1 ⎛ 3.1.1 ⎞
1 ⎛ 3.1.1 ⎞
4
.⎜
.⎜
.⎜
.⎜
⎟+
⎟=
⎟+
⎟=+
E.I ⎝ 3 ⎠ 3.E.I ⎝ 3 ⎠ E.I ⎝ 3 ⎠ 3.E.I ⎝ 3 ⎠
3.E.I
Montagem sistema linear com equação de compatibilidade :
(R)=(0)+X.(1)
0=+
305
4
+ X.
6.E.I
3.E.I
⇒
⇒
ϕR1R = ϕR10 + X . ϕR11
X =−
305 3.E.I
.
= −38,12
6.E.I 4
∴ podemos assim afirmar que o momento fletor no apoio (1) assume o valor X . 1,0 kN.m , ou seja,
vale –38,12 kN.m . O sinal negativo indica que ele assume sentido contrário ao escolhido na
proposição do caso (1) .
ƒ
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
9 / 37
∑ M esq1 = −38,12 ⇒ − 38,12 = + RV 0 .3 − 30.1 − 20.3.1,5 ⇒ R = +27, 29kN
∑ M dir1 = −38,12 ⇒ − 38,12 = + RV 2 .3 − 40.4.2 ⇒ R = +93,96kN
∑ FV = 0 ⇒ + RV 0 + RV 1 + RV 2 − 30 − 3.20 − 4.40 = 0 ⇒ R = +128, 75kN
∑ FH = 0 ⇒ RH 0 = 0
V0
V2
V1
2,0 m
30 kN
20
40 kN/m
kN
/m
RH 0
I
0
RV 0
N
3.I
1
RV 1
3,0 m
3,0 m
3.I
2
RV 2
1,0 m
+
–
0
[kN]
66,04
40,00
27,29
V
+
–
+
+
12,71
+
[kN]
–
–
42,71
53,96
62,71
1,35
1,365
38,12
20,00
–
M+
[kN.m]
18,62
16,42
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
10 / 37
EXERCÍCIO 03 : Na viga contínua esquematizada abaixo , calcular os diagramas de
esforços internos solicitantes :
24 kN/m
18 kN/m
4,0 m
3,0 m
3,0 m
1,0 m
E , I → constantes
Resolução :
ƒ
Definição da viga equivalente e numeração da estrutura (Caso Real) :
ϕR2R = 0
24 kN/m
ϕR3R = 0
18
ϕ1R = 0
18 kN
kN
/m
9 kN.m
X1
X2
1
2
4,0 m
ƒ
X3
X2
3
X3
4
3,0 m
3,0 m
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
ϕR20
24 kN/m
ϕR30
18 kN
18 kN/m
CASO (0)
ϕ10
9 kN.m
1
3
2
4,0 m
3,0 m
4
3,0 m
M0
kN.m
48,00
20,25
+
M0
20,25
9,00
kN.m
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
ϕ11
11 / 37
ϕR31
ϕR21
X1 . CASO (1)
1,00
1
3
2
4,0 m
4
3,0 m
3,0 m
M1
kN.m
1,00
ϕ12
ϕR32
ϕR22
X2 . CASO (2)
1,00
1
2
4,0 m
1,00
3
4
3,0 m
3,0 m
M2
kN.m
1,00
ϕ13
ϕR23
1
2
ϕR33
X3 . CASO (3)
4,0 m
1,00
3
1,00
4
3,0 m
3,0 m
M3
kN.m
1,00
ƒ
Cálculo dos giros relativos ϕR20 , ϕR30 , ϕR21 , ϕR22 , ϕR23 , ϕR31 , ϕR32 , ϕR33 , e dos giros ϕ10 , ϕ11 , ϕ12 ,
ϕ13,
por Castigliano :
ϕ10 = ∫
M 0 .M 1
1
1 ⎛ s.i.k ⎞
1 ⎛ 4.48.1 ⎞
64
.dx =
.∫ M 0 .M 1.dx =
.⎜
.⎜
⎟=+
⎟=
E .I
E.I
E .I ⎝ 3 ⎠ E .I ⎝ 3 ⎠
E.I
ϕ11 = ∫
M 1.M 1
1
1 ⎛ s.i.k ⎞
1 ⎛ 4.1.1 ⎞
4
.⎜
.⎜
.dx =
.∫ M 1.M 1.dx =
⎟=+
⎟=
E .I
E .I
E.I ⎝ 3 ⎠ E.I ⎝ 3 ⎠
3.E.I
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
12 / 37
ϕ12 = ϕ R 21 = ∫
M 1.M 2
1
1 ⎛ s.i.k ⎞
1 ⎛ 4.1.1 ⎞
2
.dx =
.∫ M 1.M 2 .dx =
.⎜
.⎜
⎟=+
⎟=
E .I
E .I
E .I ⎝ 6 ⎠ E .I ⎝ 6 ⎠
3.E.I
ϕ13 = ϕ R 31 = ∫
M 1.M 3
1
1
.dx =
.∫ M 1.M 3 .dx =
.0 = 0
E .I
E .I
E .I
ϕ R 20 = ∫
M 0 .M 2
1
1 ⎛ s.i.k s.i.k ⎞
1 ⎛ 4.48.1 3.20,25.1 ⎞
.dx =
.∫ M 0 .M 2 .dx =
.⎜
.⎜
+
+
⎟
⎟=
E .I
E .I
E .I ⎝ 3
3 ⎠ E .I ⎝ 3
3
⎠
ϕ R 20 = +
337
4.E.I
ϕ R 22 = ∫
M 2 .M 2
1
1 ⎛ s.i.k s.i.k ⎞
1 ⎛ 4.1.1 3.1.1 ⎞
7
.dx =
.∫ M 2 .M 2 .dx =
.⎜
.⎜
+
+
⎟=+
⎟=
E.I
E.I
E.I ⎝ 3
3 ⎠ E .I ⎝ 3
3 ⎠
3.E.I
ϕ R 23 = ϕ R 32 = ∫
ϕ R 30 = ∫
ϕ R 30 =
M 0 .M 3
1
1 ⎛ s.i.k s.i.k s.i.k ⎞
.dx =
.∫ M 0 .M 3 .dx =
.⎜
+
−
⎟
E .I
E .I
E .I ⎝ 3
3
6 ⎠
1 ⎛ 3.20,25.1 3.20,25.1 3.9.1 ⎞ 36
.⎜
+
−
⎟=
E .I ⎝
3
3
6 ⎠ E.I
ϕ R33 = ∫
ƒ
M 2 .M 3
1
1 ⎛ s.i.k ⎞
1 ⎛ 3.1.1 ⎞
1
.dx =
.∫ M 2 .M 3 .dx =
.⎜
.⎜
⎟=+
⎟=
E .I
E.I
E.I ⎝ 6 ⎠ E.I ⎝ 6 ⎠
2.E.I
M 3 .M 3
1
1 ⎛ s.i.k s.i.k ⎞
1 ⎛ 3.1.1 3.1.1 ⎞
2
.⎜
.⎜
.dx =
.∫ M 3 .M 3 .dx =
+
+
⎟=+
⎟=
E.I
E.I
E.I ⎝ 3
3 ⎠ E.I ⎝ 3
3 ⎠
E.I
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) + X2 . ( 2 ) + X3 . ( 3 )
⇒
⎧0 = ϕ10 + X 1.ϕ11 + X 2 .ϕ12 + X 3 .ϕ13
⎪
⎨0 = ϕ R 20 + X 1 .ϕ R 21 + X 2 .ϕ R 22 + X 3 .ϕ R 23
⎪0 = ϕ
R 30 + X 1 .ϕ R 31 + X 2 .ϕ R 32 + X 3 .ϕ R 33
⎩
resolvendo o sistema por forma matricial :
ϕ12
ϕ13 ⎤ ⎡ X 1 ⎤ ⎡ − ϕ10 ⎤
⎡ ϕ11
⎢ϕ
⎥ ⎢ ⎥ ⎢
⎥
⎢ R 21 ϕ R 22 ϕ R 23 ⎥ ⋅ ⎢ X 2 ⎥ = ⎢− ϕ R 20 ⎥
⎢⎣ϕ R 31 ϕ R 32 ϕ R 33 ⎥⎦ ⎢⎣ X 3 ⎥⎦ ⎢⎣ − ϕ R30 ⎥⎦
⇒
0 ⎤ ⎡ X 1 ⎤ ⎡− 64,00⎤
⎡ 1,33 0,67
⎢0,67 2,33 0,50 ⎥ ⋅ ⎢ X ⎥ = ⎢ − 84,25⎥
⎢
⎥ ⎢ 2⎥ ⎢
⎥
⎢⎣ 0
0,50 2,00⎥⎦ ⎢⎣ X 3 ⎥⎦ ⎢⎣ − 36,00⎥⎦
X 1 = −36,47
∴ X 2 = −23,07
X 3 = −12,23
∴ podemos assim afirmar que : o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale –36,47 kN.m ; o momento fletor no apoio (2) assume o valor X2 . 1,0 kN.m , ou seja,
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
13 / 37
vale –23,07 kN.m ; o momento fletor no apoio (3) assume o valor X3 . 1,0 kN.m , ou seja, vale –12,23
kN.m . O sinal negativo indica que os momentos assumem sentido contrário ao escolhido na
proposição dos casos .
ƒ
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
∑ M esq 2 = −23,07
⇒
− 23,07 = −36,47 + RV 1 .4 − 24.4.2
∑ M esq3 = −12,23
⇒
− 12,23 = −36,47 + 51,35.7 − 24.4.2 + RV 2 .3 − 18.3.1,5
∑ M dir 3 = −12,23
⇒
− 12,23 = −18.4.2 + RV 4 .3
∑ M dir 2 = −23,07
⇒
− 23,07 = −18.7.3,5 + 43,92.6 + RV 3 .3
∑ FH
⇒
=0
RH1 = 0
⇒
RV 1 = +51,35kN
⇒ RV 2 = +75, 26kN
⇒ RV 4 = +43,92kN
⇒ RV 3 = +51, 47kN
RH 4 = 0
;
24 kN/m
18 kN/m
RH 4
RH 1
4,0 m
N
RV 3
RV 2
RV 1
RV 4
3,0 m
3,0 m
1,0 m
+
–
0
[kN]
51,35
30,61
V
+
–
+
28,08
+
18,00
+
+
–
–
2,14 m
23,39
25,92
44,65
36,47
1,70 m
[kN]
–
1,56 m
23,07
12,23
M
–
+
9,00
[kN.m]
2,95
9,67
18,48
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
14 / 37
EXERCÍCIO 04 : Na viga hiperestática esquematizada abaixo , calcular os diagramas
de esforços internos solicitantes :
20 kN/m
4,0 m
E , I → constantes
Resolução :
a) utilizando a flecha do apoio (1) para montagem da equação de compatibilidade :
ƒ
Definição da viga equivalente e numeração da estrutura (Caso Real) :
20 kN/m
δ1R = 0
0
1
X
4,0 m
ƒ
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
20 kN/m
160
CASO (0)
0
δ10
M0
kN.m
δ11
M1
kN.m
1
4,0 m
X . CASO (1)
1
0
1,0 kN
4,0 m
ƒ
4
Cálculo das flechas δ10 , δ11 por Castigliano :
δ 10 = ∫
M 0 .M 1
1
1 ⎛ s.i.k ⎞ 1 ⎛ 4.160.4 ⎞
640
.dx =
.∫ M 0 .M 1 .dx =
.⎜ −
.⎜ −
⎟=
⎟=−
4 ⎠ E .I ⎝
E.I
E .I
E.I ⎝
4 ⎠
E.I
ESTÁTICA DAS ESTRUTURAS I
δ 11 = ∫
ƒ
PROF. IBERÊ
15 / 37
M 1 .M 1
1
1 ⎛ s.i.k ⎞
1 ⎛ 4.4.4 ⎞
64
.dx =
.∫ M 1 .M 1 .dx =
.⎜
.⎜
⎟=
⎟=
E .I
E.I
E.I ⎝ 3 ⎠ E.I ⎝ 3 ⎠ 3.E.I
Montagem sistema linear com equação de compatibilidade :
⇒
(R)=(0)+X.(1)
0=−
64
640
+ X.
E.I
3.E.I
⇒
δ1R = δ10 + X . δ11
X =+
640 3.E.I
.
= 30,00
E.I 64
∴ podemos assim afirmar que a reação vertical no apoio (1) assume o valor X . 1,0 kN , ou seja,
vale 30,00 kN . O sinal positivo indica que ela assume o mesmo sentido escolhido na proposição do
caso (1).
ƒ
Cálculo das Reações de Apoio
∑M0 = 0
⇒
− M R 0 − 30.4 + 20.4.2 = 0
∑ FV
=0
⇒
+ RV 0 + 30 − 4.20 = 0
∑ FH
=0
⇒
RH 0 = 0
⇒
⇒
M R 0 = +40, 00kN
RV 0 = +50, 00kN
b) utilizando o giro do engaste (1) para montagem da equação de compatibilidade :
ƒ
Definição da viga equivalente e numeração da estrutura (Caso Real) :
20 kN/m
X
ϕ1R = 0
1
2
4,0
ƒ
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
20 kN/m
CASO
kN.m
M0
ϕ10
1
2
4,0
40
1
1,0 kN.m
X . CASO (1)
M1
ϕ11
1
2
4,0
kN.m
ESTÁTICA DAS ESTRUTURAS I
ƒ
PROF. IBERÊ
16 / 37
Cálculo dos giros ϕ10 , ϕ11 por Castigliano :
ϕ 10 = ∫
M 0 .M 1
1
1 ⎛ s.i.k ⎞
1 ⎛ 4.40.1 ⎞
160
.dx =
.∫ M 0 .M 1 .dx =
.⎜ −
.⎜ −
⎟=
⎟=−
E .I
E .I
E .I ⎝ 3 ⎠ E .I ⎝
3 ⎠
3.E.I
ϕ 11 = ∫
M 1 .M 1
1
1 ⎛ s.i.k ⎞ 1 ⎛ 4.1.1 ⎞
4
.dx =
.∫ M 1 .M 1 .dx =
.⎜
.⎜
⎟=
⎟=
E .I
E.I
E.I ⎝ 3 ⎠ E.I ⎝ 3 ⎠ 3.E.I
ƒ
Montagem sistema linear com equação de compatibilidade :
⇒
(R)=(0)+X.(1)
0=−
160
4
+ X.
3.E.I
3.E.I
⇒
ϕ1R = ϕ10 + X . ϕ11
X =+
160 3.E.I
.
= 40,00
3.E.I 4
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X . 1,0 kN.m , ou
seja, vale 40,00 kN.m . O sinal positivo indica que ela assume o mesmo sentido escolhido na
proposição do caso (1) .
ƒ
Cálculo das Reações de Apoio
∑M0 = 0
⇒
− 40 − RV 1 .4 + 20.4.2 = 0
∑ FV
=0
⇒
+ RV 0 + 30 − 4.20 = 0
∑ FH
=0
⇒
RH 0 = 0
⇒
⇒
RV 1 = +30, 00kN
RV 0 = +50, 00kN
20 kN/m
Diagramas de Esforços Internos Solicitantes
MR0
RH 0
0
RV 1
RV 0
4,0
N
+
–
0
[kN]
50,0
V
+
–
Nota : O exercício foi resolvido de duas
+
[kN]
–
2,50 m
30,0
40,00
maneiras possíveis para demonstrar o método ,
no caso poderia ser utilizada a resolução a) ou
b) , que resultaram iguais como podemos
comprovar no item de cálculo das reações.
M +–
22,50
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
17 / 37
EXERCÍCIO 05 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
32 kN/m
2,0 m
3,0 m
24 kN
E , I → constantes
6,0 m
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
32 kN/m
24 kN
3
3,0 m
4
2
2,0 m
ƒ
ϕ1R = 0
E , I → constantes
1
X1
6,0 m
ESTÁTICA DAS ESTRUTURAS I
18 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
32 kN/m
CASO (0)
24 kN
3
4
∑F
H
=0
3,0 m
+ 24 − RH 1 = 0
R H 1 = 24
∑M
2
1
=0
+ RV 2 .6 + 24.5 − 32.6.3 = 0
RV 2 = 76
2,0 m
ƒ
PROF. IBERÊ
76 kN
1
∑F
ϕ10
V
=0
RV 1 + 76 − 32.6 = 0
24 kN
RV 1 = 116
116 kN
6,0 m
3
3
0
4
4
144,00
120,00
2
3
4
M0
[ kN.m ]
1
120,00
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
3
19 / 37
X1 . CASO (1)
4
3,0 m
∑F
H
RH 1 = 0
∑M
2
1
=0
2,0 m
+ RV 2 .6 − 1 = 0
RV 2 =
1
/6 kN
1
∑F
ϕ11
V
1,00
RV 1 =
1
/6 kN
6,0 m
3
3
4
1,00
4
1,00
1
1,00
0
2
M1
[ kN.m ]
Cálculo dos giros ϕ10 , ϕ11 , por Castigliano :
ϕ 10 = ∫
ϕ10 =
ϕ11 = ∫
ϕ11 =
M 0 .M 1
1
1 ⎛ s.i.k s.i.k s.i.k ⎞
.∫ M 0 .M 1 .dx =
.⎜
.dx =
−
−
⎟
E.I
E.I
E.I ⎝ 3
3
2 ⎠
1 ⎛ 6.1.144 6.1.120 5.1.120 ⎞
252
.⎜
−
−
⎟=−
E .I ⎝ 3
3
2 ⎠
E .I
M 1 .M 1
1
1 ⎛ s.i.k
⎞
.dx =
.∫ M 1 .M 1 .dx =
.⎜
+ s.i.k ⎟
E .I
E.I
E.I ⎝ 3
⎠
7
1 ⎛ 6.1.1
⎞
.⎜
+ 5.1.1⎟ = +
E.I ⎝ 3
E .I
⎠
1
6
=0
− RV 1 + 1 6 = 0
0
ƒ
=0
1
6
ESTÁTICA DAS ESTRUTURAS I
ƒ
PROF. IBERÊ
20 / 37
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) ⇒
0 = ϕ 10 + X 1 .ϕ 11
⇒
X1 = −
ϕ 10
ϕ 11
⎛ 252 ⎞ E.I
X 1 = −⎜ −
= 36,00
⎟⋅
⎝ E.I ⎠ 7
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale 36,00 kN.m . O sinal positivo indica que o momento assume o mesmo sentido ao
escolhido na proposição dos casos .
ƒ
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
RV 1 = 116, 00 + 36, 00. ( − 1 6 ) = 110, 00 kN
RH 1 = 24, 00 + 36, 00. ( 0 ) = 24, 00 kN
RV 2 = 76, 00 + 36, 00. ( + 1 6 ) = 82, 00 kN
0
82,00
110,00
–
–
82,00
N
[ kN ]
110,00
82,00
+
24,00
–
0
110,00
+
2,56 m
V
[ kN ]
24,00
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
21 / 37
84,00
84,00
0
105,06
2,56 m
M
[ kN.m ]
36,00
EXERCÍCIO 06 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
36 kN/m
2,0 m
2,0 m
18 kN
E , I → constantes
4,0 m
Resolução :
ƒ
Definição da estrutura equivalente e numeração (Caso Real) :
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
22 / 37
36 kN/m
18 kN
4
2,0 m
3
2,0 m
2
ϕ1R = 0
1
X1
4,0 m
Desmembramento da estrutura em Caso (0) – Isostática Básica e Caso (1) , com seus respectivos
gráficos de momento fletor :
36 kN/m
CASO (0)
18 kN
4
∑F
3
2,0 m
H
=0
− 18 + R H 1 = 0
RH 1 = 18
∑M
2
1
=0
− RV 2 .4 − 18.4 + 36.4.2 = 0
54 kN
2,0 m
ƒ
E , I → constantes
RV 2 = 54
∑F
V
18 kN
1
ϕ10
=0
RV 1 + 54 − 36.4 = 0
RV 1 = 90
90 kN
4,0 m
ESTÁTICA DAS ESTRUTURAS I
72,00
PROF. IBERÊ
23 / 37
3
4
4
3
0
72,00
72,00
2
3
4
M0
1
4
[ kN.m ]
X1 . CASO (1)
2,0 m
3
∑F
H
=0
RH 1 = 0
∑M
2
/4 kN
0
1,00
1
=0
+ RV 2 .4 − 1 = 0
2,0 m
1
1
RV 2 =
∑F
ϕ11
1
4
=0
V
RV 1 − 1 4 = 0
RV 1 =
1
/4 kN
4,0 m
1,00
3
1,00
4
3
4
0
2
1,00
1,00
M1
1
[ kN.m ]
1
4
ESTÁTICA DAS ESTRUTURAS I
ƒ
24 / 37
Cálculo dos giros ϕ10 , ϕ11 , por Castigliano :
ϕ 10 = ∫
ϕ 10 =
ϕ 11 =
M 0 .M 1
1
1 ⎛ s.i.k s.i.k s.i.k ⎞
.dx =
.∫ M 0 .M 1 .dx =
.⎜
−
−
⎟
E.I
E.I
E.I ⎝ 3
3
2 ⎠
1 ⎛ 4.1.72 4.1.72 4.1.72 ⎞
144
.⎜ −
+
+
⎟=+
E.I ⎝
3
3
2 ⎠
E .I
ϕ11 = ∫
ƒ
PROF. IBERÊ
M 1 .M 1
1
1 ⎛ s.i.k
⎞
.dx =
.∫ M 1 .M 1 .dx =
.⎜
+ s.i.k ⎟
E .I
E.I
E.I ⎝ 3
⎠
1 ⎛ 4.1.1
16
⎞
.⎜
+ 4.1.1⎟ = +
E.I ⎝ 3
3.E.I
⎠
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) ⇒
X1 = −
0 = ϕ 10 + X 1 .ϕ 11
⇒
X1 = −
ϕ 10
ϕ 11
144 3.E.I
⋅
= −27,00
E.I 16
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale 27,00 kN.m . O sinal negativo indica que o momento assume o sentido contrário ao
escolhido na proposição dos casos .
ƒ
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
RV 1 = 90, 00 − 27, 00. ( + 1 4 ) = 83, 25 kN
RH 1 = 18, 00 − 27, 00. ( 0 ) = 18, 00 kN
RV 2 = 54, 00 − 27, 00. ( − 1 4 ) = 60, 75 kN
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
25 / 37
0
83,25
60,75
–
–
60,75
N
83,25
[ kN ]
83,25
+
18,00
–
60,75
0
–
1,69 m
V
18,00
[ kN ]
45,00
45,00
0
51,26
1,69 m
27,00
M
[ kN.m ]
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
26 / 37
EXERCÍCIO 07 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
2,5 m
21 kN
1,0 m
13 kN/m
2,5 m
4,0 m
17 kN
4,0 m
E , I → constantes
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
4
3
2,5 m
21 kN
1,0 m
13 kN/m
4,0 m
17 kN
2,5 m
ƒ
δ1R = 0
ϕ2R = 0
1
2
X1
X2
4,0 m
ESTÁTICA DAS ESTRUTURAS I
ƒ
PROF. IBERÊ
27 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica , Caso (1) e Caso (2) , com seus
respectivos gráficos de momento fletor :
13 kN/m
4
3
2,5 m
21 kN
1,0 m
CASO (0)
∑F
H
=0
+ 17 − 21 + RH 2 = 0
RH 2 = 4
∑M
2,5 m
4,0 m
17 kN
RV 2 = 15,62
V
ϕ20
1
=0
− RV 2 .4 + 17.2,5 + 13.4.2 − 21.4 = 0
∑F
δ10
1
=0
RV 1 + 15,62 − 13.4 = 0
RV 1 = 36,38
2
4,00 kN
15,62 kN
36,38 kN
4,0 m
42,50
3
3
4
20,00
4
4
26,00
42,50
1,00
3
0
4
0
1
M0
[ kN.m ]
2
2
21,00
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
28 / 37
4
3
X1 . CASO (1)
∑F
H
=0
5,0 m
1 − RH 2 = 0
RH 2 = 1
∑M
δ11
ϕ21
1
1,00 kN
RV 2 = 0
2
∑F
V
RV 1 = 0
5,00
5,00
3
3
1
=0
RV 1 + 0 = 0
0
4,0 m
5,00
=0
+ RV 2 .4 = 0
1,00 kN
0
1
4
M1
4
[ kN.m ]
2
5,00
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
29 / 37
4
3
X2 . CASO (2)
∑F
H
=0
5,0 m
RH 2 = 0
∑M
1
=0
+ RV 2 .4 − 1 = 0
RV 2 =
δ12
ϕ22
1
∑F
V
/4 kN
1
/4 kN
4
=0
RV 1 − 1 4 = 0
2
0
1
1
RV 1 =
1
4
1,00 kN.m
4,0 m
3
3
4
1,00
4
1,00
2
1,00
0
1
ƒ
M2
[ kN.m ]
Cálculo dos giros ϕ20 , ϕ21 , ϕ22 , e das flechas δ10 , δ11 , δ12 , por Castigliano :
δ 10 = ∫
M 0 .M 1
1
.dx =
. M 0 .M 1 .dx
E .I
E.I ∫
δ 10 =
s.i
s.i.k s.i
s.i.k ⎤
1 ⎡ s.i
.⎢ .(2.k1 + k 2 ) + .(k1 + k 2 ) −
+ .(2.k1 + k 2 ) −
E.I ⎣ 6
2
3
6
3 ⎥⎦
δ 10 =
1 ⎡ 2,5.42,5
4.5
8.26.5 1.21
5.20.5 ⎤
192,02
.⎢
.(2.5 + 2,5) +
.(42,5 + 1) −
.(2.5 + 4 ) −
=+
+
⎥
2
3
6
E .I ⎣ 6
3 ⎦
E.I
δ 11 = ∫
M 1 .M 1
s.i.k ⎞
1
1 ⎛ s.i.k
.dx =
.∫ M 1 .M 1 .dx =
.⎜
+ s.i.k +
⎟
E.I
E .I
E.I ⎝ 3
3 ⎠
ESTÁTICA DAS ESTRUTURAS I
δ 11 =
δ 12 = ϕ 21 =
ϕ 20 = ∫
ƒ
M 1 .M 2
1
1 ⎛ s.i.k s.i.k ⎞
.dx =
.∫ M 1 .M 2 .dx =
.⎜ −
−
⎟
E.I
E .I
E .I ⎝ 2
2 ⎠
1 ⎛ 4.5.1 5.1.5 ⎞
22,50
.⎜ −
−
⎟=−
E.I ⎝
2
2 ⎠
E.I
M 0 .M 2
s.i.k s.i.k s.i.k ⎤
1
1 ⎡ s.i
.dx =
.∫ M 0 .M 2 .dx =
.⎢− .(2.k1 + k 2 ) +
+
−
E.I
E.I
E.I ⎣ 6
3
2
2 ⎥⎦
1 ⎡ 4.1
4.1.26 5.20.1 1.21.1⎤
44,50
=+
.⎢−
.(2.1 + 42,5) +
+
−
⎥
E.I ⎣ 6
3
2
2 ⎦
E .I
ϕ 22 = ∫
ϕ 22 =
30 / 37
5.5.5 ⎞
183,33
1 ⎛ 5.5.5
.⎜
+ 4.5.5 +
⎟=+
E.I ⎝ 3
3 ⎠
E.I
δ 12 = ϕ 21 = ∫
ϕ 20 =
PROF. IBERÊ
M 2 .M 2
1
1 ⎛ s.i.k
⎞
.dx =
.∫ M 2 .M 2 .dx =
.⎜
+ s.i.k ⎟
E.I
E.I
E.I ⎝ 3
⎠
1 ⎛ 4.1.1
6,33
⎞
.⎜
+ 5.1.1⎟ = +
E .I ⎝ 3
E.I
⎠
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) + X2 . ( 2 ) ⇒
192,02 183,33
22,50
⎧
⎪⎪0 = E.I + E.I . X 1 − E.I . X 2
⎨
⎪0 = 44,50 − 22,50 . X + 6,33 . X
1
2
⎪⎩
E.I
E.I
E.I
⎧δ 1R = δ 10 + X 1 .δ 11 + X 2 .δ 12
⎨
⎩ϕ 2 R = ϕ 20 + X 1 .ϕ 21 + X 2 .ϕ 22
⎧− 192,02 = 183,33. X 1 − 22,50. X 2
⇒ ⎨
⎩− 44,50 = −22,50. X 1 + 6,33. X 2
⎧ X = −3,388
⇒ ⎨ 1
⎩ X 2 = −19,074
∴ podemos assim afirmar que o momento reativo no engaste (2) assume o valor X2 . 1,0 kN.m , ou
seja, vale 19,07 kN.m ; e a reação horizontal no apoio (1) assume o valor X1 . 1,0 kN, ou seja , vale
3,39 kN. O sinais negativos indicam que o momento e a reação horizontal assumem o sentido
contrário ao escolhido na proposição dos casos .
ƒ
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
RV 1 = 36,38 − 3,388.0 − 19, 074. ( + 1 4 ) = 31, 61 kN
RH 2 = 4, 00 − 3,388. ( −1) − 19, 074.0 = 7,39 kN
RV 2 = 15, 62 − 3,388.0 − 19, 074. ( − 1 4 ) = 20,39 kN
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
31 / 37
13,61
13,61
–
31,61
20,39
–
–
N
[ kN ]
31,61
20,39
31,61
+
13,61
13,61
–
+
7,39
–
20,39
13,61
3,39
13,61
–
2,43 m
+
V
3,39
[ kN ]
7,39
25,55
3,14
25,55
3,14
12,86
10,49
8,48
1,57 m
M
19,07
[ kN.m ]
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
32 / 37
EXERCÍCIO 08 : Na estrutura esquematizada abaixo , calcular as reações de apoio e
os diagramas de esforços internos solicitantes :
I
2,0 m
20 kN/m
I
40 kN
2,0 m
6,0 m
I
2.I
E → constante
2,0 m
4,0 m
Resolução :
Definição da estrutura equivalente e numeração (Caso Real) :
40 kN
20 kN/m
40 kN.m
3
2,0 m
4
I
40 kN
2.I
δ2R = 0
X2
ϕ1R = 0
1
X1
4,0 m
2,0 m
I
6,0 m
ƒ
2
ESTÁTICA DAS ESTRUTURAS I
33 / 37
Desmembramento da estrutura em Caso (0) – Isostática Básica , Caso (1) e Caso (2) , com seus
respectivos gráficos de momento fletor :
40 kN
CASO (0)
20 KN/m
∑F
40 kN.m
3
H
R H 1 = 40
40 kN
∑M
2,0 m
I
2.I
δ20
1
=0
− RV 2 .4 − 40.4 + 20.4.2 + 40.4 + 40 = 0
RV 2 = 50
2
∑F
V
=0
RV 1 + 50 − 20.4 − 40 = 0
50 KN
ϕ10
=0
− 40 + RH 1 = 0
2,0 m
4
I
6,0 m
ƒ
PROF. IBERÊ
RV 1 = 70
1
40 KN
70 KN
240,00
4,0 m
4
3
3
4
40,00
240,00
0
120,00
4
3
1
M0
[ kN.m ]
2
80,00
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
34 / 37
X1 . CASO (1)
3
∑F
2,0 m
4
I
H
RH 1 = 0
∑M
δ21
1
RV 2 =
2
∑F
/4 kN
RV 1 =
1
1
/4 kN
4,0 m
1,00
4
1,00
3
4
3
0
2
M1
1,00
1
4
RV 1 − 1 4 = 0
1
1,00
1
=0
V
0 ϕ11
=0
+ RV 2 .4 − 1 = 0
2,0 m
6,0 m
I
2.I
=0
[ kN.m ]
1
4
ESTÁTICA DAS ESTRUTURAS I
PROF. IBERÊ
35 / 37
X2 . CASO (2)
3
2,0 m
4
I
∑F
H
RH 1 − 1 = 0
RH 1 = 1
2,0 m
6,0 m
I
δ22
2.I
∑M
2
1
=0
− RV 2 .4 + 1.2 = 0
1,00
RV 2 = 0,5
0,5 kN
ϕ12
=0
∑F
V
1
=0
− RV 1 + 0,5 = 0
1,00 kN
RV 1 = 0,5
0,5 kN
4,0 m
3
6,00
4,00
4
4
3
4,00
6,00
2
M2
[ kN.m ]
1
ƒ
Cálculo dos giros ϕ10 , ϕ11 , ϕ12 , e das flechas δ20 , δ21 , δ22 , por Castigliano :
3
2
1
1
ϕ10 =
.∫ M 0 .M 1 .dx +
.∫ M 0 .M 1 .dx = 1 .⎛⎜ s.i.k ⎞⎟ + 1 .⎡⎢ s.i .(2.k1 + k 2 ) − s.i.k ⎤⎥
2.E.I 1
E.I 3
2.E.I ⎝ 2 ⎠ E.I ⎣ 6
3 ⎦
ϕ 10 =
1 ⎛ 6.240.1 ⎞ 1 ⎡ 4.1
4.40.1⎤ 2120
.⎜
.⎢ .(2.240 + 120) −
=
⎟+
2.E.I ⎝ 2 ⎠ E.I ⎣ 6
3 ⎥⎦ 3.E.I
1
1
1
1 ⎛ s.i.k ⎞
ϕ11 =
.∫ M 0 .M 1 .dx +
.∫ M 0 .M 1 .dx =
.(s.i.k ) +
.⎜
⎟
E.I 3
E .I ⎝ 3 ⎠
2.E.I 1
2.E.I
3
ϕ11 =
2
1
1 ⎛ 4.1.1 ⎞
13
.(6.1.1) +
.⎜
⎟=
2.E .I
E.I ⎝ 3 ⎠ 3.E.I
ESTÁTICA DAS ESTRUTURAS I
ϕ12 = δ 21
36 / 37
1
1
1 ⎛ s.i.k ⎞ 1 ⎡ s.i
⎤
.∫ M 1 .M 2 .dx +
.∫ M 1 .M 2 .dx =
.⎜ −
.⎢− .(2.k1 + k 2 )⎥
=
⎟+
2.E.I 1
E.I 3
2.E.I ⎝ 2 ⎠ E.I ⎣ 6
⎦
3
ϕ12 = δ 21 =
δ 20
PROF. IBERÊ
2
1 ⎛ 6.6.1 ⎞ 1 ⎡ 4.1
59
⎤
.⎜ −
.⎢−
.(2.6 + 4 )⎥ = −
⎟+
2.E.I ⎝
2 ⎠ E .I ⎣ 6
3.E.I
⎦
3
2
1
1
=
.∫ M 0 .M 2 .dx +
. M 0 .M 2 .dx
2 .E .I 1
E.I ∫3
δ 20 =
1 ⎛ s.i.k ⎞ 1 ⎡ s.i
s
s.i
⎤
.⎜ −
.⎢ .(k1 + k 2 ) − .(2.i1 .k1 + i1 .k 2 + i2 .k1 + 2.i2 .k 2 ) − .(2.k1 + k 2 )⎥
⎟+
2.E.I ⎝ 3 ⎠ E.I ⎣ 3
6
6
⎦
δ 20 =
2.80
1 ⎛ 6.6.240 ⎞ 1 ⎡ 4.40
4
⎤
.(2.4 + 2)⎥
.⎜ −
.⎢
.(6 + 4) − .(2.6.240 + 240.4 + 120.6 + 2.4.120) −
⎟+
6
6
2.E.I ⎝
3 ⎠ E.I ⎣ 3
⎦
δ 20 = −
14560
3.E.I
3
2
δ 22 =
1
1
.∫ M2 .M2 .dx + .∫ M2 .M2 .dx = 1 .⎛⎜ s.i.k ⎞⎟ + 1 .⎡⎢ s.i.k + s .(2.i1 .k1 + i1.k 2 + i2 .k1 + 2.i2 .k 2 )⎤⎥
2.E.I 1
E.I 3
2.E.I ⎝ 3 ⎠ E.I ⎣ 3
6
⎦
δ 22 =
1 ⎛ 6.6.6 ⎞ 1 ⎡ 4.4.4 4
⎤ 476
.⎜
.⎢
+ .(2.6.6 + 6.4 + 4.6 + 2.4.4)⎥ =
⎟+
2.E.I ⎝ 3 ⎠ E.I ⎣ 3
6
⎦ 3.E.I
ƒ
Montagem sistema linear com equação de compatibilidade :
( R ) = ( 0 ) + X1 . ( 1 ) + X2 . ( 2 ) ⇒
⎧ϕ 1R = ϕ 10 + X 1 .ϕ 11 + X 2 .ϕ 12
⎨
⎩δ 2 R = δ 20 + X 1 .δ 21 + X 2 .δ 22
2120
13
59
⎧
⎪⎪0 = 3.E.I + 3.E.I . X 1 − 3.E.I . X 2
⎨
⎪0 = − 14560 − 59 . X + 476 . X
1
2
⎪⎩
3.E.I 3.E.I
3.E.I
⎧− 2120 = 13. X 1 − 59. X 2
⇒ ⎨
⎩14560 = −59. X 1 + 476. X 2
⎧ X = −55,441
⇒ ⎨ 1
⎩ X 2 = +23,716
∴ podemos assim afirmar que o momento reativo no engaste (1) assume o valor X1 . 1,0 kN.m ,
ou seja, vale 55,44 kN.m , sendo que o sinal negativo indica que o momento assume sentido
contrário ao escolhido na proposição dos casos ; e a reação horizontal no apoio (2) assume o valor
X2 . 1,0 kN, ou seja , vale 23,72 kN , o sinal positivo indica que a reação horizontal assume o sentido
o escolhido na proposição dos casos .
ESTÁTICA DAS ESTRUTURAS I
ƒ
PROF. IBERÊ
37 / 37
Cálculo das Reações de Apoio e Diagrama de Esforços Internos Solicitantes
RV 1 = 70, 00 − 55, 441.0, 25 + 23, 716. ( −0,50 ) = 44, 28 kN
RH 1 = 40, 00 − 55, 441.0 + 23, 716. ( −1, 00 ) = 16, 28 kN
RV 2 = 50, 00 − 55, 441. ( −0, 25 ) + 23, 716.0,50 = 75, 72 kN
16,28
16,28
44,28
40,00
0
–
44,28
+
75,72
+
16,28
16,28
–
+
–
35,72
–
16,28
23,72
–
–
75,72
2,21 m
23,72
N
[ kN ]
V
44,28
16,28
40,00
42,24
25,12
42,24
14,88
6,78
2,21 m
47,44
M
55,44
[ kN.m ]
[ kN ]