Campo magnético no interior de espiras e bobinas Lei de Biot

Centro de Ensino Médio Setor Leste
Apostila de Física – Terceiro ano – Segundo Bimestre
Prof. Flávio Ambrósio
Campo magnético no interior de espiras e bobinas
elétrica e os quatro dedos girando em torno do fio dando o sentido do
campo magnético.
Lei de Biot-Savart
A Lei de Biot-Savart expressa o comportamento do campo magnético
nas proximidades de um fio condutor qualquer e pode ser utilizada para
calcular o campo magnético no centro de uma espira circular, com mostra
desenvolvimento matemático abaixo
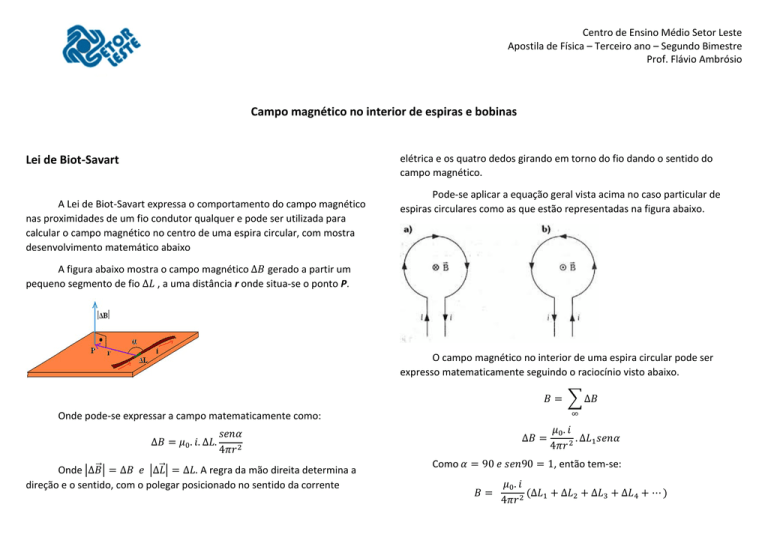
Pode-se aplicar a equação geral vista acima no caso particular de
espiras circulares como as que estão representadas na figura abaixo.
A figura abaixo mostra o campo magnético ∆𝐵 gerado a partir um
pequeno segmento de fio ∆𝐿 , a uma distância r onde situa-se o ponto P.
O campo magnético no interior de uma espira circular pode ser
expresso matematicamente seguindo o raciocínio visto abaixo.
𝐵 = ∑ ∆𝐵
∞
Onde pode-se expressar a campo matematicamente como:
𝑠𝑒𝑛𝛼
∆𝐵 = 𝜇0 . 𝑖. ∆𝐿.
4𝜋𝑟 2
⃗ | = ∆𝐵 𝑒 |∆𝐿
⃗ | = ∆𝐿. A regra da mão direita determina a
Onde |∆𝐵
direção e o sentido, com o polegar posicionado no sentido da corrente
∆𝐵 =
𝜇0 . 𝑖
. ∆𝐿1 𝑠𝑒𝑛𝛼
4𝜋𝑟 2
Como 𝛼 = 90 𝑒 𝑠𝑒𝑛90 = 1, então tem-se:
𝐵=
𝜇0 . 𝑖
(∆𝐿1 + ∆𝐿2 + ∆𝐿3 + ∆𝐿4 + ⋯ )
4𝜋𝑟 2
(∆𝐿1 + ∆𝐿2 + ∆𝐿3 + ∆𝐿4 + ⋯ ) = 2𝜋𝑟
O campo magnético no centro de uma espira circular de raio r pode
ser expresso pela equação abaixo.
𝐵=
𝜇0 . 𝑖
2𝑟
Pode-se observar que o campo magnético surge em toda a
vizinhança de das espiras. Observa-se ainda que as linhas que representam o
campo magnético são mais concentradas na parte central do interior da
bobina.
No interior da bobina tem-se um campo uniforme com valor
constante calculado pela equação abaixo.
𝐵 = 𝜇0 .
𝑁
.𝑖
𝐿
Campo magnético no interior de uma bobina longa (SOLENÓIDE)
Onde N é o número de espiras e L é comprimento da bobina. Pode-se
𝑵
definir 𝜼 = 𝑳 como a densidade de espiras da bobina e sendo assim pode
escrever:
𝐵 = 𝜇0 . 𝜂. 𝑖
O sentido campo magnético no interior da bobina longa é definido
A figura acima representa uma bobina constituída por uma sequência
de esperas circulares continuamente interligadas, pelas quais pode passar
uma corrente elétrica.
A figura abaixo mostra um campo magnético gerado por uma
corrente elétrica que flui pelo fio que compõe a bobina.
pela regra da mão direita, como foi feito para a espira circular na espira
circular.
Exercícios
Preencha as tabelas abaixo utilizando as leis e definição expressas
através das equações matemáticas. A tabela 1 trabalho com o campo
magnético nas vizinhas de um fio reto infinito, uma espira circular e uma
bobina longa. A tabela 2 trabalha com Lei de Faraday e a expressão da força
magnética.
Tabela 1- Campo magnético
Fio reto
𝐵=
Espira
circular
𝜇0 . 𝑖.
2𝜋𝑑
𝑇.𝑚
)
𝐴
B
(T)
𝐵=
d
(m)
i
(A)
a
0,01
10
b
0,0025
1,2
d
e
f
1
5
i
𝐵 = 𝜇0 .
𝜇0 = 4𝜋. 10−7 (
c
Bobina longa
(solenoide)
B
(T)
0,5
r
(m)
i
(A)
0,001
0,003
0,55
20
0,1
𝑅=
10
1
0,005
𝜇0 . 𝑖.
2𝑟
5
0,15
10
B
(T)
V R
𝑁
.𝑖
𝑙
𝑉
𝑖
N
l
(m)
i
(A)
110
100
0,1
15
15
200
0,1
15
1,25
0,1
400
0,2
2,0
0,2
600
0,2
50
0,3
1200
10
0,4
1800
V
(V)
R
(Ω)
15
6
12
15
30
20
0,5
3
Tabela 2
* Considere o campo magnético constante e a variação (𝐵𝑓 − 𝐵𝑖 ) apenas em função da rotação da bobina.
** A posição inicial da bobina deve ser paralela ou perpendicular ao campo magnético.
Lei da indução de Faraday
Força de magnética
B
Δ𝜙𝐵
𝑉=−
Δ𝑡
** 𝜃 → Ângulo
de rotação da
espira, medido
sempre a partir
da posição inicial.
v
𝜙𝐵 = 𝐵. 𝐴
A
𝐵𝑖
(T)
𝐵𝑓
(T)
A
( m2 )
∆𝑡
(s)
a
1,0
0,0
0,01
b
0,0
1,0
0,025
0,0
15
0,03333
10
0,02
V
(V)
c
-5,0
d
-1,5
e
f
3,0
5,0
∆𝜃
(o)
F
⃗ )
𝐹𝑚 = 𝑞(𝑣 × 𝐵
v
⃗ |. 𝑠𝑒𝑛(𝛼)
|𝐹𝑚 | = 𝑞. |𝑣|. |𝐵
B
F
(N)
𝛼
q
(C)
v
( m/s )
B
(T)
(o)
0,01
1
100
1
90
1,0
2
80
1,5
90
3
33
2
90
3
60
90
1000
10
5
0,04
0,1
90
500
0,05
0,05
90
300
1500
500
45
0,33
30