determinação da velocidade de propagação da luz no ar, água e

DETERMINAÇÃO DA VELOCIDADE DE PROPAGAÇÃO DA
LUZ NO AR, ÁGUA E NUMA RESINA EPÓXICA
OBJECTIVO
Esta experiência permite determinar a velocidade de propagação da luz no ar, e noutros meios
materiais.
1. INTRODUÇÃO
O princípio e funcionamento desta experiência é igual ao utilizado para determinar a
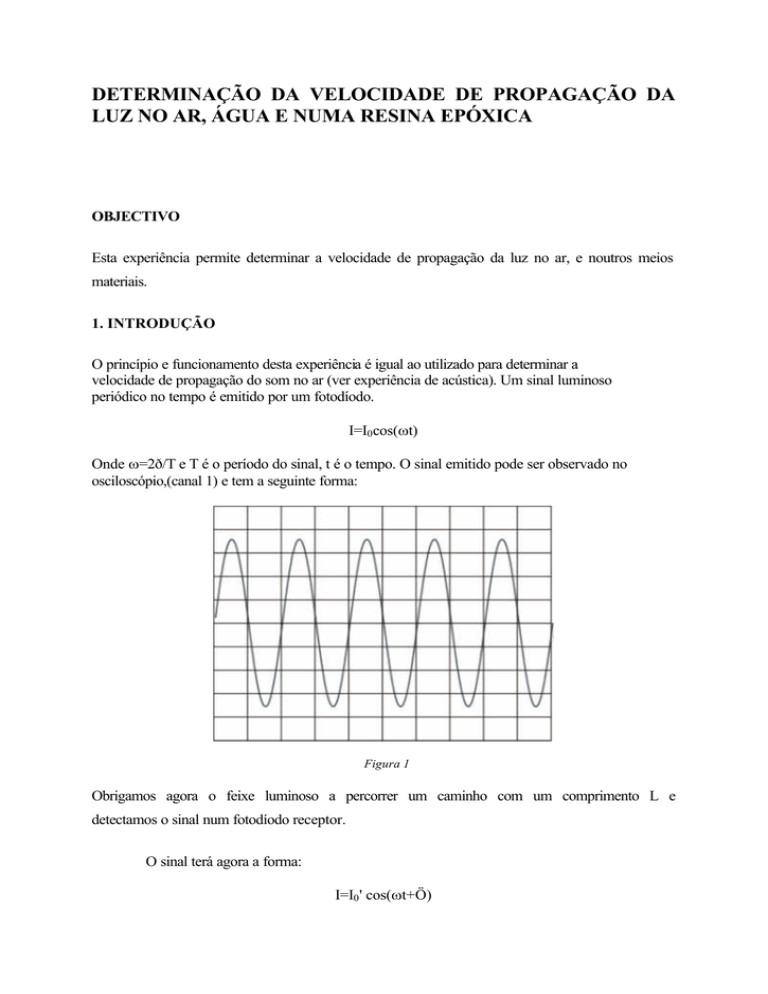
velocidade de propagação do som no ar (ver experiência de acústica). Um sinal luminoso
periódico no tempo é emitido por um fotodíodo.
I=I0 cos(ωt)
Onde ω=2ð/T e T é o período do sinal, t é o tempo. O sinal emitido pode ser observado no
osciloscópio,(canal 1) e tem a seguinte forma:
Figura 1
Obrigamos agora o feixe luminoso a percorrer um caminho com um comprimento L e
detectamos o sinal num fotodíodo receptor.
O sinal terá agora a forma:
I=I0 ' cos(ωt+Ö)
onde Ö corresponde à diferença de fase do sinal introduzida devido à luz ter percorrido o
espaço L num tempo finito a uma velocidade c. Podemos agora comparar a forma do sinal
sinusoidal recebido no fotodíodo receptor com o sinal emitido, colocando para isso o sinal do
fotodíodo receptor no canal 2 do osciloscópio e observando os dois sinais em simultâneo.
Figura 2
O desfasamento no tempo (∆T) que observa entre os dois sinais corresponde ao tempo que a
luz demora a percorrer o caminho definido pelos espelhos, desde que saiu do fotodíodo
emissor até que chegou ao fotodíodo receptor.
Temos assim:
Ä T=L/c,
c= L/( Ä T)
2. EQUIPAMENTO
1- fotodíodo emissor(50MHz), e fotodíodo receptor
2- calha óptica
3- 2 lentes para focar o feixe no espelho e no fotodíodo receptor
4- jogo de 2 espelhos móveis para deflectir o feixe
5- osciloscópio com dois canais
6- um tubo fechado com extremidades em vidro, com ar no interior
7- um tubo fechado com extremidades em vidro, com água no interior
8- um bloco de resina acrílica
Figura 3
EXPERIÊNCIA I – cAr
a) - Ligue o fotodíodo emissor e observe o sinal emitido no canal 1 do osciloscópio.
Determine a frequência do sinal observado no osciloscópio. Como compara o valor obtido
com os 50 MHz indicados pelo fabricante do gerador de sinal?
b) - Coloque o jogo de espelhos na extremidade da calha óptica. Utilize as lentes para focar o
feixe no espelho e no fotodíodo receptor. TENHA PACIÊNCIA ISTO PODE
DEMORAR. Use um papel branco para auxiliar na detecção do feixe e obtenha um
ambiente escurecido para melhorar a sua qualidade visual.
Observe os dois sinais no osciloscópio. Existe algum desfasamento entre os sinais?
Comente.
Sugestão:
Acertando a posição da lente junto ao emissor, obtenha um feixe de raios
paralelos a incidir no primeiro espelho, com o suporte dos espelhos colocados
ao fundo da calha. Para alinhar o feixe no percurso de regresso, utilize os
parafusos de ajuste dos espelhos de forma a fazer incidir o feixe de luz sobre a
lente colocada junto do fotodíodo receptor. Acerte a posição desta lente de
forma a fazer convergir o feixe de luz sobre o fotodíodo (corresponde a obter a
intensidade máxima do sinal no osciloscópio que deve ser no mínimo de
100mV).
Nota:
Se tapar o emissor, vai observar que o sinal do receptor (no osciloscópio) não é
nulo. O que está observar é ruído interno do gerador.
c) - Reposicione os espelhos na origem. Coloque o osciloscópio no modo XY. Deve agora
observar uma elipse no caso de haver um pequeno desfasamento entre os sinais. Se
estiverem em fase Φ=2nπ, onde n=0,1,2...) a elipse degenera num segmento de recta que
bissecta os quadrantes ímpares. Se estiverem em oposição de fase, (Φ=(2n+1)ð) a elipse
degenera num segmento de recta que bissecta os quadrantes pares. O gerador de sinal
tem um potenciómetro que lhe permite ajustar a fase do sinal recebido em relação ao
sinal emitido.
Com o osciloscópio no modo XY rode o potenciómetro até que a elipse degenere num
segmento de recta que bissecte os quadrantes impares. Saia do modo XY e confirme que
os sinais estão em fase. Não altere mais neste potenciómetro até ao fim da experiência.
d) - Agora que tem um bom sinal no receptor, coloque novamente o osciloscópio no modo
XY, e mova o jogo de espelhos com muito cuidado para não desfocar o feixe reflectido,
de modo a que a elipse observada degenere num segmento de recta nos quadrantes pares
( Nota: Só se a intensidade dos dois canais for a mesma é que o segmento de recta
bissecta os quadrantes). Está agora em oposição de fase. Observe os dois canais
separadamente. Qual o desfasamento em tempo? Qual o erro cometido nesta medida?
(deve corresponder a meio período, T/2) Indique a escala de tempo que usou no
osciloscópio.
Ä t= (
±
) x10-9 s
Tome nota da distância entre a origem e a nova posição do suporte dos espelhos
d0 =
±
mm;
∆d=
±
d1 =
±
mm
mm
Determine de quanto pode mover a base dos espelhos em torno da posição previamente
determinada, sem notar alteração do desfasamento entre os sinais no osciloscópio. Isto
dá-lhe uma estimativa da incerteza na determinação da posição correspondente à
oposição de fase. (∆d).
e) - Calcule a velocidade de propagação da luz utilizando a expressão 1:
L=
Ät= (
car =
(
(
±
±
±
) cm
) x 10e- 9 s
) x 10e+8 m/s
Observando a figura 3 justifique porque pode não considerar a distância entre os espelhos
para o cálculo da distância.
f) - Como compara o valor obtido com o valor que conhece para a velocidade de propagação
da luz no vazio?
EXPERIÊNCIA II - cágua
a) - Coloque agora o tubo vazio com as extremidades em vidro entre o fotodíodo emissor e o
jogo de espelhos. Observe o que acontece ao sinal recebido no receptor. Comente a sua
observação. Com o osciloscópio no modo XY, ajuste ligeiramente a posição da base dos
espelhos de modo a ter os dois sinais em oposição de fase.
Podemos agora substituir o tubo vazio pelo tubo com água. Saia do modo XY e observe
o sinal no fotodíodo receptor.
O sinal agora recebido no fotodíodo é muito fraco e tem que optimizar a focagem e o
alinhamento de modo a observar inequivocamente o sinal luminoso que atravessa o tubo
com água. Coloque os dois sinais com amplitudes semelhantes utilizando as escalas do
osciloscópio e regresse ao modo XY. Observará uma elipse, correspondente ao novo
desfasamento devido ao atraso que a luz tem ao ter que percorrer o novo meio - a água.
Desloque a base do espelho até determinar a nova posição de oposição de fase.
±
d2 =
mm
±
d3 =
Lar=
mm
Lágua =
O desfasamento total é devido aos desfasamentos introduzidos pelo percurso no ar e na água.
Temos assim,
T / 2 = ( Lar / Car ) + ( Lagua / Cagua )
donde:
Cagua =
Lagua
(T / 2) − ( Lar / Car )
=
m/s
O índice de refracção da água em relação ao vazio é dado pela razão entre a velocidade e
propagação no vazio, e na água
C AGUA, AR = ( C AR / C AGUA ) =
m/ s
EXPERIÊNCIA III (resina)
a) - Retire o tubo de água e coloque os espelhos na posição de oposição de fase para o ar.
Coloque o bloco de resina utilizando a dimensão maior e observe, com o osciloscópio no
modo XY, que o segmento de recta obtido para a água degenerou numa elipse pois o
atraso obtido ao atravessar o bloco de resina é diferente do atraso obtido ao atravessar o
tubo de água.
b) - Determine e registe agora a nova posição de oposição de fase:
d4 =
±
mm
d5 =
±
mm
Lar=
Lágua =
c) - Em oposição de fase, ÄT=T/2. Neste espaço de tempo a luz percorre dois meios com
velocidades diferentes,
∆T / 2 = ( LAR / c AR ) + ( LRES / c RES ) =
cRES =
L AR =
LRESINA =
LRES
=
(T /2) − ( LAR / cAR )
Efectue este cálculo e determine a velocidade de propagação da luz na resina. Qual o índice
de refracção da resina em relação ao ar?
d) - Vai agora determinar o índice de refracção da resina por um método muito simples.
Coloque o bloco de resina em cima de uma folha de papel branco. Marque no papel a
trajectória de um raio luminoso que atravesse a bloco de resina. Para tal comece por
escolher dum dos lados do bloco uma direcção traçando uma linha recta a lápis. Espete
dois alfinetes verticais ao longo dessa linha. Espreite agora do outro lado do bloco tente
ver os dois alfinetes sobrepostos e coloque outros dois alinhados com eles do novo lado.
Marque então a lápis a trajectória completa do raio. Faça pelo menos três determinações.
Meça os ângulos de incidência e transmissão para cada caso:
Figura 4
Figura 5
Nota: Obtém-se melhores resultados para ângulos de incidência grandes do que para ângulos
de incidência pequenos.
Utilize a lei de Snell para calcular o índice de refracção da resina:
nar sin(i) = nres sin(t )
sendo n ar = 1 e i e t os ângulos que o alinhamento de cada par de alfinetes faz com a normal
ao bloco de resina, antes e depois de nele ter penetrado. Utilize pelo menos 3 medidas para
ângulos de incidência e transmissão diferentes. Expresse o índice de refracção em função do
parâmetro de ataque (distância entre as duas rectas paralelas definidas pelos alfinetes).
Preencha a tabela seguinte, e faça o gráfico sin(i) versos sin(t). Compare com o valor obtido
no ponto 4 anterior.
Ângulo
incidente
sin (i)
sin(t)
nres/nar