circuito

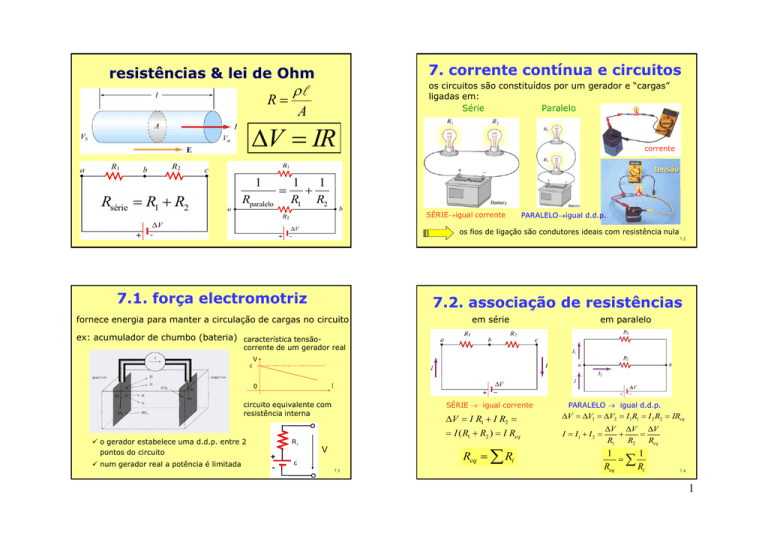
7. corrente contínua e circuitos
resistências & lei de Ohm
R

os circuitos são constituídos por um gerador e “cargas”
ligadas em:
Série
Paralelo
A
V  IR
corrente
tensão
1
Rsérie  R1  R2
Rparalelo
1
1


R1 R2
SÉRIEigual corrente
PARALELOigual d.d.p.
os fios de ligação são condutores ideais com resistência nula
1
7.1. força electromotriz
7.2
7.2. associação de resistências
fornece energia para manter a circulação de cargas no circuito
em série
em paralelo
ex: acumulador de chumbo (bateria) característica tensão-
corrente de um gerador real
e
V
I
0
circuito equivalente com
resistência interna
 o gerador estabelece uma d.d.p. entre 2
pontos do circuito
 num gerador real a potência é limitada
Ri
+
-
SÉRIE  igual corrente
V  I R1  I R2 
 I ( R1  R2 )  I Req
I  I1  I 2 
Req   Ri
V
e
7.3
PARALELO  igual d.d.p.
V  V1  V2  I1 R1  I 2 R2  IReq
V V V


R1
R2
Req
1
1

Req
Ri
7.4
1
exemplo de cálculo sobre um circuito
7.3. leis de Kirchoff
qual é a corrente fornecida pelo gerador de fem e?
lei dos nós
lei das malhas
conservação da carga
campo eléctrico é conservativo
I1
I2
I
aplicar a lei dos nós I  I1  I 2
a soma das correntes que
chegam a um nó é igual à
soma das correntes que saem
I
entrar
  I sair
aplicar a lei das malhas
2e  RI1  RI 2  0
a soma das d.d.p.
é nula sobre uma
malha
 Vi  0
i
7.5
passos para resolver um problema
de circuitos
1.
2.
3.
4.
5.
6.
7.
simplificar o circuito é,
quase sempre, vantajoso
RI 2  e  0
resolver o sistema de equações
e
I2 
2e  RI  e  e  0
R
I1  I 
e
I 0
R
7.6
problema: circuito
Determinar os valores lidos nos aparelhos. Todas as
resistências são R e as baterias têm f.e.m. e
“endireitar” o circuito (fazer rectângulos)
simplificar as resistências em série/paralelo
atribuir correntes aos ramos (arbitrárias)
escrever as leis dos nodos
atribuir sentido de circulação para as malhas
escrever as equações das malhas (1 por malha)
Resolver o sistema de equações
6.7
MAIS DIFÍCIL
MAIS FÁCIL
6.8
2
medida da corrente
medida da diferença de potencial
um voltímetro deve ser ligado em paralelo com o
elemento de circuito através do qual se quer
medir a diferença de potencial
1
Refectiva

um amperímetro deve ser ligado em série com o
elemento do circuito através do qual queremos
medir a corrente
1
1

R RVoltimetro
Refectiva  R  Ramperímetro
0
os voltímetros devem ter uma resistência elevada de
forma a não afectarem demasiado o circuito
0
7.9
os amperímetros têm uma resistência muito
baixa de forma a não afectarem demasiado o
circuito
medida da resistência
7.4. circuitos RC
um ohmímetro deve ser ligado em paralelo em
relação ao elemento do circuito do qual queremos
medir a resistência
carga ou descarga de condensadores
 quando o fluxo de corrente entra na armadura
positiva do condensador,
I 
carga do condensador
estamos a medir R1
os ohmímetros aplicam uma tensão e medem a corrente que
passa
tipicamente eles não funcionam se a resistência está
7.11
alimentada (ligada a uma bateria)
7.10
dQ
dt
 quando o fluxo de corrente sai da armadura
positiva do condensador,
I 
descarga do condensador
dQ
dt
a armadura positiva do condensador é a que está a
maior potencial
7.12
3
variação da carga no condensador e da
corrente no circuito
7.4.1. carga de um condensador
1. sinal da carga das armaduras
3. equação da(s) malha(s)
4. integração da equação
RD 
NÃO PASSA
CORRENTE!
dQ
dt
i
2. sentido da corrente
Q
 Ri  e  0
C
R
1
1
0D
C
RC
dQ Q
 e
dt C
Q(t )  Ae

1
t
RC
 IP
t    i  0: Q()  Ce  IP  Ce
descarregado em t  0 : Q(0)  0  A  IP  Ce
1

t 

Q(t )  Ce 1  e RC 


Q  Ce 1  et / RC


I
dQ e  t / RC
 e
dt
R
RC é a constante de tempo e tem unidades de segundos
7.13
7.14
variação da tensão e da corrente no circuito
durante a descarga do condensador
7.4.2. descarga de um condensador
1. sinal da carga das armaduras
i
2. sentido da corrente
3. equação da(s) malha(s) Ri 
dq
dt
q
0
C
I0 
Q
RC
4. integração da equação  R dq  q  0
RD 
NÃO PASSA
CORRENTE!
mas há carga no
condensador
1
1
0D
C
RC
dt
C
q(t )  Ae

1
t
RC
é uma equação homogénea, em que
IP = 0
q(t  0)  Q  A  Q
q(t )  Qe

1
t
RC
7.15
V (t ) 
q(t ) Q  t / RC
 e
C
C
I 
dq
Q

e  t / RC
dt RC
a energia armazenada no condensador é libertada na resistência
7.16
sob a forma de calor
4
integração das equações diferenciais
lineares - método do polinómio em D
os fenómenos transitórios em circuitos eléctricos podem
ser tratados por equações diferenciais lineares de primeira
ou segunda ordem
equação do circuito
solução da forma
passagem a polinómio
a solução depende do valor de
D1
o IP calcula-se a partir das
condições de regime permanente
em que as derivadas são nulas
a outra constante determina-se
a partir das condições iniciais
Q
 V  Q()  CV  IP
C
Q(t  0)
ou
i(t  0)
dQ Q
exemplo: R
 V
dt C
integral geral = int. geral eq.
homogénea + int. particular
RD 
1
 0  raíz D1
C
Q (t )  Ae D1t  IP
7.17
7.18
Fonte de tensão
7.5. Teoremas dos circuitos lineares
Uma fonte de tensão é qualquer dispositivo que produz uma força
electromotriz (f.e.m.) entre os seus terminais
Técnicas para a análise e resolução de circuitos eléctricos lineares
Um exemplo de fonte de tensão é uma bateria comum
Só vamos estudar os teoremas da Sobreposição, de Thévenin e de
Norton
Na teoria dos circuitos eléctricos uma fonte de tensão é
equivalente a uma fonte de corrente
7.19
Uma fonte de tensão ideal, V, alimenta uma resistência R, e cria
uma corrente I
7.20
5
Fonte de Corrente
Uma fonte de tensão ideal não tem resistência interna e consegue
fornecer toda a corrente que fôr pedida (que tende para infinito
quanto a resistência de carga tende para 0)
Uma fonte ideal de corrente, I, alimenta uma resistência, R, e
cria uma diferença de potencial V
Não existem fontes ideais de tensão, mas podem aproximar-se a
uma em intervalos limitados de corrente
Será ideal se não possuir resitência interna e fornecer uma
corrente constante independentemente da resistência de carga
Uma fonte de corrente é um dispositivo eléctrico ou electrónico
que produz ou consome corrente eléctrica
É equivalente a uma fonte de tensão
7.21
7.22
Vamos aplicar o teorema da sobreposição ao seguinte circuito:
7.5.1. Teorema da sobreposição
Em qualquer circuito linear a intensidade de corrente num dado
ramo, e a queda de tensão entre dois nodos, devidas às fontes de
tensão e de corrente desse circuito, são iguais, respectivamente, às
somas das correntes e às somas das tensões que seriam
produzidas quando cada um dos geradores fosse ligado
separadamente e os outros substituídos pelas suas resistências
internas
Como temos duas fontes de potência no circuito, temos de calcular
dois conjuntos de valores para as quedas de tensão e para as
correntes. Um para o circuito apenas com a fonte de 28 V:
7.23
7.24
6
E outro para o circuito com a bateria de 7 V:
7.5.2. Teorema de Thévenin
Qualquer circuito linear contendo fontes de tensão ou de corrente
e resistências pode ser substituído, para efeitos do cálculo de outro
circuito a que está ligado por dois terminais, por uma fonte de
tensão em série com uma resistência
A f.e.m. do gerador equivalente é igual à queda de tensão entre os
dois terminais quando em circuito aberto
Quando se redesenha o circuito, para análise de componentes em
série e paralelo, com apenas uma fonte, todas as outras fontes de
tensão são substituídas por curto-circuitos e as fontes de corrente
por circuitos abertos
A resistência é igual à resistência medida entre esses dois terminais
quando as fontes de potência do circuito são substituídas pelas
suas resistências internas
Fontes de tensão ideais são substituídas por curto-circuitos e fontes
de corrente ideias por circuitos abertos
7.25
Exemplo de aplicação do teorema de Thévenin a
este circuito
7.26
Etapa 2: Cálculo da Tensão de Circuito Aberto
a tensão de circuito aberto pode ser calculada usando a seguinte
abordagem:
Etapa 1: Cálculo da resistência de Thévenin
A resistência de Thévenin pode ser obtida pela resistência equivalente
vista dos pontos AB
Equivalente de Thévenin
7.27
7.28
7
7.5.3. Teorema de Norton
Exemplo de aplicação do teorema de Norton a
este circuito
Qualquer circuito linear contendo fontes de tensão ou de corrente
e resistências pode ser substituído, para efeitos do cálculo de outro
circuito a que está ligado por dois terminais, por uma fonte de
corrente em paralelo com uma resistência
A intensidade de corrente da fonte equivalente é igual à
intensidade de corrente de curto-circuito entre os dois terminais
Etapa 1: Calcular a corrente equivalente em
circuito fechado
A resistência é igual à resistência medida entre esses dois terminais
quando as fontes de alimentação são substituídas pelas suas
resistências internas
A corrente total, Itotal , é dada por:
A corrente através da carga é então, usando a regra da divisão de corrente,
7.29
Etapa 2: Cálculo da resistência equivalente
7.30
Qualquer equivalente de Thévenin pode ser transformado num
equivalente de Norton usando as seguintes relações
VTh
RTh
Para a corrente de Norton:
IN 
Para a tensão de Thévenin:
VTh  RN I N
Circuito equivalente
7.31
7.32
8