Oficina 9

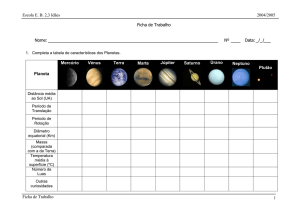
Planetas e exoplanetas
Rosa M. Ros
União Internacional Astronómica
Universidade Politécnica de Catalunha, Espanha
Objetivos
 Compreender o significado dos valores
numéricos das tabelas de dados referentes
aos planetas do Sistema Solar.
 Compreender as principais características
dos sistemas planetários extra-solares.
Sistema Solar
Procuramos modelos
que nos forneçam
outras informações
que não sejam apenas
trabalhos manuais
De acordo com o conteúdo
Procuramos modelos com
conteúdo e que mostrem
alguns aspectos específicos
Maquete para as distâncias ao Sol
Mercúrio
Vénus
Terra
Marte
Júpiter
Saturno
Úrano
Neptuno
57 900 000 km
108 300 000 km
6 cm
11 cm
0,4 AU
0,7 AU
149 700 000 km
228 100 000 km
778 700 000 km
1 430 100 000 km
2 876 500 000 km
4 506 600 000 km
15 cm
23 cm
78 cm
143 cm
288 cm
450 cm
1,0 AU
1,5 AU
5,2 AU
9,6 AU
19,2 AU
30,1 AU
Maquete para os diâmetros
Sol
Mercúrio
Vénus
Terra
Marte
Júpiter
Saturno
Úrano
Neptuno
1 392 000 km
139,0 cm
4 878 km
0,5 cm
12 180 km
12 756 km
6 760 km
142 800 km
120 000 km
50 000 km
45 000 km
1,2 cm
1,3 cm
0,7 cm
14,3 cm
12,0 cm
5,0 cm
4,5 cm
Maquete para os diâmetros
T-shirt com os diâmetros, à
escala, dos planetas.
Diâmetros e distâncias ao Sol
Sol
Mercúrio
1 392 000 km
25,0 cm
4 878 km
57 900 000 km
0,1cm
10 m
Vénus
12 180 km
108 300 000 km
0,2 cm
19 m
Terra
12 756 km
149 700 000 km
0,2 cm
27 m
Marte
6 760 km
228 100 000 km
0,1 cm
41 m
Júpiter
142 800 km
778 700 000 km
2,5 cm 140 m
Saturno
120 000 km
1 430 100 000 km
2,0 cm 250 m
Úrano
50 000 km
2 876 500 000 km
1,0 cm 500 m
Neptuno
45 000 km
4 506 600 000 km
1,0 cm 800 m
Normalmente, nas escolas não existe espaço suficiente
para fazer a construção para além de Marte
Modelo para diâmetros e distâncias
no quintal ...
Modelo na
Cidade
(Barcelona)
Sol
Mercúrio
Vénus
Terra
Marte
Júpiter
Saturno
Úrano
Neptuno
Máquina de lavar louça
Puerta Instituto
ovo de caviar
ervilha
Puerta Hotel Diplomatic
Pasaje Méndez Vigo
ervilha
grão de pimenta
laranja
tangerina
noz
noz
Entre Méndez Vigo y Bruc
Paseo de Gracia
Calle Balmes
Pasaje Valeri Serra
Calle Entenza
Estación de Sants
Modelo na cidade de Metz (França)
Modelo para os tempos
 c = 300 000 km/s
O tempo que a luz demora da Lua à Terra é:
t = distância TL/c = 384 000km/ 300 000 = 1,3 seg.
Como é que seria
uma conversa, entre
os planetas, por
"videoconferência"?
A luz solar demora a chegar ...
Mercúrio
Vénus
Terra
Marte
Júpiter
Saturno
Úrano
Neptuno
57 900 000 km
3,3 minutos
108 300 000 km
149 700 000 km
228 100 000 km
778 700 000 km
1 430 100 000 km
2 876 500 000 km
4 506 600 000 km
6,0 minutos
8,3 minutos
12,7 minutos
43,2 minutos
1,32 horas
2,66 horas
4,16 horas
O Sol visto a partir dos planetas
Terra
 a = tan a = radio Sol/ distância do Sol=
= 700 000/ 150 000 000 = 0,0045 radianos = 0,255º
 A partir da Terra, o Sol mede 2a = 0,51º
O Sol visto a partir dos planetas
de Vénus
da Terra
de Marte
de Mercúrio
de Júpiter de Saturno
de Úrano de Neptuno
Densidades
06/12/03
Mercúrio
5,41 g/cm3
Pirita (5,2)
Vénus
5,25 g/cm3
Pirita (5,2)
Terra
5,52 g/cm3
Pirita (5,2)
Marte
3,90 g/cm3
Blenda (4,0)
Júpiter
1,33 g/cm3
Enxofre (1,1-2,2)
Saturno
0,71 g/cm3
Pinho (0,55)
Úrano
1,30 g/cm3
Enxofre (1,1-2,2)
Neptuno
1,70 g/cm3
Argila (1,8-2,5)
16
Modelo para o achatamento
 Corte tiras de cartolina de dimensões 35 x 1 cm.
 Fixe-as apenas na parte superior de uma vara
de 50 cm de comprimento e 1 cm de diâmetro,
enquanto que na parte inferior devem ser
colocadas de forma a permitir o seu
deslocamento ao longo da mesma.
 Gire a vara, situando-a entre as duas mãos e
fazendo um rápido movimento de rotação num
sentido e noutro. A força centrífuga que
deforma as bandas de cartolina atua também
nos planetas, deformando-os.
Achatamento
Planetas
(raio equatorial-raio polar)/
raio equatorial
Mercúrio
0,0
0,0
0,0034
0,005
0,064
0,108
0,03
0,03
Vénus
Terra
Marte
Júpiter
Saturno
Úrano
Neptuno
Modelo para a velocidade de rotação
 3a lei de Kepler P2/a3 = K permite deduzir que a
velocidade de rotação diminui com o aumento da distância.
Peguemos num cordel em que na
outra extremidade se prendeu uma
anilha e façamo-lo girar sobre a nossa
cabeça
Libertando-se um pouco o cordel, a
velocidade do objeto diminuirá
Removendo-se um pouco o cordel, a
velocidade aumentará
(Conservação da quantidade do
momento).
Modelo para gravidades de superfície
 Gravidade à superfície, F = GMm /d2, com m=1 e d=R.
Então g = GM / R2 , onde M = 4 p R r / 3
 Substituindo, g = 4 p G R r / 3
Gravidade à superfície
Planeta
Raio
Densidade
Equatorial
Gravidade Gravidade
calculada superficie real
Mercúrio
2439 km
5,4 g/cm3
0,378
3,70 m/s2
0,37
Vénus
6052 km
5,3 g/cm3
0,894
8,87 m/s2
0,86
Terra
6378 km
5,5 g/cm3
1,000
9,80 m/s2
1,00
Marte
3397 km
3,9 g/cm3
0,379
3,71 m/s2
0,38
Júpiter
71492 km
1,3 g/cm3
2,540
23,12 m/s2
2,36
Saturno
60268 km
0,7 g/cm3
1,070
8,96 m/s2
0,91
Úrano
25559 km
1,2 g/cm3
0,800
8,69 m/s2
0,88
Neptuno
25269 km
1,7 g/cm3
1,200
11,00 m/s2
1,12
1,62 m/s2
0,16
Lua
Modelo para "crateras de impacto"
 Cobrir o chão com jornais para não o
sujar e depois poder recolher a farinha.
 Coloque, com uma peneira ou coador,
uma camada de 1 ou 2 cm de farinha de
modo que a superfície fique lisa.
 Coloque, com uma peneira ou coador,
uma camada de alguns milímetros de
cacau em pó sobre a farinha.
 De uma altura de cerca de 2 m, deixe
cair uma colher de sopa de cacau em pó
que, ao cair, deixará marcas
semelhantes às crateras de impacto.
 A farinha usada pode ser reciclada para
uma nova simulação.
Velocidade de escape
 Espaço e = ½ a t2 + vo t
 Velocidade v = a t + vo
 Na superfície v0=0, a=g e e =R, então
R = ½ g t2 e v = g t .
Eliminando t, resulta a velocidade de escape
v = (2gR)1/2
Velocidades de escape
Planeta
Mercúrio
Raio
Gravidade
Equatorial superficial
2 439 km
0,378
Velocidade
de escape
4,3 km/s
Vénus
6 052 km
0,894
10,3 km/s
Terra
6 378 km
1,000
11,2 km/s
Marte
3 397 km
0,379
5,0 km/s
Júpiter
71 492 km
2,540
59,5 km/s
Saturno
60 268 km
1,070
35,6 km/s
Úrano
25 559 km
0,800
21,2 km/s
Neptuno
25 269 km
1,200
23,6 km/s
Lançamento de foguetes
 Cartolina
 Embalagem de rolo de
fotografia
 ¼ comprimido
efervescente
Sistemas planetários
extrassolares
1995 Michael Mayor e Didier Queloz
anunciaram a deteção de um
exoplaneta orbitando 51 Pegasi.
1a foto
2M1207b observado diretamente (ESO)
Métodos utilizados para detetar
exoplanetas
São usados ​vários métodos, por exemplo,
 Velocidade radial ou efeito de Doppler
 Método do trânsito
 Microlente gravitacional
 Outros
DESLOCAMENTO
de
DOPPLER
Modelo para sistemas de exoplanetas
São mais de 850 os sistemas de exoplanetas
descobertos e confirmados (e cerca de 3000
exoplanetas a candidatos) (janeiro de 2014).
As massas dos exoplanetas são muitas vezes
comparadas com a massa de Júpiter (1,9 x 1027 kg).
Apenas alguns exoplaneas são de tamanho
semelhante ao da Terra. O motivo deve-se às
limitações tecnológicas.
Nomeação dos exoplanetas
Coloca-se uma letra
minúscula após o nome
da estrela principal,
começando por "b"
para o primeiro planeta
encontrado no sistema
(por exemplo, 51 Pegasi b).
O planeta seguinte é nomeado seguindo a
ordem alfabética c, d, e, f, etc.
(51 Pegasi c, 51 Pegasi d, 51 Pegasi , 51 Pegasi f, …).
Modelo para sistemas exoplanetários
Para visualizá-los, construa-se modelos à escala que nos
permitirá compará-los entre si e com o Sistema Solar.
Nome do
planeta
Distância
Período
Massa Mín. Descoberta Diâmetro
media (u.a) orbital(dias) (Mj ou Mt)
(ano)
aprox. (km)
Ups And b
0,059
4,617
0,69 Mj
1996
124 000
Ups And c
0,83
241,5
1,98 Mj
1999
176 000
Ups And d
2,51
1274,6
3,95 Mj
1999
221 000
GL 581 e
0,030
1,9 Mt
2009
16 000
Gl 581 b
0,041
5,368
15,65 Mt
2005
32 000
Gl 581 c
0,073
12,932
5,36 Mt
2007
22 000
Gl 581 g
0,146
3,1 Mt
2010
18 400
Gl 581 d
0,250
7,1 Mt
2007
250 700
GL 581 f
0.758
7,0 Mt
2010
250 000
83,600
Cálculo de diâmetros de exoplanetas

É comummente assumido que a densidade do
exoplaneta é igual à densidade de Júpiter ou Terra.

Sabendo que a densidade é dada por r = m/V,
sendo m, a massa conhecida, e V, o volume da
esfera, fornecido por V = 4 p R3 /3, então o raio R é
calculado por
3 ________
R = √3 m/(4 p r)
Cálculo da massa da estrela central
 Terceira Lei de Kepler
a / P = const
3
2
com unidades selecionadas
MS = 0,0395×10-18 a3 / P2
onde
Planeta Fomalhaut b (detalhe) em nuvens de
poeira interplanetária
a é o raio da órbita do satélite (em km).
P é o período de rotação do satélite (em dias) e
MS é a massa da estrela central (em massas solares)
Por exemplo, pode-se calcular a massa da estrela central
Ups And e Gl 581 em massas solares (o resultado deve
ser 1,3 e 0,3 massas solares).
Modelo, à escala, de um sistema
exoplanetário
A escala apropriada é:
distância 1 u.a. = 1 m
10 000 km de diâmetro = 0,5 cm.
Neste caso, todos os exoplanetas podem ser
colocados numa sala de aula e os primeiros
cinco planetas do nosso sistema solar
(incluindo Júpiter) podem ser exibidos. Se a
atividade é realizada (por exemplo, no pátio
da escola) poder-se-á construir o modelo
completo.
Podemos construir (sistema solar)
Sistema
Solar
Mercúrio
Vénus
Terra
Marte
Júpiter
Saturno
Úrano
Neptuno
Distância Diâmetro Modelo:
(u.a.)
(km)
distância
0,39
4 879
40 cm
0,72
12 104
70 cm
1
12 756
1m
1,52
6 794
1,5 m
5,2
142 984
5m
9,55
120 536
10 m
19,22
51 118
19 m
30,11
49 528
30 m
Distância 1 u.a. = 1 m
Modelo:
diâmetro
0,2 cm
0,6 cm
0,6 cm
0,3 cm
7 cm
6 cm
2,5 cm
2,5 cm
Diâmetro 10 000 km = 0,5 cm
Podemos construir
(primeiro sistema exoplanetário detetado)
Upsilon
Andromedae
Distância Diâmetro Modelo:
(u.a.)
(km)
distância
Modelo:
diâmetro
Ups And b
0,059
124 000
6 cm
6 cm
Ups And c
0,83
176 000
83 cm
9 cm
Ups And d
2,51
221 000
2,5 m
11 cm
Distância 1 u.a. = 1 m
Diâmetro 10 000 km = 0,5 cm
Podemos construir
(sistema com planetas tipo "terrestres")
Gliese 581
Distância
(u.a.)
Diâmetro Modelo:
(km)
distância
Modelo:
diâmetro
Gl.581 e
0,030
16 000
3 cm
0,8 cm
Gl.581 b
0,041
32 000
4 cm
1,5 cm
Gl.581 c
0,073
22 000
7 cm
1 cm
Gl.581 g
0,146
18 400
15 cm
0,9 cm
Gl.581 d
0,250
250 700
25 cm
12,5 cm
Gl.581 f
0,758
250 000
75 cm
12,5 cm
Distância 1 u.a. = 1 m
Diâmetro 10 000 km = 0,5 cm
Comentários:
 Muitos exoplanetas orbitam mais próximo da sua
estrela principal do que Mercúrio está do Sol,
portanto são muito quentes.
 Muitos dos grandes planetas estão próximos das
suas estrelas porque o método de velocidade radial é
mais sensível para planetas com períodos orbitais
curtos, pelo que faz sentido pensar que a maioria
dos planetas pode possuir órbitas maiores.
Potencial habitabilidade dos exoplanetas
 Na zona habitável do sistema solar há apenas dois
planetas: Vénus e a Terra (mas Vénus é muito
quente por causa do efeito estufa).
(u.a.)
Potencial habitabilidade dos exoplanetas
 Gliese 581 c, poderia conter água líquida e a
possibilidade de vida. No entanto, alguns estudos
indicam que, provavelmente, sofre de efeito de
estufa semelhante ao de Vénus.
 Gliese 581 g, é o primeiro exoplaneta na zona
habitável com gravidade suficiente para manter
uma atmosfera e a temperatura necessárias para
albergar água líquida.

Gliese 581 d, exoplaneta rochoso na zona habitável
de sua estrela-mãe, candidato a acolher vida
extraterrestre.
Conclusões
 Conhecimento mais “preciso" dos planetas.
 Estabelecimento de relações "parâmetros" que
permitem uma melhor compreensão de dimensões.
 O sistema solar "está vazio".
 Introdução aos exoplanetas.
Muito obrigado
pela sua atenção!