Material Utilizado

Exper.
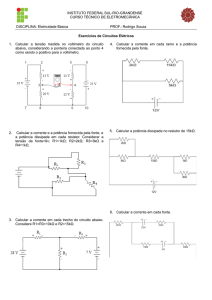
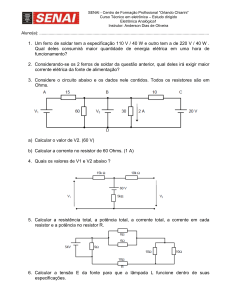
5
Ondas Senoidais e Valor Eficaz
Objetivo
Verificar a relação de valor eficaz com valores instantâneos de sinais alternados
Controle de Operação
Sinais com amplitude variável mas que tenham sempre um mesmo sinal ou sentido são chamados
sinais Corrente Contínua (CC) ou DC (direct current). Observe figura (1).
amplitude
tempo
Figura
Sinal
CC 1
Uma tensão contínua constante tem uma forma de onda representada por uma reta de valor constante.
Sinais alternados tem características de amplitude, freqüência, período e fase. Genericamente, um sinal
do tipo corrente alternada é aquele que adquire valores positivos e negativos durante um período. Observe
figura (2).
amplitude
tempo
Sinal CA
Figura (2)
Figura 2
Amplitude: é o valor de pico do sinal.
Freqüência: é o número de vezes que o sinal se repete, por unidade de tempo.
Período: é o tempo que a onda leva para completar um ciclo.
Fase: indica o deslocamento em relação ao início do eixo do tempo.
As relações entre período e freqüência são dadas por:
f 
1
T
Se o tempo for medido em segundos, a freqüência é dada em Hertz, ou ciclos/segundo.
Valores de tensão lidos em um voltímetro indicam, em geral, o valor eficaz da forma de onda. O valor
eficaz é, teoricamente, o valor de uma tensão contínua que aplicada sobre um resistor dissiparia a mesma
potência que o sinal senoidal em questão. Contudo, o comportamento temporal de sinais alternados é o de
assumir todos os valores dentro de uma determinada faixa de valores. A relação entre valores eficazes e valores
de pico na forma de onda podem ser vistas na figura (1) e é dada por:
1
Vp
Vef 
com
sendo
2
V (t )  V p .sen(t  0 )
Vef : valor da tensão eficaz
Vp : tensão de pico, ou valor máximo de tensão.
Vef
Vp
0
t
V(t)=Vp.sen(t-0)
Figura
Figura(3)3
Para se verificar o valor eficaz de uma forma de onda senoidal, propõe-se a montagem do circuito da Figura 4:
Figura 4
Com a chave 1 fechada e a chave 2 aberta, a potência média dissipada no resistor é:
𝑃 = 𝐸. 𝐼 =
𝐸2
= 𝑅𝐼 2
𝑅
Com a chave 2 fechada e a chave 1 aberta, e considerando a tensão no gerador ac igual a 𝑒(𝑡) =
𝑉𝑝. 𝑐𝑜𝑠(𝑤𝑡 + ∅), a potência média dissipada no resistor é:
𝑉𝑝
2
𝑉𝑝 2 ( ⁄√2)
1 𝑇/2
𝑃𝑎𝑐 = ∫ 𝑒(𝑡). 𝑖𝑎𝑐 (𝑡)𝑑𝑡 =
=
𝑇 −𝑇/2
2𝑅
𝑅
Isto é, a potência dissipada no resistor será a mesma em ambas situações acima se:
𝐸=
𝑉𝑝
√2
2
Material Utilizado
Multímetros.
Varivolt.
Ponte retificadora.
Capacitor.
Resistor (“mergulhão”).
Procedimento Prático
1 – Encha duas vasilhas com o mesmo volume de água e insira um resistor em cada vasilha.
2 – Ligue o varivolt e ajuste a tensão em 220 Vca e ajuste o multímetro para medição de temperatura.
3 – Preencha a Tabela 1, com o valor de temperatura medido, na coluna adequada para cada instante de tempo.
Tempo (s)
Tensão alternada
Tensão contínua
0
30
60
90
120
150
180
210
240
270
300
4 – Insira a ponte retificadora e capacitor para que a tensão a ser conectada no resistor seja contínua. Preencha
a Tabela 1 na coluna adequada para cada instante de tempo.
3