Capítulo 3

Capítulo 3
Formas de ondas
Introdução
A forma de onda de uma grandeza
elétrica é representada pelo respectivo
gráfico em função do tempo.
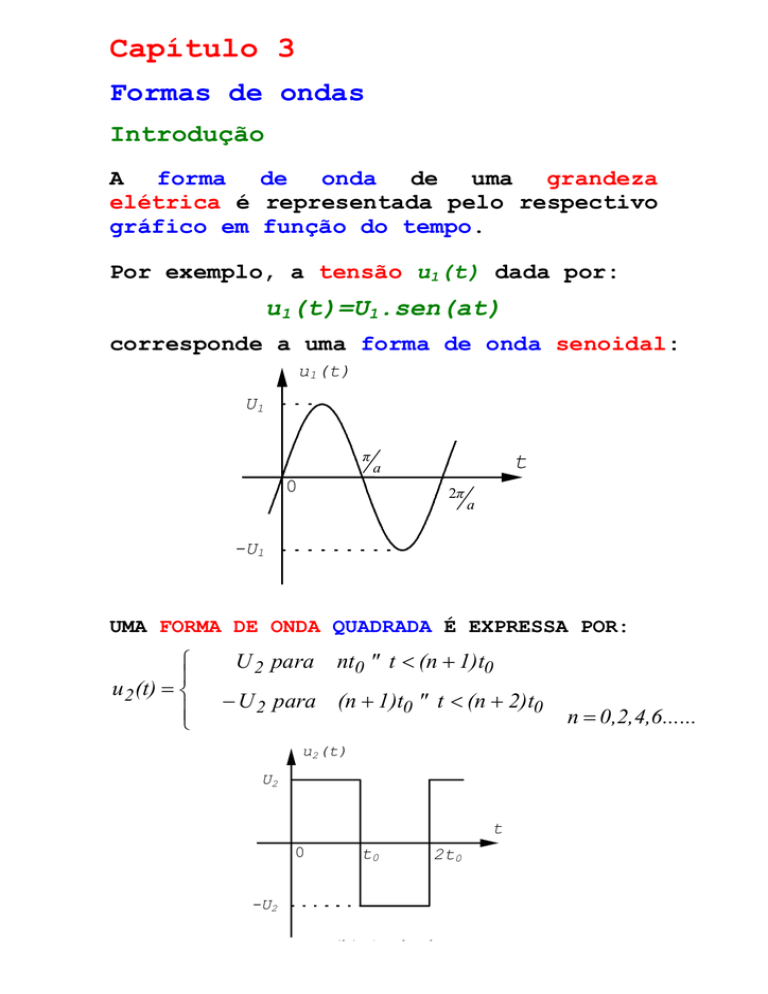
Por exemplo, a tensão u1(t) dada por:
u1(t)=U1.sen(at)
corresponde a uma forma de onda senoidal:
u1(t)
π
Ua
1
π
t
a
0
2π
a
-U1
UMA FORMA DE ONDA QUADRADA É EXPRESSA POR:


u2 (t) = 

U 2 para nt0 ≤ t < (n + 1)t0
− U 2 para (n + 1)t0 ≤ t < (n + 2)t0
u2(t)
U2
t
0
t0
2t0
-U2
(b) Quadrada
n = 0,2,4,6......
CATEGORIAS
de
FORMAS
i(t)
de
ONDAS
i(t)
t
t
t0
t0+T
T
(a) oscilatória
i(t) =
sen(at)
(b) periódica
i(t) = I0 + I1 .sen(at) + I 3 .sen(3at + α)
ebt
Formas
de
ondas
oscilatórias:
são
formas de ondas que crescem e decrescem
alternadamente ao longo do tempo de
acordo com alguma lei definida.
Formas de ondas periódicas: são formas
de ondas oscilatórias cujos valores se
repetem a intervalos de tempo iguais.
i(t)
i(t)
IM
t
t1
t2
∆I
t
t1
t2
-IM
T
(c) alternada
T
(d) periódica
Formas de ondas alternadas: são formas
de
ondas
periódicas
cujos
valores
médios são nulos.
É possível identificar uma forma de
onda
alternada
através
de
uma
interpretação intuitiva de valor médio.
Qual seria essa interpretação intuitiva?
Valores característicos das formas de
ondas periódicas
Ciclo: é o conjunto completo de valores
instantâneos
que
se
repetem
a
intervalos de tempo iguais. Observe
esta figura:
T
i(t)
t1
t2
t
ciclo
T
Período: é o intervalo de tempo T em
que ocorre um ciclo. Veja a indicação
na figura acima.
Freqüência: medida em Hertz (Hz), esta
grandeza corresponde à quantidade de
ciclos por unidade de tempo, sendo
portanto dada por:
f =
T é o período.
1
T
Velocidade angular ou freqüência angular
A figura abaixo mostra a forma de onda
de uma corrente senoidal expressa pela
função:
i(t)=Imax.sen(t)
ou
i(t)=Imax.sen(wt)
i(t)
(a)
Imax
t [s]
T/2
T
0
(a)
-Imax
1 ciclo
i(t)
Imax
0
π
2π
(b)
wt[rad]
-Imax
Tanto faz considerar que o período desta
forma de onda é T segundos ou que o
período desta forma de onda é wt = 2π
π rad.
Comparando os dois gráficos, nota-se que
um mesmo valor instantâneo de corrente
ocorre para o instante de tempo t = T e
para o ângulo wt = wT = 2π
π rad.
Portanto:
2π
= 2.π.f
rad/s
T
A grandeza w corresponde à velocidade (ou freqüência)
angular da corrente i(t).
w=
Exemplo 3.3
No Brasil, a freqüência da tensão senoidal
gerada
nas
usinas
(hidrelétricas
ou
termelétricas) é 60 Hz.
Calcular o período e a velocidade angular.
T=
Período →
1
1
=
= 16,67
f 60
ms
Velocidade angular:
w = 2πf = 2π 60 ≅ 377
rad/s
Valor de Pico: é o valor instantâneo máximo
que a forma de onda atinge no ciclo.
i(t)
Imax
t [s]
T/2
T
0
-Imax
1 ciclo
Valor de Pico:
I p = I max
Ângulo de fase ou simplesmente fase, é
um ângulo arbitrário definido para a
forma de onda de modo a estabelecer um
referencial de tempo para a mesma.
Para estas formas de onda:
i(t) = I p .sen(wt − α)
i(t) = I p .sen(wt + α)
-
i(t)
i(t)
Ip
Ip
-α
0
π-α
wt
2π+α
π+α
-α
α
-Ip
α
0
2π-α
-Ip
Nas duas formas de onda, α corresponde
ao ângulo de fase e no instante t=0 o
valor instantâneo da corrente é:
i(0) = I p .sen( α)
i(0) = I p .sen(-α)
α corresponde ao valor do deslocamento
horizontal
da
onda
em
relação
à
referência “zero”.
wt
Diferença de fase ou defasagem
É a diferença entre os ângulos de fases
de duas formas de ondas.
P2 P1
i2(t)
i1(t)
0
wt [rad]
α
β
ϕ
defasagem
Para
i1(t)=I1.sen(wt+α)
e
i2(t)=I2.sen(wt+β)
a diferença de fase ϕ é dada por:
ϕ = β −α
Por que ϕ é calculado em módulo?
Porque o sinal de ϕ depende da referência.
Na figura qual das formas de onda está adiantada?
P2 P1
i2(t)
0
wt [rad]
α
β
i1(t)
ϕ
defasagem
P2 P1
i2(t)
0
i1(t)
wt [rad]
α
β
ϕ
defasagem
Um método simples de se determinar a
forma de onda que está adiantada ou
atrasada está ilustrado nesta figura.
Identifica-se os picos das formas de onda
mais próximos entre si (ambos positivos
ou negativos) que na figura correspondem
aos pontos P1 e P2. O ponto que se
encontra à esquerda do outro indica que a
respectiva forma de onda está adiantada,
que na figura corresponde ao ponto P2 e
portanto i2(t) está adiantada em relação a
i1(t) ou ainda, i1(t) está atrasada em
relação a i2(t).
Vimos que
ϕ
é calculado em módulo:
E que o sinal de
ϕ
ϕ = β −α
depende da referência.
P2 P1
i2(t)
i1(t)
0
wt [rad]
α
β
ϕ
defasagem
Se i1(t) for a referência, ϕ é positivo.
Se i2(t) for a referência, ϕ é negativo.
ANALISEMOS AS FORMAS de ONDA das
CORRENTES INDICADAS NESTE CIRCUITO:
u(t)
~
R
L
u(t)
iC(t)
iL(t)
iR(t)
C
iC(t)
iR(t)
iL(t)
wt
QUEM ESTÁ ADIANTADA OU ATRASADA?
u(t)
iC(t)
iR(t)
iL(t)
wt
Em relação à tensão na fonte:
A corrente no resistor está em fase
A corrente no indutor está atrasada de 900
A corrente no capacitor está adiantada de 900
Tomando-se como referência de ângulo de
fase, a tensão fornecida pela fonte:
u(t) = Up.sen(wt)
V
iR ( t ) = I R p . sen( wt )
A
i L ( t ) = I Lp . sen( wt − π )
2
iC ( t ) = I C p . sen( wt + π
2
)
A
A
Valor Médio
É definido para uma forma de
periódica u(t) de período T como:
1 t0 +T
U m = .∫
T t0
onda
u (t ).dt
A integral desta equação corresponde à
área total da forma de onda em relação
ao eixo das abscissas no período.
u(t)
A1
to + T
t0
t0+T
2
t
A2
T
Interpretação gráfica do valor médio
Exemplo 3.5
i(t)=7+10.sen(wt+π/6)
A
i(t) (A)
17
0
wt (rad/s)
-3
Notem que é uma forma de onda senoidal
deslocada no eixo vertical de 7 A
O seu valor médio é calculado por:
w
Im =
.
2π
∫
Im
w 
.7
=
2π 

∫
2π
w
2π
0
w
[7 + 10. sen(wt + π 6 ].dt
∫
dt + 10.
0
2π
w
0
(
)
 7.w
sen wt + π dt  =
.t
6 
π
2

2π
w
0
=7 A
Portanto, a corrente i(t) é uma forma
de
onda
periódica,
porém,
não
é
alternada.
Valor Eficaz
Analisemos a potência absorvida por uma
lâmpada que pode ser conectada a uma:
•
fonte c.c. (chave ch1) ou
•
fonte c.a. (chave ch2).
ch1
+
- Ucc
ch2
~
u(t)
lâmpada
Com
ch1
fechada,
circula
corrente
contínua de valor Icc pela lâmpada.
A potência absorvida corresponde a:
2
Pcc = U cc .I cc = ( R.I cc ).I cc = R.I cc
R é a resistência do filamento da lâmpada.
Tomando como referência um instante de
tempo t0, a energia consumida pela
lâmpada em um intervalo de tempo T
vale:
E cc =
∫
t 0 +T
t0
Pcc .dt = R.I cc2 ∫
t 0 +T
t0
dt
E cc = R.I cc2 .T
→
Com ch2 fechada, circula pela lâmpada
uma corrente alternada do tipo:
u (t )
i (t ) =
= I p .sen( wt )
R
Neste caso, a potência absorvida é dada
pelo produto de uma tensão por uma
corrente variáveis no tempo, sendo,
portanto, também variável no tempo:
p(t ) = u (t ).i(t ) = R.i 2 (t )
A energia consumida pela lâmpada em um
intervalo de tempo T a partir de t0 é
dada por:
E ca =
∫
t 0 +T
t0
p(t ).dt
→
∫
E ca = R.
t 0 +T
t0
i 2 (t ).dt
Impondo-se a condição de que a energia
consumida pela lâmpada nos dois casos
seja a mesma, tem-se:
Ecc = Eca
→
R.I cc2 .T
∫
= R.
t 0 +T
t0
i 2 (t ).dt
I cc
1
=
.
T
I cc
1
=
.
T
∫
t 0 +T
t0
∫
t 0 +T
t0
i 2 (t ).dt
i 2 (t ).dt
Sendo T o período da corrente i(t),
1 t0 +T 2
.∫ i (t ).dt corresponde ao valor eficaz
T t0
da corrente alternada i(t):
I ef
1 t 0 +T 2
=
.
i (t ).dt
T t0
∫
CONCLUSÃO:
Se a corrente fornecida por uma fonte
c.c. ( Icc ) for igual ao valor eficaz (Ief)
da corrente alternada i(t), a energia
consumida pela lâmpada é a mesma, tanto
em c.a. como em c.c.
O valor eficaz é também conhecido como
valor rms (root-mean-square).
Exemplo 3.6
Calcular o valor eficaz de u(t) = 179,6.sen (wt)
2π
Sendo o período de u(t) igual a
w
o valor eficaz (Uef) é dado por:
U ef =
U ef =
w 2π w 2
.
u ( t ).dt =
2π ∫ t0
1 2π 2
.
u ( wt ).d ( wt )
2π ∫ 0
(179,6)2 . 2π [sen(wt )]2 .d (wt )
∫0
1 2π
2
.∫ [179,6.sen ( wt )] .d ( wt ) =
2π 0
2π
Aplica-se a relação trigonométrica:
[sen(wt )]2 = 1 .[1 − cos(2wt )]
2
e o valor eficaz de u(t) vale:
(179,6)2 .
U ef =
Uef
 ∫0
4π
=
2π
d ( wt ) − ∫
2π
0
(179,6)2 . wt
cos(2wt ).d ( wt ) =

4π


4π
(179,6)2 .[(2π − 0) − (0 − 0)] = (179,6)2
2
=
2π
0
179,6
2
sen(2 wt )
−
2
≅ 127
V
CONCLUSÃO:
A relação entre o valor de pico e o
valor eficaz, para uma onda alternada
senoidal, é:
Up
U ef
= 2
ou
U ef =
Up
2
2π
0



Visualização de formas de ondas no
osciloscópio
O osciloscópio é o mais versátil
dos instrumentos eletrônicos de
medição, devido à significativa
quantidade de recursos disponíveis
para a análise de formas de ondas.
IMPORTANTE:
Qualquer sinal a ser examinado
em um osciloscópio, deve ser
traduzido em uma tensão.
Exemplo: a forma de onda da corrente
que circula por um motor deve passar
por um resistor linear cuja diferença
de potencial (d.d.p.) será aplicada
ao osciloscópio.
Assim sendo, observamos uma onda
de tensão proporcional à onda de
corrente mas que conserva todas
as características da onda de
corrente.
A QUE CORRESPONDEM
CH1
CH2 e GND?
As indicações CH1 e CH2 referem-se a
dois canais do osciloscópio, e ambos
têm em comum o contato GND (ground)
que é a referência para todas as
medidas em um osciloscópio.
Através de CH1 e CH2 pode-se
observar na tela (display) as
formas de ondas da tensão no
resistor (CH1) e da tensão no
capacitor (CH2).
Note que o GND está conectado
entre os dois bipolos.
Analise:
Se os contatos do GND e do CH2
forem trocados, quais formas de
onda serão observadas na tela do
osciloscópio?
Vídeo:
Conceito de Valor Eficaz
http://www.youtube.com/watch?v=nxpSgrKOrLU