HIGIENE E MEDICINA DO TRABALHO

ANÁLISE DE CIRCUITOS EM
CORRENTE ALTERNADA
Tensão Contínua – Fontes DC
As fontes DC tem polaridades e magnitudes
fixas, e portanto, geram correntes com
valor constante e direção fixa. Exemplo de
geradores que geram tensão continua são
as pilhas e as baterias.
Tensão Alternada
As tensões de fontes AC alternam a polaridade e
variam a magnitude, gerando assim correntes que
variam em magnitude e alternam a direção.
Conforme o comportamento da tensão então
temos os diferentes tipos de tensão alternada:
senoidal, quadrada, triangular, pulsante, etc.
De todas essas a senoidal é a que tem
um
maior interesse pois é a senoidal a tensão que é
gerada nas usinas e que alimenta as industrias e
residências.
Considerando o circuito da figura abaixo, no qual
temos duas baterias e uma chave que ora conecta
a bateria B1 ao resistor, ora conecta a bateria B2 ao
resistor. Vamos supor que cada bateria fica
conectada ao resistor durante 1s. Como seria o
gráfico da tensão em função do tempo nos
terminais da bateria ?
O valor negativo significa que a polaridade da tensão
mudou. Desta forma obtemos uma forma de onda quadrada.
Além desta, usualmente temos aplicações em eletricidade
as formas triangular e principalmente a senoidal.
O tempo que leva para repetir uma mesma situação é 2s,
sendo chamado de período (T). O valor máximo da tensão é
12V ( sendo chamado de valor de pico VP ou valor máximo
VM). A seguir analisaremos mais em detalhes a senoidal.
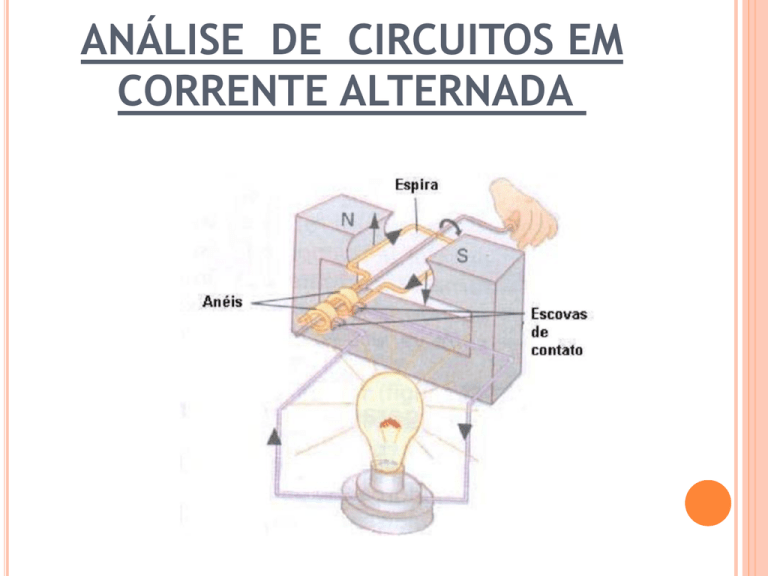
Gerador Elementar de Corrente Alternada
O gerador de corrente alternada é uma aplicação da
indução eletromagnética, convertendo energia mecânica
em energia elétrica.
Um
gerador
de
corrente
alternada
é
constituído
basicamente de uma espira (ou um conjunto de espiras)
girando numa região onde existe um campo magnético.
Enquanto a espira gira, há uma variação do fluxo magnético
através dela. Isto ocorre porque a inclinação da espira, em
relação ao campo magnético, está variando continuamente.
Gerador Elementar de Corrente Alternada
Então uma força eletromotriz é induzida na espira,
gerando uma corrente induzida. Durante uma meia-volta da
espira, o fluxo magnético através dela aumenta e, ao
efetuar a meia-volta seguinte, o fluxo diminui. Em outras
palavras, a espira girando dentro de um campo magnético
gera uma corrente alternada, coma se pode perceber pela
indicação do amperímetro. Lei de Faraday e = .l.vt
e = tensão induzida no condutor
 = indução em Tesla (T)
l = comprimento do condutor sujeito ao campo
vt = velocidade com que o condutor corta o campo
transversalmente
e = .l.vt
e = .l.v.sen 
e = Emáx.sen 
Tensão Senoidal
É uma tensão que varia com o tempo de acordo com uma
lei senoidal, portanto nesse caso temos uma expressão
matemática para expressar a tensão (no caso da tensão
quadrada não temos). A expressão matemática é:
v(t)= VP.sen(wt + o)
ou
v()
= VP.sen 
Onde VP (em V) é o valor de pico (valor máximo que a
tensão pode ter), w em (rd/s) é a freqüência angular e 0
(rd ou graus) é o angulo de fase inicial,  é o ângulo num
determinado instante t.
Observe que a relação entre ângulo e tempo é dada por :
 = 0 +w.t
Tensão Senoidal
A freqüência angular relaciona-se com a freqüência,
expressa em ciclos por segundo ou Hertz (Hz), através
de:
=2f
A freqüência pode ser expressa em função do período,
através de:
f= 1/T
Todos estes parâmetros da senóide estão graficamente
representados na figura seguinte
Representação Gráfica
VPP (em V) é chamado de tensão de pico a
pico, T (em s) é o período da função.
VPP (em V) é chamado de tensão de pico a pico, T
(em s) é o período da função.
Então uma tensão senoidal varia em função do
tempo de acordo com uma lei senoidal, mas a
mesma tensão pode ser representada em função
do ângulo (não esqueça que a função seno tem
período de 360 graus ou de 2 rd), sendo a relação
entre ângulo e tempo dada por = 0 +w.t
Representação gráfica de uma tensão senoidal
em função do ângulo
A rotação da bobina ao longo de 360º geométricos
(1 rotação ) gera sempre 1 ciclo (360º) de Tensão
(Gerador de 2 pólos).
Corrente Alternada
Quando uma tensão senoidal é ligada aos terminais de uma
resistência de carga, a corrente também é uma onda senoidal.
EXEMPLO
Ω
FREQUENCIA E PERÍODO
O número de ciclos por segundos é chamado de
Freqüência.
É representada pela letra f e unidade em Hertz [Hz].
O intervalo de tempo para que um ciclo se complete é
chamado de período.
É representado por T e expresso em segundos [s].
A freqüência é o inverso do período, ou seja:

Quanto maior a freqüência, menor o período.
Exemplo
Uma corrente CA varia ao longo de um ciclo
completo em 1/100s. Qual o período e a freqüência?
Se a corrente tiver um valor máximo de 5A, mostre
a forma de onda para a corrente em graus e em
segundos.
Graficamente
Relações
de Fase
Para a tensão
senoidal
representada abaixo
•Odetermine
ângulo de fase
entre parâmetros:
duas formas deV onda
de mesma
os seus
P=VM= ______V,
freqüência
é a diferença
instante.
VPP= _____V,
VRMS= angular
____V,num
T= dado
____ms,
f= ____Hz,
•Na figura abaixo, o ângulo de fase entre as ondas B e A é
w = ____ rd/s e 0 = ____
de 90º.
•Enquanto a onda B começa com seu valor máximo e cai
para zero em 90º.
•A onda B atinge o seu valor máximo 90º na frente de A.
•Este ângulo de fase de 90º entre as ondas B e A é mantido
durante o ciclo completo e todos os ciclos sucessivos.
Representar as seguintes tensões senoidais
v1(t) = 15.sen(2. .103.t ) ( V ).
v2(t) = 20.sen(2. .103.t + /2 )( V ).
FASORES
•Forma alternativa para representação de correntes e
tensões alternadas (senoidais).
•Um fasor é uma entidade com módulo e sentido.
•O comprimento do fasor representa o módulo da
tensão/corrente alternada.
•O ângulo em relação ao eixo horizontal indica ao
ângulo de fase.
REPRESENTAÇÃO FASORIAL
•Tomando com exemplo a figura abaixo, o fasor VA
representa a onda de tensão A com ângulo de fase de
0º.
•O fasor VB é vertical para mostrar o ângulo de fase de
90º com relação ao fasor VA, que serve de referência.
REPRESENTAÇÃO FASORIAL
•Quando duas ondas estão em fase, o ângulo de fase é
zero. As amplitudes se somam.
•Quando as ondas estão exatamente fora de fase, o
ângulo de fase é de 180º. Suas amplitudes são opostas.
EXEMPLO
Qual o ângulo de fase entre as ondas A e B? Faça o
diagrama de fasores primeiro com a onda A como referência
e depois como a onda B como referência.
•Ângulo de fase é a distância angular entre pontos
correspondentes nas ondas A e B.
•Os pontos correspondentes mais convenientes são os
pontos de máximo, dos mínimos e dos zeros de cada onda.
•No cruzamento dos zeros no eixo horizontal, =30º.
Valores Características de
Tensão e de Corrente
•Valor de pico é o valor máximo VMax ou IMax.
•Valor de pico a pico é igual ao dobro do valor de pico, quando os picos
positivo e negativo são simétricos.
•Valor médio, corresponde à média aritmética de todos os valores numa
onda senoidal, considerando um meio ciclo.Valor Medio = 0,637x valor
de pico
•O valor rms de uma onda senoidal corresponde à mesma quantidade
de tensão ou corrente contínua capaz de produzir a mesma potência
dissipada.
•O valor eficaz ou rms ou valor médio quadrático corresponde a 0,707
vezes o valor de pico. Valor rms = 0,707x valor de pico
Valores Características de
Tensão e de Corrente
Exercício
Calcule o ângulo de fase para as seguintes ondas CA e
desenhe os respectivos diagramas de fasores
Circuitos Resistivos em CA
Em circuitos CA somente com resistência:
oTensão e Corrente estão em fase;
oEsta relação entre V e I em fase, significa que este circuito
CA pode ser analisado pelos métodos usados para o circuito
CC. Seja o circuito, abaixo, em série.
Indutância, Reatância
e
Circuitos Indutivos
Indutor
Chamamos de indutor a um fio enrolado em forma de
hélice em cima de um núcleo que pode ser de ar ou de
outro material. A figura abaixo mostra o símbolo para
indutor com núcleo de ar, de ferro e de ferrite.
Indutor em Corrente Contínua
O que acontece quando no circuito da figura abaixo quando
fechamos a chave? A tensão é aplicada no indutor mas a corrente
leva um certo tempo para crescer, a explicação é um fenômeno
chamado auto indução. Ao abrir a chave, no instante t2, novamente
esse fenômeno vai atuar na bobina não deixando a corrente se anular
instantaneamente.
A capacidade de um condutor possui de induzir tensão em si
mesmo quando a corrente varia é chamada de auto-indutância ou
simplesmente indutância.
Indutância Mútua
Quando a corrente num condutor ou numa bobina varia, este
fluxo pode interceptar qualquer outro condutor ou bobina nas
vizinhanças, induzindo tensões em ambos.
Características das Bobinas
A indutância de uma bobina depende de como ela é enrolada,
material do núcleo em torno do qual é enrolada, e do número de
espiras que formam o enrolamento.
„A indutância L aumenta com o número de espiras N em torno do
núcleo. A indutância aumenta com o quadrado do número de
espiras.
„ A indutância aumenta com a permeabilidade relativa r do
material de que é feito o núcleo.
„À medida que a área A abrangida em cada espira aumenta. A
indutância aumenta com o quadrado do diâmetro.
„A indutância diminui à medida que o comprimento da bobina
aumenta.
Indutor em Corrente Alternada Senoidal
A corrente em um indutor está atrasada em relação à
tensão em um circuito CC. O que acontece se
alimentarmos um indutor ideal de indutância L com
uma tensão alternada senoidal de freqüência f?
A corrente continua atrasada em relação à tensão e
agora de um ângulo bem definido, 90º.
Conclusão
Um indutor se opõe à passagem de uma corrente alternada
(se opõe à variação de uma corrente) e que a corrente
está atrasada em relação à tensão.
Caso o núcleo fosse de ferro ou ferrite a corrente
demoraria mais para aumenta (ou diminuir),
isto
porque a indutância da bobina seria diferente em cada
caso. A indutância (L) de um indutor é um parâmetro que
dá a medida da capacidade que tem o indutor de
armazenar energia no campo magnético, a sua unidade se
chama Henry (H).
Reatância Indutiva
Como vimos um indutor se opõe à variação de
uma corrente. A medida desta oposição é dada
pela sua reatância indutiva ( XL ), sendo calculada
por:
Com L especificado em Henrys
hertz (Hz), XL em ohms (  ).
(H),
f
em
Capacitância,
Reatância
Capacitiva e Circuitos
Capacitivos
Capacitor em corrente alternada senoidal
Quando ligamos um capacitor em um circuito CC,
inicialmente a corrente é máxima com tensão nula no
capacitor, isto é, existe uma defasagem entre a corrente e
a tensão. Se um capacitor ideal (não tem resistência de
perdas) for ligado à uma tensão alternada senoidal, a
corrente estará 90º adiantada em relação à tensão.
Um capacitor é um dispositivo elétrico formado por
duas placas condutoras de metal separadas por um
material isolante chamado dielétrico.
CAPACITÂNCIA
Capacidade de armazenamento de carga elétrica no dielétrico.
Quantidade de carga que pode ser armazenada num capacitor
dividida pela tensão aplicada às placas. Onde
C=capacitância,F
Q= quantidade de carga,C
V=tensão,V
Capacitor em Corrente Contínua
A tensão no capacitor não pode variar instantaneamente fazendo
queinicialmente funcione como um curto circuito (I=E/R e Vc=0).
Depois de um certo tempo (t=RC) o capacitor passa a funcionar
como um circuito aberto (Vc=E e I=0).
Capacitor em corrente alternada senoidal
Quando ligamos um capacitor em um circuito CC,
inicialmente a corrente é máxima com tensão nula no
capacitor, isto é, existe uma defasagem entre a corrente e
a tensão. Se um capacitor ideal (não tem resistência de
perdas) for ligado à uma tensão alternada senoidal, a
corrente estará 90º adiantada em relação à tensão.
Reatância Capacitiva
É a medida da oposição oferecida pelo capacitor à
passagem da corrente alternada é calculada por:
com C em Farads (F), f em Hertz (Hz) resultando
XC em Ohms ().
Para calcularmos o módulo da corrente no circuito
poderemos usar a lei de Ohm, isto é :
IMPEDÂNCIA COMPLEXA
Define-se impedância complexa, Z a razão entre os
vetores girantes da tensão e da corrente:
Explicitando a impedância complexa de cada um
dos elementos R, L e C, obtém-se:
Uma impedância complexa expressa-se em Ohm 
IMPEDÂNCIA COMPLEXA
Pode-se representar vetorialmente as impedâncias e as
amplitudes complexas de cada um dos elementos.
Note-se que a impedância não é um vetor girante, pois
não está a representar qualquer grandeza alternada
senoidal.
Saliente-se, também, o fato de as impedâncias das
indutâncias e dos capacitores se alterar com a freqüência
de alimentação do circuito, contrariamente ao que
acontece com a impedância da resistência
CIRCUITO RL SÉRIE
Na prática um indutor apresenta uma resistência, e além disso
podemos ter resistores em série com o indutor, neste caso a corrente
continuará atrasada em relação à tensão mas de um angulo menor
do que 90º. A figura mostra o circuito e o diagrama fasorial, com as
seguintes expressões:
Impedância RL série
A resultante da adição dos fasores R e XL é chamada de
impedância. É representada pelo símbolo Z. A impedância é
a reação total ao fluxo da corrente em ohms [Ω].
circuito RL série
Exemplo: Um circuito CA com RL em série tem uma corrente de
1A de pico, com R=50 Ω e XL=50 Ω. Calcule VR, VL, VT e . Faça
o diagrama de fasores de VT e I. Faça também o diagrama de
tempo i, vR, vL e vT.
circuito RL série
Exercício: Para o circuito pede-se determinar:
a) Impedância, b) corrente, tensão em R e em L, c) cos
e d) Formas de onda da tensão total e da corrente
CIRCUITO RC SÉRIE
Relembrando, em um circuito puramente resistivo a
tensão e a corrente estão em fase, e num circuito
puramente capacitivo a corrente esta 90º adiantada em
relação à tensão. Num circuito como o da figura abaixo a
corrente continua na frente da tensão mas de um angulo
menor do que 90º. Observe o seu diagrama fasorial
resultante.
circuito RC série
Define-se a impedância (Z) do circuito como sendo: Z=V/ I
A impedância é a soma dos efeitos da resistência (R=VR/ I) e da
reatância capacitiva (XC=VC/ I) na oposição à passagem da corrente.
O diagrama fasorial nos mostra o seguinte:
1-  é o angulo de defasagem entre a tensão total
e a corrente consumida pelo circuito (I).
2- A corrente no capacitor continua adiantada
em relação à tensão no capacitor (VC).
3- A corrente na resistência (I) está em fase com a tensão na
resistência(VR) e defasada de 90º em relação à tensão no capacitor(VC).
A tensão total do circuito é obtida somando VR com VC vetorialmente.
Do diagrama fasorial obtemos as relações básicas deste circuito:
circuito RC série
Se dividirmos por I2 a primeira igualdade obteremos
expressão que calcula a impedância do circuito
a
O angulo de defasagem, ,também pode ser calculado a partir do
diagrama fasorial sendo dado por:
cos = R / Z
logo
= arcos(R/Z)
CIRCUITO RLC SÉRIE - RESSONÂNCIA
Para analisar o circuito abaixo deveremos lembrar que a
tensão total aplicada é a soma vetorial das tensões VC, VR e
VL. No diagrama fasorial a tensão na resistência está em
fase com a corrente, a tensão na indutância está adiantada
de 90º enquanto a tensão no capacitor está atrasada de 90º
circuito rlc série - ressonância
No diagrama fasorial estamos considerando, arbitrariamente,
que o circuito é indutivo, e portanto VL > VC, e desta forma
a corrente estará atrasada em relação à tensão. Para obter a
expressão da tensão total e da impedância devemos fazer a
soma vetorial das três tensões.
Observe que VL e VC tem mesma direção mas sentidos
oposto, logo a resultante da operação VL - VC terá o sentido
de VL.
circuito rlc série - ressonância
Impedância e Ressonância
Para o circuito anterior vale as seguintes expressões:
Da equação que se obtém o calculo da impedância
observamos que se XL= XC a impedância será igual a R, isto
é, o circuito será puramente resistivo e a corrente estará em
fase com a tensão. Esta situação é conhecida como
ressonância, e ocorre numa freqüência f0 calculada por :
circuito rlc série - ressonância
O circuito ressonante tem as seguintes características:
•Na freqüência de ressonância, o circuito é puramente resistivo, sendo
a corrente máxima de valor V/R, estando em fase com a tensão.
•Abaixo da freqüência de ressonância a impedância será capacitiva
(XC > XL), estando a corrente adiantada em relação à tensão.
•Acima da freqüência de ressonância a impedância será indutiva (XC
< XL), estando a corrente atrasada em relação à tensão.
CIRCUITO RC PARALELO
As mesmas considerações feita para o circuito RC série vale
para o RC paralelo, ou seja, em um circuito puramente
resistivo a tensão e a corrente estão em fase, e num
circuito puramente capacitivo
a corrente
esta 90º
adiantada em relação à tensão.
circuito RC paralelo
Para este circuito valem as expressões
CIRCUITO RL PARALELO
No circuito abaixo temos o circuito e o diagrama fasorial
de um circuito RL paralelo. A corrente total se divide
entre o indutor e o resistor e continuam válidas as
características do indutor ideal (corrente atrasada de 90º
em relação à tensão).
circuito RL paralelo
É importante notar que a fase inicial da tensão do gerador é
ARBITRÁRIA.Caso tivéssemos considerado a fase inicial de V igual
a 0º, todo desenho deveria ser deslocado de 90º no sentido horário.
Cálculo da Impedância
Do ponto de vista de análise, não interessa
saber qual a fase inicial da tensão da rede. O
que importa realmente é a defasagem entre a
tensão total (tensão da rede) e a corrente total
(corrente fornecida pela rede), e o que
determinará essa defasagem será a carga (R e
L). Para este circuito valem as seguintes
expressões.
Z= R.XL/(R2+XL2)0.5
circuito RL paralelo
Exemplo
CIRCUITO RLC PARALELO - RESSONÂNCIA
Como sabemos, num circuito paralelo a tensão é a mesma
em todos os elementos, veja o circuito RLC paralelo e o
diagrama fasorial com a representação das três correntes e
da tensão total.
circuito rlc paralelo - ressonância
Considerando que IL >IC então obtemos o diagrama fasorial
final onde representamos a soma vetorial das três
correntes(IL, IC e IR).
circuito rlc paralelo - ressonância
Para este circuito são válidas as expressões :
Ressonância
Se XL = XC na expressão da impedância obteremos Z = R,
isto é, o circuito será puramente resistivo sendo esta situação
chamada de ressonância e isso ocorre na freqüência f0 dada
por:
O circuito ressonante tem as seguintes características :
•Na freqüência de ressonância f0, o circuito é puramente
resistivo, sendo a corrente mínima de valor V/R, estando em fase
com a tensão.
•Abaixo da freqüência de ressonância a impedância será indutiva
(XC < XL ), estando a corrente atrasada em relação à tensão.
•Acima da freqüência de ressonância a impedância será capacitiva
( XC > XL ), estando a corrente adiantada em relação à tensão.
FILTROS
FILTROS: são circuitos que deixam passar só sinais de
determinadas frequências, atenuando as outras.
De acordo com as frequências que devam passar, pode-se ter os
seguintes tipos de filtros:
a) Filtros Passa Alta (F.P.A)
b) Filtros Passa Baixa (F.P.B)
FILTROS
c) Filtros Passa Faixa (F.P.F)
d) Filtros Rejeita Faixa (F.R.F)
fcs = frequência de corte superior
fci = frequência de corte inferior
As frequências de corte, são frequências nas quais a corrente cai
para um valor igual a 70,7 % da corrente máxima.
FILTROS
As frequências de corte, são frequências nas quais a corrente cai
para um valor igual a 70,7 % da corrente máxima.
Na prática, é impossível se obter um filtro que apresente uma
mudança tão brusca no ganho, o que existe é uma mudança com
uma determinada atenuação com a frequência.
FILTROS
FILTROS
Filtro Passa Alta
FILTROS
Filtro Passa Alta
FILTROS
Filtro Passa Alta
Conclusão: acima da frequência de corte não há atenuação do
sinal de entrada (vi). Abaixo da frequência de corte, o sinal de
entrada é atenuado 10 vezes toda vez que a frequência
diminui 10 vezes.
FILTROS
FILTROS
FILTROS
Filtro Passa Baixa
Os gráficos a seguir, representam a curva real e a
aproximação por trechos de retas.
REFERÊNCIAS
http://www.lei.ucl.ac.be/multimedia/eLEE/PO/realisations/Cir
cuitsElectriques/index.htm
http://www.dt.fee.unicamp.br/~www/ea513/ea513.html