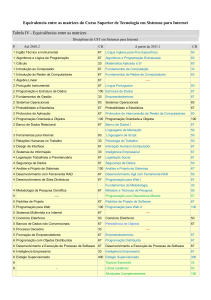
MAT 22119 – 1a prova - Turma F
1ª Questão (2 pontos) Uma amostra de chapas de aço produzidas por uma máquina
forneceu as seguintes espessuras (em mm): 6,34 6,38 6,40 6,30 6,36 6,36 6,38 6,20
6,42 6,38
(a) Forme a tabela de distribuição de frequências por ponto
x
f
6,20
1
x f
6,30
1
63,52
6,34 6,36
1
2
x
2
6,38 6,40 6,42
3
1
1
Total
10
f 403,5144
(b) Calcule média, mediana e moda.
X
63,52
6,36 6,38
6,352 ;Mediana =
6,37 ;Moda = 36,8
10
2
(c) Calcule variância, desvio padrão e coeficiente de variação
403,5144 10 6,352 2
S
0,003928 ; S 0,0626 ; CV 0,9855%
10 1
2
2ª Questão (3 pontos) Um certo índice econômico foi aplicado a uma amostra de
empresas. Os resultados foram:
classes
f
F
1,00 |---- 1,07
1,07 |---- 1,14
1,14 |---- 1,21
1,21 |---- 1,28
1,28 |---- 1,35
1,35 |---- 1,42
Total
Calcule:
14
22
16
13
7
3
75
14
36
52
65
72
75
-------
x
1,035
1,105
1,175
1,245
1,315
1,385
--------
(a) percentagem de valores menores que 1,21
x f
x2 f
87,145
101,9593
(16+22+14/75 = 69,33%
(b) percentagem de valores maiores ou iguais a 1,28
(c) média, mediana e moda
13,33%
37,5 36
Mediana 1,14 0,07
1,1466
16
16
Moda 1,07 0,07
1,107
16 14
X
87,145
1,1619
75
(d) desvio padrão e coeficiente de variação
S
87,145 2
75 0,0974
75 1
101,9593
CV 8,386%
3ª Questão (3 pontos) Uma urna contém 3 bolas brancas, 5 vermelhas e
Extraindo-se, sem reposição 3 bolas, calcule a probabilidade:
11 10 9
0,4533
(a) nenhuma seja branca
14 13 12
(b) exatamente uma seja vermelha 3
6
pretas.
5 9 8
0,4945
14 13 12
(c) todas da mesma cor
3 2 1 5 4 3 6 5 4
0,08516
14 13 12 14 13 12 14 13 12
(d) uma de cada cor
6
3 5 6
0,2473
14 13 12
4ª Questão (2 pontos) Em uma cidade em que os carros são testados para emissão de
poluentes, 25% deles emitem quantidade considerada excessiva. O teste falha para 99% dos
carros que emitem excesso de poluentes, mas resulta positivo para 17% dos carros que não
emitem quantidade excessiva. Qual a probabilidade de que um carro com resultado
A = emite poluentes em quantidade excessiva
+ = resultado positivo no teste
P(A)=0,25; P(Ac)=0,75
- = resultado negativo no teste
P( - | A)= 0,99;
P( - | Ac)= 0,17
(a) negativo no teste realmente emitir quantidade excessiva de poluentes?
P A |
P( A) P( | A)
0,2845
P( A) P( | A) P( A c ) P( | A c )
(b) positivo no teste realmente não emitir quantidade excessiva de poluentes?
P A c |
P( A c ) P( | A c )
0,9807
P( A c ) P( | A c ) P( A) P( | A)