FIS01183 – Turma C/CC – Prova 4 Resolvida - if

FIS01183 – Turma C/CC – Prova 4 Resolvida
Questão 1 – Num recipiente, uma camada de água (n = 1,33) de 20 mm de espessura flutua sobre outra
camada de tetracloreto de carbono (n = 1,46) de 40 mm de espessura. Quando olhamos sob incidência normal
para uma moeda no fundo do recipiente, a que distância abaixo da superfície da água parece estar essa
moeda? Essa distância é chamada de distância aparente. O que acontece quando fechamos um olho?
_______________________________________________________________________________________
Resposta:
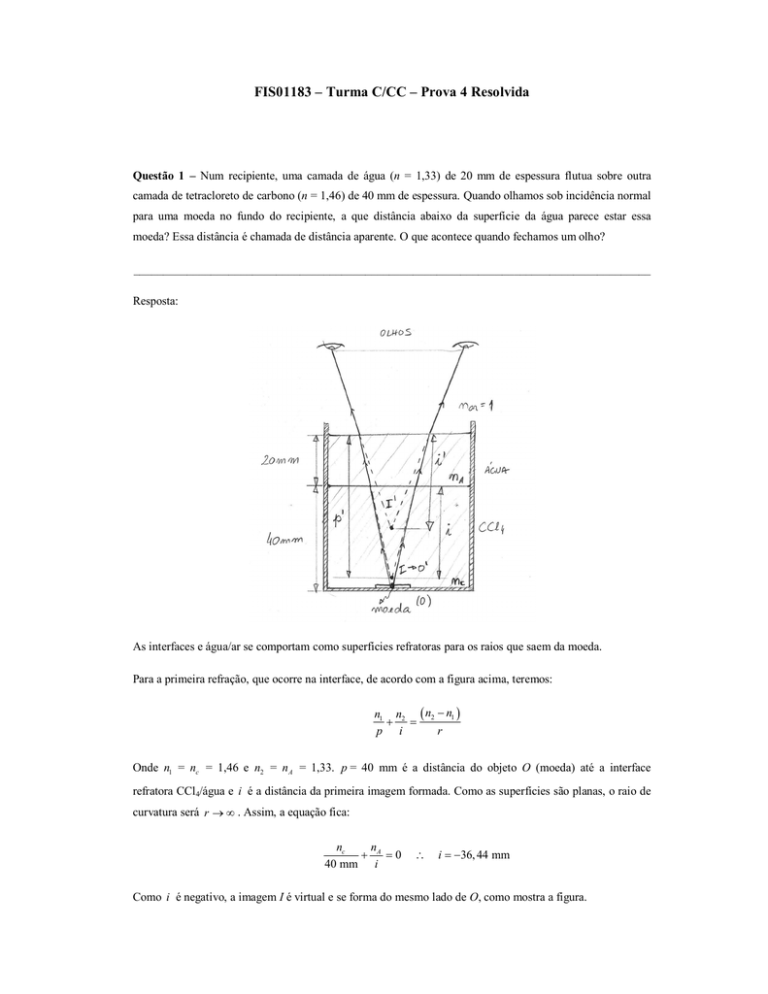
As interfaces e água/ar se comportam como superfícies refratoras para os raios que saem da moeda.
Para a primeira refração, que ocorre na interface, de acordo com a figura acima, teremos:
n1 n2  n2  n1 
 
p i
r
Onde n1 = nc = 1,46 e n2 = n A = 1,33. p = 40 mm é a distância do objeto O (moeda) até a interface
refratora CCl4/água e i é a distância da primeira imagem formada. Como as superfícies são planas, o raio de
curvatura será r   . Assim, a equação fica:
nc
n
 A 0
40 mm i

i  36, 44 mm
Como i é negativo, a imagem I é virtual e se forma do mesmo lado de O, como mostra a figura.
Para a segunda refração, através da interface água/ar, a imagem virtual I formada na primeira refração será o
objeto real O’, cuja distância à segunda superfície será p '  i  20 mm  56, 44 mm (ver figura). Além
disso, agora n1 será nA = 1,33 e n2 = nar = 1. A equação fica:
nA
n
 ar  0
56, 44 mm i '

i '  42, 44 mm
i ' é negativo, pois I’ é virtual, e representa a distância aparente da moeda quando olhamos com incidência
normal. Portanto, a moeda parece estar mais próxima, a 42,44 mm da superfície da água.
Se fecharmos um dos olhos, a moeda parecerá estar deslocada horizontalmente, e perderemos a noção de
profundidade.
_______________________________________________________________________________________
Questão 2 – Uma fibra óptica consiste em um núcleo de vidro (índice de refração n1) envolvido por uma
película (índice de refração n2 < n 1). Suponha um feixe de luz que vai do ar para a fibra fazendo um ângulo
 com o eixo da fibra, conforme mostra a figura.
(a) (1,5 pontos) Encontre uma expressão para o maior ângulo possível de  , para o qual um raio pode
propagar-se pela fibra, e que seja função apenas de n1 e n2.
(b) (1,0 ponto) Calcule o valor de θ, sabendo que os índices de refração do vidro e da película são 1,58 e
1,53, respectivamente.
n2
n1
_______________________________________________________________________________________
Resposta:
(a) Na entrada do raio na fibra, ocorre uma refração, que pode ser descrita pela Lei de Snell (com nar = 1):
1sen   n1 sen 1
Para que a onda continue na fibra, o ângulo de incidência com a normal à superfície núcleo/capa deve ser
maior ou igual a  c (condição de RIT):
sen  c 
n2
n1
Agora, vamos relacionar  c com 1 . O triângulo abc marcado na figura nos dá  c 

 1 .
2
n
sen 


Logo, sen  c  sen   1   cos 1  2 . Mas cos 1  1  sen 2 1 e, da Lei de Snell, sen 1 
.
n1
n1
2

Substituindo essa relação na primeira e após arranjos algébricos para isolar  , temos:
  arcsen
(b)   arcsen

n12  n2 2

 1, 58  1,53   0, 4 rad  23, 2
2
2
_______________________________________________________________________________________
Questão 3 – Um objeto está colocado na frente de uma lente convergente, a uma distância igual ao dobro da
distância focal f1 = +10 cm da lente. No outro lado da lente está um espelho côncavo, de distância focal f2 = 5
cm, afastado da lente por uma distância 2(f1 + f2). Determine a localização, o tamanho relativo e a natureza
(direita ou invertida, real ou virtual) da imagem final, vista por um observador olhando para o espelho
através da lente.
_______________________________________________________________________________________
Resposta:
O observador está colocado à esquerda da lente (ver figura).
1. Lente convergente. p = 20 cm, f1 = +10 cm
1 1 1
 
p i f1
Temos também, que m  

1
1
1
 
20 cm i 10 cm
 i  20 cm
i
20 cm

 1 , ou seja, a imagem I do objeto original O formada pela lente
p
20 cm
convergente está a 20 cm à direita da lente, é real, invertida e tem o mesmo comprimento de O.
2. Espelho côncavo. Agora a imagem I formada pela lente será o objeto real O’ para o espelho. Assim, p ' =
10 cm (em relação a espelho), pois a distância entre a lente e o espelho é de 30 cm, obtida de 2  f1  f2  , e
f2 = 5 cm.
1 1 1
 
p ' i ' f2
E também, m '  

1
1
1
 
10 cm i ' 5 cm
 i '  10 cm
i'
10 cm

 1 , ou seja, a imagem I’ gerada pelo espelho do objeto O’ será invertida
p'
10 cm
em relação a este (mas direita em relação ao objeto original O), estará 10 cm à esquerda do espelho (portanto,
a 20 cm à direita da lente) e é real.
3. Lente convergente. Para que o observador veja a imagem através da lente (do seu lado), se formará uma
imagem I’’ pela lente convergente. Agora, I’ será o objeto real O’’ para a lente. p '' = 20 cm.
1 1 1
 
p '' i '' f1
E m ''  

1
1
1
 
20 cm i '' +10 cm
 i ''  20 cm
i ''
20 cm

 1 , ou seja, a imagem I’’, do lado do observador, estará a 20 cm à esquerda da
p ''
20 cm
lente (mesma posição do objeto original O), será invertida, real, e terá o mesmo comprimento.
A ampliação lateral total deste conjunto será dada por M  m  m ' m ''  1 . A imagem final I’’ será invertida,
mesmo tamanho que O, real, e estará na mesma posição (ver figura).
_______________________________________________________________________________________
Questão 4 – Um objeto é colocado a uma distância de 60 cm à esquerda de uma lente divergente com
distância focal de -15 cm. A uma distância de 10 cm à direita desta lente está outra lente, convergente, com
distância focal de +20 cm.
(a) (1,0 ponto) Determine a localização da imagem final formada pelo sistema.
(b) (1,5 ponto) Qual a ampliação transversal total do sistema? Diga se a imagem final é real ou virtual, direita
ou invertida.
_______________________________________________________________________________________
Resposta:
(a) Lente divergente. p = 60 cm, f1 = -15 cm.
1 1 1
 
p i f1

1
1
1
 
60 cm i 15 cm
m
 i  12 cm
i
12 cm

 0, 2
p
60 cm
A imagem I formada pela lente divergente do objeto O está a 12 cm à esquerda desta lente, é virtual, menor e
direita (ver figura).
Lente convergente. Agora, a imagem I formada pela lente divergente será o objeto real O’ para a lente
convergente. p '  i  10 cm  22 cm e f 2 = +20 cm.
1 1 1
 
p ' i ' f2

1
1
1
 
22 cm i ' 20 cm
m'  
 i '  220 cm
i'
220 cm

 10
p'
22 cm
A imagem I’ estará a 220 cm à direita da segunda lente, será real e aumentada em relação a O’ em 10x e
invertida.
(b) Ampliação lateral total: M  m  m '  0, 2  (10)  2 . A imagem final será real, invertida e com o
dobro da altura de O.