Caderno de Exercícios 4

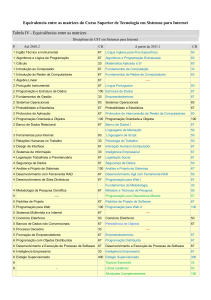
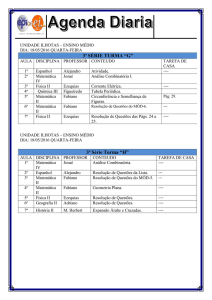
Departamento de Economia,
Gestão e Engenharia Industrial
Universidade de Aveiro
Introdução à Economia
2º semestre
Ano Lectivo 2010/2011
Caderno de Apoio Nº. 4
Teoria do Produtor
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 2/9
“O custo de produção não teria qualquer efeito sobre o preço de concorrência se
não pudesse ter nenhum efeito sobre a oferta”.
John Stuart Mill
In Samuelson & Nordhaus (2005), “Microeconomia”, pág. 147.
4.1. Defina de forma sucinta e rigorosa:
a) Função de produção.
b) Produto total, Produtividade Média e Produtividade Marginal.
c) Isoquanta e isocusto.
d) Taxa marginal de substituição técnica.
e) Custo fixo, custo variável e custo total.
f) Custo marginal e Custos Médios.
g) Lucro do Produtor.
h) Rendimentos crescentes, constantes e decrescentes à escala.
i) Rendimentos decrescentes à escala versus rendimentos marginais decrescentes.
j) Economias de Escala e Economia de Gama.
4.2. “A função de produção supõe já resolvidos os problemas de eficiência na utilização dos factores
produtivos”. Será esta afirmação verdadeira? Justifique devidamente a sua resposta.
4.3. Comente as seguintes afirmações:
a) Um dado produtor de milho e trigo verificou que após um bom ano agrícola o seu rendimento tinha
diminuído.
b) “As associações de produtores de azeite, perante o aumento do preço do azeite, prevêem uma
diminuição das suas receitas totais”.
4.4. Diga se concorda ou não com as seguintes afirmações e justifique a sua resposta:
a) “Uma combinação produtiva economicamente ineficiente será também tecnologicamente ineficiente”.
b) “Uma combinação produtiva tecnologicamente ineficiente será também economicamente ineficiente”.
4.5. Com a ajuda dos gráficos seguintes, analise a substituibilidade entre os factores de produção X1 e X2.
X2
X2
X2
Fig. 1
X1
Fig. 2
X1
Fig. 3
X1
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 3/9
4.6. Suponha a produção de um determinado bem, o qual envolve a utilização de trabalho, capital e terra,
cujos preços são iguais. Será que isto implica a utilização da mesma quantidade de qualquer dos factores
produtivos?
4.7. Distinga as figuras a) e b) quanto ao horizonte temporal e justifique as suas respostas.
Figura a)
Figura b)
4.8. Suponha que uma determinada fábrica se depara com vários processos alternativos de produção de um
determinado produto. Esses processos diferenciam-se pela diferente intensidade de emprego dos dois
factores de produção mais importantes neste caso: trabalho e capital.
Interrogado acerca das quantidades destes dois factores necessários para se produzir três quantidades
alternativas do output em causa, um técnico forneceu o seguinte quadro:
Níveis de Output
Diferentes
Técnicas possíveis
A
B
C
D
E
F
G
H
I
L
K
3
2
3
4
5
6
7
8
14
10
6
4.5
3.5
3
2.7
3
II
L
4
3
4
5
6
7
8
9
K
14
11
8
6.3
5
4.4
4
4.4
III
L
5.5
5
5.5
6
7
8
9
10
K
15
12
9
8.3
7
6
5.6
6
a) Faça uma representação gráfica das isoquantas apresentadas.
b) Pressupondo que o preço do capital é 1 u.m. e que o preço do trabalho é 2 u.m. e que o gestor pode
dispor, no máximo, de 16 u.m., trace a recta de isocusto e determine, justificando, a combinação
óptima de factores de produção.
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 4/9
4.9. Suponha que o Sr. Bonifácio explora uma propriedade com uma área de cerca de cinco hectares, onde
tradicionalmente cultiva searas de trigo. O Sr. Bonifácio sabe, por experiência de largos anos, que a
relação existente entre o número de trabalhadores empregues na produção de trigo e a quantidade
produzida deste cereal é a que consta do seguinte quadro: (exercício dado na parte da aula teórica)
PRODUÇÃO DE TRIGO (área de 5 ha)
Número de trabalhadores (L)
1
2
3
4
5
6
7
8
Produção total (alqueires) (Q)
10
24
39
52
61
64
65
64
a) Elabore um quadro, e represente graficamente, os valores do produto marginal, produto médio e
produto total.
b) Imagine agora que o Sr. Bonifácio paga 10 000 € de renda anual ao dono da terra, na qual se situa a
sua exploração agrícola e que, em média, tem de pagar anualmente a cada trabalhador a quantia de
7 000 €.
Elabore um quadro onde figurem os custos fixos, os custos variáveis e os custos totais
experimentados.
c) Elabore um quadro onde figurem os custos fixos médios, custos variáveis médios e os custos totais
médios, tentando relacionar o andamento destes três tipos de custos. (Se julgar necessário, elabore um
gráfico).
d) Porque razão o mínimo da curva de custos totais médios é atingida a uma produção mais elevada que
o mínimo da curva de custos variáveis médios?
4.10. Admita que a sua equação de custos é do tipo
CT = f (Q) + b
Calcule as expressões das curvas de: CF, CV, CFM, CVM, CTM e CMg.
4.11. Qual o efeito dos seguintes acontecimentos sobre os custos fixos, variáveis, totais e sobre o custo
marginal quando:
a) O Estado lança um imposto de 5 000 euros sobre todas as empresas produtoras de cimento para
financiar programas anti-poluição.
b) Um novo contrato laboral é assinado com o sindicato que representa os trabalhadores da empresa,
consagrando um aumento de 10% nos salários.
c) O Estado lança um imposto de 5 cêntimos por cada unidade vendida.
d) Um aumento da contribuição para a segurança social leva a empresa a pagar mais 10 euros, por mês,
por cada trabalhador empregue.
e) Ocorre um aumento em 2% da renda de parte das instalações fabris da empresa.
f) Ocorre um aumento do consumo de energia eléctrica.
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 5/9
4.12. No ano de 1999, uma pequena empresa do sector têxtil apurou os seguintes dados relativos aos seus
custos e receitas:
Quantidade produzida
Receita Total
Custo Total
(103 metros de tecido
(103 escudos)
(103 escudos)
1
2
3
4
5
6
7
1500
2900
4100
5100
6000
6600
7000
700
1400
2200
3100
4200
5500
7000
a) Represente num diagrama apropriado as curvas de receita total e de custo total.
b) Calcule as receitas marginais e os custos marginais desta empresa. Represente ambos num mesmo
diagrama.
c) Calcule os custos totais médios desta empresa, e represente-os num outro diagrama juntamente com os
custos marginais.
d) Determine a quantidade de tecido óptima a produzir e a vender, por esta empresa, isto é, a quantidade
que maximiza o lucro da empresa.
e) Represente esta quantidade óptima nos gráficos das alíneas a) e b).
4.13. Imagine uma empresa com a seguinte curva de custos totais:
CT =
Q3
− 7Q 2 + 111Q + 50
3
a) Esta curva de custos será de curto ou de longo prazo? Justifique.
b) Quais as funções representativas dos Cmg, CF, CV, CFmédios, CVmédios e CTmédios?
4.14. Considere o gráfico seguinte, o qual representa o andamento dos custos de uma empresa:
C
B
15
5
A
0
20
Q
a) Identifique as curvas A, B e C.
b) Determine o total dos custos fixos no ponto Q = 20.
c) Indique um possível valor do custo marginal para o nível de produção Q = 20 e justifique a sua
resposta.
d) Determine o total das despesas variáveis para uma produção igual a 20 unidades.
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 6/9
4.15. Diga se concorda ou não com a seguinte afirmação de um director comercial de uma empresa
portuguesa, e justifique a sua resposta:
“ O custo médio de produção da empresa onde trabalho representa aquilo que custa produzir cada
unidade de produto. Como o preço de venda deste produto representa aquilo que a empresa ganha por
unidade vendida, o nível de produção que maximiza o lucro da empresa é aquele para o qual o preço
iguala o custo médio de produção”.
4.16. “No curto prazo, a curva de custo marginal de uma empresa (operando em mercado de concorrência
perfeita) pode ser vista como a curva de oferta dessa empresa, mas apenas a partir do ponto em que o
custo marginal é superior ao custo variável médio”. Explique.
4.17. Admita que a produção de um determinado bem se processa de acordo com a seguinte função de
0, 5
0,5
produção do tipo Cobb-Douglas: Q = L K . Onde Q representa o nível de produção, L o número de
unidades de trabalho e K o número de unidades de capital incorporados no processo produtivo.
O produtor dispõe de 100 u.m e os preços dos factores de produção são inicialmente P L =10 e P K =10.
a) Qual o tipo de rendimentos à escala que a função de produção exibe? Justifique.
b) Qual a combinação óptima de factores de produção? E o nível de produção alcançado?
c) Suponha que o capital passa a ser subsidiado e o seu preço reduz-se a metade do preço inicial. Qual é a
nova combinação óptima de factores de produção e respectivo nível de produção alcançado?
4.18. A Pescavelha é uma empresa que possui uma frota pesqueira própria e que processa industrialmente o
seu pescado vendendo o seu produto final a diversos supermercados.
Suponha que a sua unidade industrial de processamento tem uma função de produção dada por
Q = 4L 0 , 4 K 0, 6 . O preço do trabalho é actualmente de €20 por unidade e do capital é de €30 por unidade.
a) Explique o que é uma isoquanta e uma isocusto.
b) Represente as linhas de isocusto associadas aos seguintes níveis de custo: C1=10000, C2=12500 e
C3=15000.
c) Sabendo que a empresa em questão pretende produzir um nível de produção dado por Q = 1000
unidades, que combinação de trabalho e capital próprio deverá esta empresa utilizar para minimizar
o custo total de produção associado?
4.19. Sendo Q = AL α K β , quais os valores que α e β devem tomar para que esta função apresente:
a) Rendimentos crescentes à escala;
b) Rendimentos constantes à escala.
c) Rendimentos decrescentes à escala.
4.20. Uma empresa apresenta inicialmente uma produção total de 1000 unidades que aumenta para 2200
unidades. Comparativamente, o factor produtivo capital passa de 100 u.m. para 200 u.m.
a) Calcule o produto marginal e o produto médio.
b) Neste caso, como caracteriza os rendimentos à escala?
b1) E se a produção apenas tivesse aumentado apenas para 2000 unidades?
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
(
4.21. Uma pequena empresa apresenta a seguinte função de produção Q = min K 0.5 , 2 L0 ,5
corresponde o seguinte mapa de isoquantas:
pág. 7/9
)
a que
K
K=2L
a) Qual a expressão da via de expansão da produção?
b) Qual a utilização óptima dos factores para produzir 10 unidades de Q? E para produzir 12 unidades?
c) Qual a taxa marginal de substituição entre factores, em qualquer um destes pontos óptimos (ver
gráfico acima)?
d) Sabendo que a empresa tem custos fixos de 500 u.m. e que os preços dos factores (seus únicos custos
variáveis) são P K = 1 e P L = 6, qual o custo de produzir 10 unidades de Q?
e) Deduza a função de custos totais.
2
f) Admitindo que a função de custos totais é dada por: CT = 500 + 4Q , e o preço de mercado do seu
produto é P = 40, qual o nível óptimo de produção?
g) Qual a curva de oferta desta empresa?
h) Admitindo que neste sector existem 80 empresas todas iguais, qual a expressão da sua curva de
oferta agregada?
4.22. (adaptado de 1º Teste de Av. Mista, 2010) A empresa TEST1 utiliza dois factores produtivos: capital
(K) e trabalho (L) segundo uma dada tecnologia representada por Q(K,L) = K*L. Esta empresa possui um
orçamento de 160 u.m. para despesas com esses factores produtivos. O preço do factor produtivo trabalho
é 2 u.m. e o preço do factor produtivo capital é 4 u.m.
a) Determine o tipo de rendimentos à escala da função de produção desta empresa. Justifique e
caracterize.
b) Qual a combinação óptima de factores produtivos e a quantidade máxima que é possível obter a partir
do orçamento disponível? Represente graficamente.
c) Determine a expressão analítica da via da expansão da produção e explique o seu significado.
d) Esta empresa está produzir no curto ou no longo prazo? Justifique.
4.23. Comente as seguintes afirmações:
a) “Dados os preços dos factores produtivos, produtividade média decrescente implica custos variáveis
médios crescentes”.
b) “Uma empresa com lucro contabilístico nulo terá lucro económico negativo”
c)
“Uma combinação produtiva economicamente ineficiente será também tecnologicamente
ineficiente”.
d) “Atendendo à lei dos rendimentos marginais decrescentes podemos explicar o porquê da curva de
custos marginais ter um segmento decrescente e um segmento crescente”.
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 8/9
4.24. Diga se são verdadeiras ou falsas as seguintes afirmações:
a) Ganhos de produtividade são conseguidos, obtendo-se o mesmo volume de produção, com um
aumento significativo do número de trabalhadores empregados.
b) Um aumento na oferta conduzirá a uma redução no preço de equilíbrio e a um aumento na
quantidade de equilíbrio.
c) Para a determinação da curva da oferta, o progresso tecnológico é irrelevante.
d) A taxa marginal de substituição técnica é decrescente ao longo da curva de indiferença.
e) A diminuição da produtividade e da competitividade leva obrigatoriamente ao encerramento de
empresas e a uma diminuição da oferta.
f) O excedente do produtor é a diferença entre o preço de venda e o custo de produção dos bens.
g) Quanto mais inclinada for a curva da oferta, tanto mais elástica será a oferta.
h) As elasticidades da procura e da oferta são sempre positivas.
i) Os custos fixos são constantes para qualquer nível de produção da empresa/produtor.
j) Os custos totais são zero quando a empresa não produz nada.
k) A taxa marginal de substituição técnica é constante ao longo de uma isoquanta.
l) Se a produção aumentar de 1000 para 1300 unidades resultante de um aumento do factor produtivo
trabalho de 50 efectivos para 75 efectivos, então estamos perante uma situação de rendimentos
constantes à escala.
m) Uma empresa que no ponto de maximização do lucro tem Q=200, P=10; CVM= 8; CTM=12 e
CFM= 4 deverá encerrar no curto prazo.
4.25. Seleccione a alínea correcta:
4.25.1 A taxa a que uma empresa pode substituir um factor produtivo por outro, mantendo o nível de
produção constante, é conhecido por:
a) Grau de economias de escala;
b) Taxa marginal de substituição;
c) Taxa marginal de substituição técnica;
d) Produto marginal.
4.25.2. Para a produção de sapatos são necessárias combinações de capital (K) e trabalho (L) segundo a
seguinte função: Q = KL. Sabe-se ainda que a taxa marginal de substituição técnica é dada por:
TMST = K/L, e a função custo total é dada por: CT = L + 2K. Se o nível de produção for igual a 50, o
montante de custo total correspondente é:
a) 10;
b) 5;
c) 25;
d) 20.
Introdução à Economia – 2º semestre
Ano Lectivo 2010/2011
Cap.4
pág. 9/9
4.25.3. Considere que no gráfico seguinte a área dada pelo triângulo ABE corresponde ao:
a)
b)
c)
d)
Excedente do consumidor;
Excedente do produtor;
Excedente económico;
Nenhuma das anteriores.
4.25.4. Se uma empresa não encerrar então deve produzir a um nível de produção em que:
a) A receita média iguale o custo médio;
b) O preço seja igual ao custo marginal;
c) A receita marginal iguale o custo médio;
d) O custo total iguale a receita média.
4.25.5. A função produção de bolachas integrais é descrita como Q = L0,5Kβ. Sabendo que a função exibe
rendimentos decrescentes à escala, o valor de β pode ser:
a) 0,5;
b) 0,2;
c) 0,7;
d) 1.
4.25.6. O excedente do produtor é tanto maior quanto:
a) Menor for o preço do bem;
b) Maior for o declive da curva da oferta;
c) Maior for o preço do bem;
d) Nenhuma das anteriores.
4.25.7. A PmgL é:
a) O número adicional de unidades de produto que resultam da utilização de mais um aunidade de
trabalho;
b) O número adicional de unidades de trabalho necessárias para produzir uma unidade adicional do
produto;
c) O número adicional de unidades de produto que têm de ser recrutadas para produzir o actual
volume de produção;
d) Nenhuma das anteriores
E:,~er<.IGGj
ae E..~\Q
Y.
QcdeRm
o)
~
l.
1
c,-s .c,
.,
.a
G
lÇ
~I
1.!
13
1"
,<;
~ç,
S)
_í'r,
1-
(?L -~
R:::!cG
8
3
GS
ct..'-2._
1L.L_-Xl.<á....
.p toO:(\ <J
\....
lo~\
---'::l
_
Ç.
q
r
~
"'-
.f, '-t
8
.1
-i
-~
"'4
.~<"
----Lu::
~c/c:.1\
c: c\"\
'c>
(uS!cl'
~\,
r
:1 \
,IC!()..
_Q,:iL __ O~.D..33
_ 1__
.
-
l:L11-
_
Gd
_,\-1-__~.'l'l-
Idr-oi
m
--
(ç./c:nl-
'"
------_1-
o,.ifL
L
!?<.!~\c)'.
'tl'!(\S.ro (e{rol
--.Lc\J I t::l \ \
I
~
Í"-~~'O.Oj<,(C\)
..ip.Y.
..o,.:::,~Q,
F'
o
_
--4---·---
_
/
.....
--- -----~
--0--
---
-----
-D-~Ic':>~S
-
Slk~C1niCWe\
---
__
~~s...:Jo.Q\O'~
ri) Q,
-----
r------.e \
,-:.o
eú ----.ld~---.OO
\/oa.iá
_~e-
\.tncckd.eL >Le:ac:lld..os.1
~i .~~',~~~Q.~~~~~--
rUS:K:L'~
!;l)M~~'
-
--~-
-- --
---
-----
-~~~-=-------
~o.0,"J,
-
'C..3-~,
íG.._::5O"-
_
-~
c.... ___
----
-LI)
---
ç::~\e e\tc)"IC
li---
-
~)-
e' de-
----
-----
Ov-.:->t'l
:::
r,
--
1\(:::,
U
---
~
--
--
----------
-----
_
____
-
-~
~l=~<::.ç:....\':L_u::..J ~----
._-----
~
--
~~~~~@
(?~-~~
(
--
,<~!'\<
a:o.asi~"
Gl_
--
------
--
---
-----------t1"LL
_
~~_\_-----
----t---
-
\2..\1 ~
:;,
1.-
JX- - 'J, Q_"U
---~-
-
---=---
------
1--_~s:D
--
--
1
-
----j
~----
-
-----
-------
L-fL--1.t -
-----------
--
- - -~~"----~=::- -------Q
-----
- -
--
-------
-
--~---_.
------"
----~
AoLo~o,-;
------=---\<.eC'lc\' cne.1t"O
--------
---'-------
----
o:~
G oL
'f o,,>
• :-\
r
lo')
PL',\O
T
c3~
P
"'
J:L
~_l
l"-l
I
+,
LO'"
I{.,
::.
'6..°"
1 lO,l.
Ç)V,
",S
.2.L.
( =-.1
r
/0,5-1-
,-oS.L ~_
l..c.s
es
,
I
aS
p
I
~..J:.k
o,~-1
f'fe
I
I
l
l --
,--o$"
I,
".
,~---
IJ..
o,'
l
J
0"5'
(~l,
_0,'5
\' ,
p.r;
• '"
J
o,,
--
r
\~.L
Iho,s
0\')
1-
0\')
!to
v:. -:
L
r
l
\
r
--r
,
r
--
~ PL~ 10
L
M,~O
_
\.-
r'
í'
Y:,:5
x:
'"
_
'01-
c,S
S
e: o,>
,.)
.r
o,s-
~
Q:;
1'- ~ \6
~
!
r
(.l(,-::
$:',
oS
o,'?
h.
-~
l: L
:;~
\
v,')
y,::..x..L-
,o5~
1:.1
oS
GA..:... . 'h
.~
+«
,-;'("('lC;f...._
Ph
V
I
í
r
O,S
,\~'J,', f
-",
XL
~- 1
1.
\
'-
~o.o
\
_YL.L1(1
\\.
~
~
(CI "1C1C\ (',\
1 --
"':"',5-
=-.
..L-
,,-oL
G
----
----~ ~
___
S
o,ç
-1.Q---
._-
..1-8_-:
__
_
o.~
lli
Lt-l~
0,<;;
ri ~.LO
---___
oS
_
_
-----
-.-f"(,~3.0
-ij-
------
~)
------+-~-
--
---
--------
-----
_
--------------
----ij--------
----
-
-----------
---------f\.-
___
-ij-
~;~Q~,~f>L~~nU,C~iL_
_
-~-----__
-
f.,,~ 1QCCG
-
-----..::,~
.?,1,..~
-----
-----
------
------
---
--------:;--------
-
- --
---;-----
-----------------t----.6
!~.::<O'~-Gj~.~
~OOQ
~-\'-I - -~j
--_-----li-
o
-
~
"
j
mc.1i
.J
k~~G~:l__
o
-----.e:t
t..
0;,.," '
&....-~'L _-L __
P
qli
...J.. _,
0,0<;1,
06 ..
py
t~
I
-----ll---__li-~-::LQ------'----
---
---
---
-
-,,.--------'7---
----!'---j------
f---
I
l -(
- ---
-----7---- --
-----------
----
-- ---
._--
--___
\..
-
-
-r---.-- ------
\-
--->-(~:-l'___ll------
- -------
--r"--1..,.,.:' _-_
-
~
r---
-r--.(
~ l -;.i $"0
----
-----
---------:,---- --
---
"
c,)
~o,G
_
l::Lu..-
DL '>I±(3.=
]°30
bJ
,.
'-i~2...Q:>IT'O
-km
<><+j3 J::!.- 5iJnih(O ~e
-
Oé:r,ó·rneút'.0 cnesa:nlR 'o
llm
r-
r
U
'
r~~
í lJ rY'c,jf,
,,~
L~L " ~A..
~
P'(L
r-
r-
I
L:)
-es(Q\.Q
1(-,
L
.L
rL
P."'-
L~l
Á·
'\
L:c
~
,
- -L
{)
-'-
N.
1..:\
, -L
t
(
o~
'-I
..)
lo.-
--'.
(),
L=2
r
-("
(
~ 2L
~
----'--
v-"~-º-.~i..-
~
-;
I
\=
~'
....L:
--L
Gi',t::_ ) o
2D'K-I.J..Q::
1<',\
i
--c
"
I
O
@
- __
+-~-l--_
__ _ __
__
_
_
_
_
__________
2
;-LiISL_ --
_
--- ----- ~"----
_
------------~
':2..
-
-
------!
-
----
--
---
------
----
-----------------+-----1
--11-----------
------
--
___
--------
_ __
------'ê..-
_
-----H-~.zs----___
':i.25 __~C\...j_'__________
_ __
_
---
____
c.. -
2 S .
Lj
11-
OU'...11
_
-------
-----
---
"['1SI..::...'flL--
"
_ _ ___
---
--
.(3-<;0
<3.."0
_~
_-jf
__
---
-
_
----------
-------
_
---
----
----"-------
_
---
-
--..;----
---7--
---
-----
-----------I..I'
c~
o
.b i:_~_0..r:uc;-L
_
-_.0-
r
í~--------
---+--,f--! ...;P:..lÚ..l."'''+'8rl~:o.~--'--(z,)L-\----"6.~ =.~
(
---- --
-.......hl.
~l
(--
L
lL--~-
p"c",-'1___
-11-_
---
Q:::_iL· ~
--~--------- ~
-----7(--------
(
1 « ~ LlL-- __ ~_ ...::5~.
____
Il-__ ----'i'--lh---L =- ío
_
----------
(e: ) ,.;
.--LL\ _=__ 5:D_1.. _L L--=-.iDo..
,
____ --"---'
.-:r_o- ~
,,-"-"
\"
,~
...I..-..;-~....L'-L-
--="'.LU.
_
2.
---11----
----
-----
-- ---
-
---- ----------'-
--
----
"-----~----~Il__---~)
--
-------------------------
----
---
-"-------
_.....::.._------
------
---
----
'::L25.5-
S '\
':L J.S.G-""",--~)
.s
/
1)1Ll.~
u"i 6..c.d.es
0°
cdiC:CcO-
de...un~~.~:.lil..:u\.\±C-·
<:;
fWIII,t<lOl
00-- \.t";.J~QC;.é:ó
d~JnaG
d~ ~oSG..thQ.
I~I'
~)