Exercícios

setor 1214
12140409
12140409-SP
Aula 26
DINÂMICA DO MCU
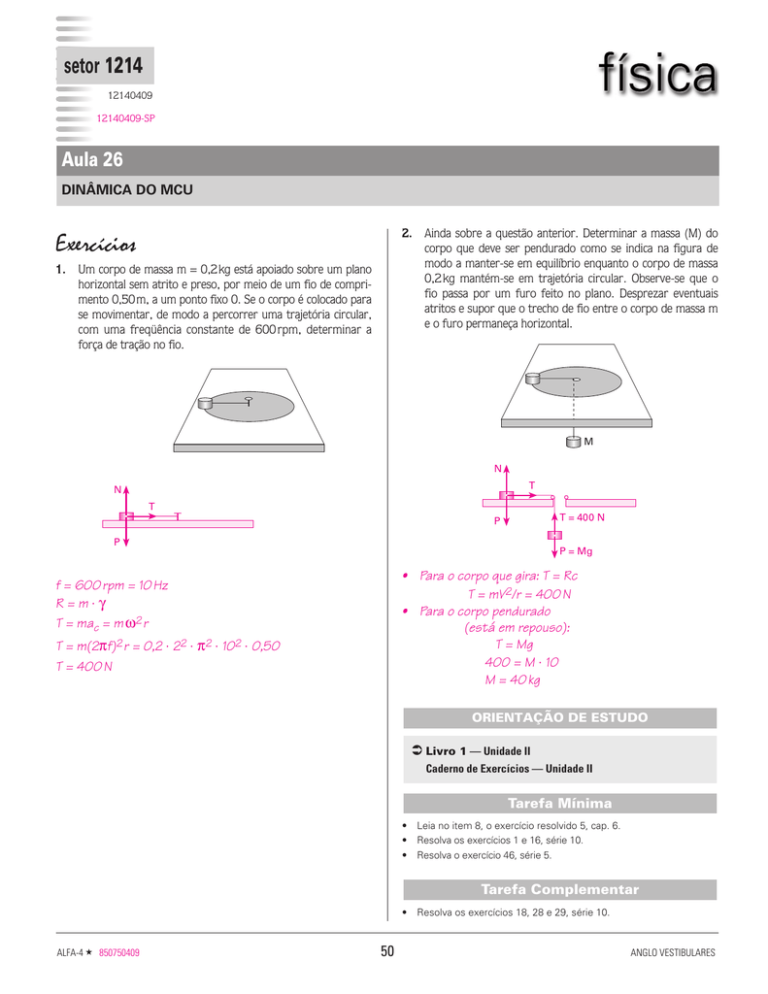
2. Ainda sobre a questão anterior. Determinar a massa (M) do
corpo que deve ser pendurado como se indica na figura de
modo a manter-se em equilíbrio enquanto o corpo de massa
0,2kg mantém-se em trajetória circular. Observe-se que o
fio passa por um furo feito no plano. Desprezar eventuais
atritos e supor que o trecho de fio entre o corpo de massa m
e o furo permaneça horizontal.
Exercícios
1. Um corpo de massa m = 0,2kg está apoiado sobre um plano
horizontal sem atrito e preso, por meio de um fio de comprimento 0,50m, a um ponto fixo 0. Se o corpo é colocado para
se movimentar, de modo a percorrer uma trajetória circular,
com uma freqüência constante de 600 rpm, determinar a
força de tração no fio.
M
N
T
N
T
T = 400 N
P
P
P = Mg
• Para o corpo que gira: T = Rc
T = mV2/r = 400 N
• Para o corpo pendurado
(está em repouso):
T = Mg
400 = M ⋅ 10
M = 40 kg
f = 600 rpm = 10 Hz
R=m⋅γ
T = mac = m ω2 r
T = m(2πf)2 r = 0,2 ⋅ 22 ⋅ π2 ⋅ 102 ⋅ 0,50
T = 400 N
ORIENTAÇÃO DE ESTUDO
Livro 1 — Unidade II
Caderno de Exercícios — Unidade II
Tarefa Mínima
•
•
•
Leia no item 8, o exercício resolvido 5, cap. 6.
Resolva os exercícios 1 e 16, série 10.
Resolva o exercício 46, série 5.
Tarefa Complementar
•
ALFA-4 ★ 850750409
50
Resolva os exercícios 18, 28 e 29, série 10.
ANGLO VESTIBULARES
Aulas 27 e 28
PÊNDULO CÔNICO E PISTA INCLINADA
2. Um pêndulo de massa 2kg efetua um movimento circular e
uniforme em torno do centro C, suspenso por um fio ideal de
comprimento 2m. Sendo a aceleração da gravidade igual a
10m/s2 e o ângulo que o fio forma com a vertical igual α
(sen α = 0,6; cos α = 0,8) determine:
a) O raio da curva descrita.
b) A intensidade da força de tração.
c) A intensidade da resultante.
d) A velocidade escalar do corpo.
Exercícios
1. Uma esfera presa por um fio a um ponto fixo (O) percorre
uma trajetória circular, horizontal (pêndulo cônico). A esfera
fica sob ação de 2 forças (desprezando-se a resistência
a tração e o peso
. A aceleração da
do ar) que são
centrípeta
. A resultante das forças tem
esfera é
direção horizontal e é dirigida para o centro da curva
(Ponto C ).
O
α
α
C
a) sen α = r/ (Δ1) ⇒ r = sen α = 1,2 m
b) cos α = P/T (Δ2) ⇒ T = P/cos α = 25 N
c) tg α = R/P (Δ2)
R = Ptg α = 20 ⋅ (0,6/0,8) = 15 N
d) R = m ⋅ V2/r ⇒ V = 3,0 m/s
T
MCU
P = mg
P
R
aC
T
R = mV2/r = mω2r
α
h = cos α
1
α
P
T
2
R
r = sen α
ALFA-4 ★ 850750409
51
ANGLO VESTIBULARES
3. Um carro percorre uma pista com a forma de um tronco de
cone com raio r e inclinação constante θ em relação à horizontal. O motorista declara que existe uma certa velocidade V
que permite que o carro faça a curva sem que ele, motorista,
vire a direção.
a) Se você não acredita que isso seja possível, escreva:
o motorista mentiu.
b) Se você acredita que isso seja possível, determine V em
função de r, g e θ.
c) Supondo que o carro, percorrendo a pista com a velocidade calculada no item anterior, passasse por uma mancha
de óleo na pista, podemos garantir que:
i) o carro escorregaria para fora da curva;
ii) o carro escorregaria para dentro da curva;
iii) o carro não escorregaria nem para fora nem para dentro
da curva.
r
N
R
P
θ
N
θ
ORIENTAÇÃO DE ESTUDO
P
Livro 1 — Unidade II
Caderno de Exercícios — Unidade II
R
a) Para saber se isso é possível ou não, vamos determinar a
velocidade na qual o carro faria a curva sem a colaboração do atrito. Se existir essa velocidade, o motorista
não mentiu.
Tarefa Mínima
AULA 27
•
b) tg θ = R/P
tg θ = mac/mg
tg θ = ac/g
tg θ = V2/rg
Resolva os exercícios 2 e 3, série 10.
AULA 28
•
Resolva os exercícios 9 e 10, série 10.
V = 公僓僓僓
r ⋅ g僓僓僓僓僓僓
⋅ tg θ
Tarefa Complementar
AULA 28
c) iii) O carro não escorregaria. A mancha de óleo eliminaria o atrito que já não estava agindo.
ALFA-4 ★ 850750409
•
•
•
52
Resolva os exercícios 4 e 5, série 10.
Resolva os exercícios 6 e 8, série 10.
Resolva os exercícios 11 e 14, série 10.
ANGLO VESTIBULARES
Aulas 29 e 30
DINÂMICA DO MOVIMENTO CIRCULAR EM PLANO VERTICAL
2. Uma esfera de massa m presa por um fio a um ponto fixo
(O) é abandonada em uma posição na qual ao fio está horizontal e esticado. Determinar, desprezando-se a resistência
do ar, a intensidade da força de tração no instante em que o
fio fica vertical.
Exercícios
1. Uma esfera de massa m presa por um fio a um ponto fixo
(0) é abandonada em uma posição na qual o fio está inclinado
de um ângulo α em relação à vertical. Considere o instante
em que o corpo passa pela posição na qual o fio está inclinado de um ângulo θ em relação à vertical (0 ⬍ θ ⬍ α) mostrada nas figuras, vindo da esquerda. Pede-se:
a) representar na figura (a) todas as forças que agem no
corpo, desprezando-se a resistência do ar.
b) representar na figura (b) a velocidade do corpo e classificar o movimento.
c) representar na figura (c) a resultante das forças que
agem sobre o corpo.
d) representar na figura (d) a aceleração bem como suas
componentes tangencial e centrípeta.
a)
b)
L
A
T
B
P
γ = aC
R
O
T
P
α
(εp + εc)A = (εp + εc)B
θ
mgL + 0 = 0 + 1/2 mV2
V 2 = 2gL
R = mγ
T – P = mac
T – mg = mV 2/L
T – mg = m (2 gL/L)
T = 3 mg
V
c)
d)
→
→
V
→
R = RT + RC
ac
γ
V=0
R = RC
aT
R = RT
ALFA-4 ★ 850750409
53
Vmáx
ANGLO VESTIBULARES
a) (Ep + Ec)C = (Ep + Ec)E
mgr + 0 = mgr + 0
a energia mecânica inicial é igual à final; OK
NE = m (v2/r + g ⋅ cos 90) = 0
NE = m (0 + 0) = 0 (está numa situação limite, mas
ainda é possível); OK
3. A pista da figura, mostrada em corte por um plano vertical, é
constituída de um trecho retilíneo (AT) em concordância com
um trecho circular (TF) de raio r. Não há atritos a considerar
e despreza-se a resistência do ar. Adotar g = 10 m/s2. Nessas
condições,
a) se um corpo é abandonado em C podemos garantir que
ele atinge o ponto E?
b) se um corpo é abandonado em B podemos garantir que
ele atinge o ponto F?
c) Se você respondeu negativamente à pergunta anterior,
determine a mínima altura do ponto A no qual deve ser
abandonado o corpo para que atinja o ponto
b) (Ep + Ec)B = (Ep + Ec)F
mg2r + 0 = mg2r + 0
a energia mecânica inicial é igual à final; OK
NE = m (v2/r + g ⋅ cos 180) = 0
NE = m [0 + g ⋅ (– 1)] ⬍ 0
Trata-se de uma situação física impossível.
A
F
c) NF = m (v2/r + g ⋅ cos 180) = 0
B
h
VF2/r + g ⋅ (– 1) = 0
E
VF2 = rg
(Ep + Ec)A = (Ep + Ec)F
C
T
mgh + 0 = mg2r + 1/2 m VF2
gh = 2gr + 1/2 rg
h = 2,5 r
D
θ
N
P ⋅ cos θ
P ⋅ sen θ
Para saber se um corpo pode ou não atingir um ponto da
pista devemos verificar duas coisas:
• Se ele tem energia mecânica suficiente para atingir o
ponto considerado.
• Se existe normal; sem normal não há tendência de penetração. (o caso de normal nula é a situação limite).
A normal em um ponto qualquer do trecho TF vale:
ORIENTAÇÃO DE ESTUDO
Livro 1 — Unidade II
Caderno de Exercícios — Unidade II
N – Pcos θ = mv2/r
N = m (v2/r + g cos θ) (1)
Tarefa Mínima
A expressão (1) mostra que:
AULA 29
1º-) se 0 ⭐ θ ⭐ 90, a normal existe mesmo que a velocidade seja nula. Portanto entre os pontos D e E,
mesmo que o corpo pare, ele não perde o contato
com a pista.
• Leia o texto Movimentos Verticais a seguir.
• Resolva os exercícios 19 e 25, série 10.
2º-) se 90 ⬍ θ ⭐ 180, a normal só, existe se
•
AULA 30
v2/r ⬎ gcosθ
Portanto entre os pontos E e F, se o corpo parar ele
perde o contato com a pista.
Tarefa Complementar
AULA 30
•
ALFA-4 ★ 850750409
Resolva os exercícios 20, 26 e 27, série 10.
54
Resolva os exercícios 24, 21, 22, 23, 31 e 33, série 10.
ANGLO VESTIBULARES
MOVIMENTOS VERTICAIS
Movimento Balístico
A trajetória de um corpo se movimentando nas proximidades da Terra, sob ação exclusiva de seu peso, só pode ser retilínea vertical ou parabólica.
Para obter uma trajetória diferente dessas, uma outra força tem de agir sobre o corpo.
É o que acontece, por exemplo, em um chute “com efeito”. A trajetória não é nem retilínea vertical nem parabólica. A outra força é exercida pelo ar.
Pistas Contidas em Planos Verticais
Vamos agora estudar exemplos nos quais a outra força é aplicada por um apoio. Vamos nos restringir ao caso em que o movimento está
contido em um plano vertical.
1º- Exemplo: desejamos que o corpo abandonado em um ponto A atinja um ponto B percorrendo uma trajetória retilínea não vertical (figura da
esquerda). Nesse caso, não há dúvida quanto à escolha do apoio: deve ser como o indicado na figura da direita.
A
A
Vo
Vo
B
B
2º- Exemplo: O corpo é lançado de um ponto A e desejamos que atinja em trajetória retilínea o ponto B, acima de A (figura da esquerda). Nesse
caso também não há dúvida: o apoio deve ser como o indicado na figura da direita.
B
B
Vo
Vo
A
A
3º- Exemplo: O corpo é abandonado de um ponto A e desejamos que atinja o ponto B em trajetória circular de raio r (figura da esquerda).
Continua não havendo dúvida: o apoio deve ser como o indicado na figura da direita.
A
A
B
B
Antes de apresentar o quarto exemplo, uma convenção e dois comentários.
CONVENÇÃO:
Tracejado indica a trajetória desejada
Contínuo indica trajetória que o corpo teria se não existisse o apoio.
Traço contínuo dentro de um tubo branco indica a penetração (imaginária)
do corpo no apoio.
ALFA-4 ★ 850750409
55
ANGLO VESTIBULARES
O primeiro comentário se refere à existência da normal. O apoio exerce uma força de contato que pode ser decomposta em normal e atrito. A componente normal só existe quando há tentativa de penetração. Para saber se existe normal represente a trajetória que o corpo teria se não existisse o
apoio e verifique se essa trajetória penetra ou não no apoio. Confira as figuras.
A
B
A
B
A
B
O outro comentário diz respeito ao cálculo da normal. Para facilitar o cálculo da normal vamos decompor o peso nas direções tangente (Px) e
normal à trajetória (Py).
N
N = Py
N = Py
R = Px
Py
R = Px
Py
Py
Px
P
P
P
Se a trajetória é retilínea, a normal e a componente
Py se equilibram. Logo, nos exemplos 1 e 2:
Se a trajetória é circular, a resultante das forças
normais à trajetória é para o centro e tem intensidade mV2/r, sendo r o raio da curva e m a massa do corpo.
Logo, no terceiro exemplo:
N = Py
N – Py = m ⋅ V2/r
4º- Exemplo: O corpo é lançado de um ponto A e desejamos
que atinja B em trajetória circular de raio r. Como deveria ser o
apoio nesse caso?
A resposta é: depende da trajetória que o corpo teria sem a
existência do apoio.
V0
A
B
r
Primeiro Caso
A trajetória desejada está acima daquela que o corpo teria se não existisse apoio. Nesse caso o apoio teria de estar sob o corpo, como mostra a
figura da direita.
V0
V0
A
B
B
A
r
r
ALFA-4 ★ 850750409
56
ANGLO VESTIBULARES
Segundo Caso
A trajetória desejada está abaixo daquela que o corpo teria se não existisse apoio. Nesse caso o apoio teria de estar sobre o corpo, como mostra a figura
da direita.
V0
V0
A
A
B
B
r
r
Vamos calcular a normal em um ponto qualquer da pista em cada um dos casos.
N
Px
Px
Py
θ
N
Py
B
A
θ
P
θ
P
Py – N = mV2/r
N = m(g cos θ – V2/r)
Py + N = mV2/r
N = m(V2/r – g cos θ)
1) Quanto maior o ângulo θ, mais baixo está o corpo e menor é a normal.
O ponto mais baixo é o mais crítico.
2) Quanto maior a velocidade, menor a normal.
3) Existe uma velocidade máxima para passar em um determinado
ponto da pista. É aquele para o qual a normal é nula.
4) Quanto menor o ângulo θ, mais alto está o corpo e menor é a normal.
O ponto mais alto é o mais crítico.
5) Quanto maior a velocidade maior a normal.
6) Existe uma velocidade mínima para passar em um determinado
ponto da pista. É aquele para o qual a normal é nula.
0 = m (g cos θ – V 2máx /r
0 = m(V2/r – g cos θ)
Vmáx =
ALFA-4 ★ 850750409
rgcos θ
Vmín =
57
rgcos θ
ANGLO VESTIBULARES
Aulas 31 e 32
ATRITO E PROBLEMAS GERAIS DE DINÂMICA
Escorregamento: É o movimento relativo entre as superfícies
de contato.
Atrito (ou força de atrito ou componente tangencial da força de contato): É a componente da força de contato, causada
pela interpenetração das rugosidades das superfícies de contato,
que impede ou dificulta o escorregamento.
→
C
N
T
A
(1)
T
mg
(2)
→
Mg
N
→
A
AC = 0,3 ⋅ 100 = 30 N
T
A
(1)
AMAX = 0,35 ⋅ 100 = 35 N
caso a
T
a) M = 2 kg. P = 20 N, logo
a força de atrito consegue
equilibrar a solicitadora:
γ = 0; A = 20 N
rugosidade
interpenetradas
Condições de Existência:
• Contato entre superfícies rugosas.
• Escorregamento ou tendência.
• Normal (compressão).
(2)
Mg
T
A
(1)
b) M = 3,5 kg. P2 = 35 N,
o sistema está na
iminência de escorregar:
γ = 0; A = AMAX = 35 N
Como marcar:
• direção: tangente (paralela) à superfície de contato.
• sentido: contrário ao escorregamento ou tendência.
caso b
T
(2)
Mg
Como calcular:
ATRITO ESTÁTICO: AE ⭐ μe N
A
AE = μe N na iminência de escorregar.
c) M = 10 kg. P2 = 100 N.
A = AC = 30 N, pois o sistema começa a escorregar.
ATRITO CINÉTICO: AC = μcN
Exercícios
T
(2)
Mg
1. O coeficiente de atrito estático entre o bloco (1), de massa
10kg, e a superfície de apoio vale 0,35 e o cinético 0,30.
Por intermédio de um fio e polia ideais liga-se o bloco (1) a
um bloco (2) de massa M. Supondo g = 10m/s2 e abandonando o sistema a partir do repouso, determinar a aceleração
adquirida pelo conjunto e a intensidade da força de atrito trocada entre o bloco (1) e o plano, nos seguintes casos:
a) M = 2 kg
b) M = 3,5 kg
c) M = 10 kg
ALFA-4 ★ 850750409
T
(1)
P2 – T = m ⋅ |a|
T – AC = m ⋅ |a|
⎢
⎢
⎢
⎢
⎢
100 – T = 10 ⋅ |a| ⎥
⎥
T – 30 = 10 ⋅ |a| ⎥
⎥
70 = 20|a| ⎥
|a| = 3,5 m/s2
58
ANGLO VESTIBULARES
2. Ainda com relação à questão anterior. Suponha que a massa
do corpo 2 possa variar entre os valores 0 e 45kg. Esboçar o
gráfico da intensidade da força de atrito que realmente age
no corpo 1 em função da força solicitadora (peso do corpo 2).
3. Um corpo de massa m desliza sobre um plano horizontal
passando por um ponto A com velocidade 20m/s. Sabendose que o coeficiente de atrito cinético entre o corpo e o apoio
é 0,4 determinar:
a) a aceleração do corpo.
b) a distância que o corpo percorre até parar.
A (N)
N
30
v=0
V0
A
20
P
Δs
10
0
10
20
30
40
R = mγ
AC = m |a|
F (N)
μcmg = m |a|
|a| = μcg
|a| = 4 m/s2
b) V 2 = V 02 + 2 aΔs
0 = (20)2 – 2 ⋅ 4 Δs
Δs = 50m
ALFA-4 ★ 850750409
59
ANGLO VESTIBULARES
4. (FGV-SP/corrigido) Um automóvel de 1720 kg entra em
curva plana horizontal de raio r = 200m, a 180km/h. Sabendo que o coeficiente de atrito entre os pneus do automóvel e a rodovia é igual a μe = 0,3 (coeficiente de atrito
estático) e μc = 0,2 (coeficiente de atrito cinético), está correto afirmar que:
a) Para que um corpo percorra uma trajetória circular com
velocidade escalar constante, a resultante das forças que
agem sobre ele deve ser nula.
b) Para que o carro faça uma curva em uma pista plana horizontal com velocidade escalar constante, a resultante das
forças que agem sobre ele deve ser a componente radial
do atrito.
c) O automóvel está a uma velocidade segura para fazer a
curva.
d) O automóvel irá derrapar radialmente para fora da
curva.
a) Errado. A resultante é radial para dentro da curva.
b) Certo. A resultante é radial para dentro da curva.
c) Errado. R = m(V2/r)
μmg = m(V2/r) ∴ V = 公僒
μ僒
rg ⬇ 24,5 m/s
V (máxima velocidade com que o veículo pode fazer a
curva).
d) Errado. Pelo Princípio da inércia, o veículo escapa da
curva tangencialmente.
N
r = 200 m
R=A
P
ORIENTAÇÃO DE ESTUDO
Livro 1 — Unidade II
Caderno de Exercícios — Unidade II
Tarefa Mínima
AULA 31
•
•
Leia os itens 1, 2 e 3, cap. 7.
Resolva os exercícios 2, 4, 5, 24 e 25, série 11.
AULA 32
•
Resolva os exercícios 6, 10 e 11, série 11.
Tarefa Complementar
AULA 32
•
ALFA-4 ★ 850750409
60
Resolva os exercícios 34, 39, 44 e 48, série 11.
ANGLO VESTIBULARES
Aulas 33 e 34
QUEDA LIVRE E LANÇAMENTO VERTICAL
2. A aceleração é constante e não depende da massa,
mas o sinal da aceleração depende da orientação da
trajetória. No caso da queda livre, é positiva se a trajetória é orientada para baixo.
3. A classificação do movimento em acelerado ou retardado só leva em conta o módulo da velocidade. Portanto não depende da orientação da trajetória. No
caso da queda livre, o movimento é sempre acelerado.
A afirmação II estaria correta no caso de existir resistência do ar.
Um corpo em queda ou lançado verticalmente no vácuo
(ou em circunstâncias tais que a resistência do ar possa ser
desprezada) adquire movimento uniformemente variado, com
aceleração em módulo igual a g e que não depende da massa
do corpo.
Exercícios
Nas 3 questões que se seguem, é sempre discutida uma
mesma situação física: um corpo é abandonado a partir do
repouso no vácuo. Considerar o campo gravitacional constante.
Em cada uma delas são feitas 4 afirmações que devem ser
respondidas de acordo com o seguinte critério:
a) se nenhuma das afirmações está correta;
b) se apenas uma das afirmações está correta;
c) se apenas duas das afirmações estão corretas;
d) se apenas três das afirmações estão corretas;
e) se todas as afirmações estão corretas.
1. A respeito da velocidade do corpo:
I — é constante. E
II — é crescente em módulo. C
III — é sempre positiva. E
IV — pode ser positiva ou negativa, dependendo da orientação da trajetória. C
(C )
2. A respeito da aceleração do corpo:
I — é constante e não depende da massa. C
II — é crescente. E
III — é sempre positiva. E
IV — pode ser positiva ou negativa, dependendo da orientação da trajetória. C
(C )
3. A respeito do movimento adquirido pelo corpo:
I — é uniforme. E
II — inicialmente é acelerado e depois passa a ser uniforme. E
III — é acelerado. C
IV — pode ser acelerado ou retardado, dependendo da
orientação da trajetória. E
(B )
Comentários:
1. O módulo da velocidade é crescente, mas o sinal da
velocidade depende da orientação da trajetória. No
caso da queda livre, é positiva se a trajetória é orientada para baixo.
ALFA-4 ★ 850750409
61
ANGLO VESTIBULARES
4. Um corpo é abandonado a partir do repouso do alto de um
prédio de 490m de altura. Desprezar a resistência do ar.
(Adotar g = 9,8 m/s2)
Determinar:
a) O tempo de queda.
b) A velocidade com que chega ao solo.
5. Um corpo em queda livre no vácuo, nas proximidades de um
planeta desconhecido, percorre 3m no primeiro segundo de
sua queda. Qual a distância percorrida durante o terceiro
segundo? Esboçar o gráfico da velocidade em função do
tempo.
Equação horária da queda livre:
⎛ ⎞
S = ⎜ 1 ⎟ gt2
⎝2⎠
0
para:
⎛1⎞
t = 1 s ⇒ S1 = ⎜ ⎟ gt2 ⇒
⎝2⎠
490 m
⎛1⎞
⇒ 3 = ⎜ ⎟ g (1)2 ⇒
t
⎝2⎠
⇒ g = 6 m/s2
⎛1⎞
t = 2 s ⇒ S2 = ⎜ ⎟ g(2)2 = 12 m
⎝2 ⎠
Adotando-se a origem no ponto onde o corpo é abandonado e orientando-se a trajetória para baixo, podemos
escrever:
⎛1⎞
t = 3 s ⇒ S3 = ⎜ ⎟ g(3)2 = 27 m
⎝2⎠
⎛1⎞
a) S = ⎜ ⎟ gt2
⎝2⎠
⎛
O 3º- segundo é o intervalo de tempo compreendido em
t = 2 s e t = 3 s, logo, d = S3 – S2 = 15 m.
d = 15 m
⎞
490 = ⎜ 1 ⎟ 9,8 t2
⎝2 ⎠
t = 10 s
y
b) v = v0 + at
v = 0 + 9,8 (10)
v = 98 m/s
x
x
x
x
x
x
x
x
0
t
x
x
x
2t
x
x
x
x
3t
x
x
x
x
x
x
4t
x
x
x
x
5t
t
Observe que entre os instantes: O a t o corpo percorre x,
de t a 2t o corpo percorre 3x, de 2t a 3t o corpo percorre 5x, e assim por diante.
Essa propriedade é conhecida como regra de Galileu.
ALFA-4 ★ 850750409
62
ANGLO VESTIBULARES
g) v = 20 – 10 (7) = – 50 m/s
6. Num local onde g = 10m/s2, um corpo é lançado verticalmente para cima com velocidade inicial igual a 20m/s. Desprezando-se as forças trocadas com a atmosfera e sabendo-se que no ponto de partida ele está a 105 m acima do
solo, determinar:
a) a que altura ele se encontra no instante t = 1s.
b) a velocidade neste instante.
c) em que instante ele atinge a altura máxima.
d) o valor da altura máxima.
e) o tempo que demora para passar novamente pelo ponto de partida.
f) em que instante atinge o solo.
g) a velocidade com que o corpo chega ao solo.
h) construir os diagramas s × t, v × t.
h)
t
S
0
105
1
120
2
125
3
120
4
105
5
80
6
45
7
0
s (m)
100
50
0
20
10
0
– 10
– 20
– 30
– 40
– 50
1
t (s)
2
3
4
5
6
7
8
2
3
4
5
6
7
8 t (s)
v (m/s)
1
ORIENTAÇÃO DE ESTUDO
Livro 1 — Unidade I
Caderno de Exercícios — Unidade I
⎛1⎞
S = S0 + v0t + ⎜ ⎟ a t2
⎝2⎠
Tarefa Mínima
S = 105 + 20 t – 5 t2
v = v0 + at
v = 20 – 10 t
AULA 33
•
•
a) S = 105 + 20 (1) – 5 (1)2 = 120 m
b) v = 20 – 10 (1) = 10 m/s
c) 0 = 20 – 10 t ⇒ t = 2 s
d) S = 105 + 20 (2) – 5 (2)2 = 125 m
e) S = S0 = 105 = 105 + 20 t – 5 t2 ⇒
AULA 34
•
•
Leia o item 2 (só exercício 2), cap. 5.
Resolva os exercícios 1, 7 e 3, série 5.
Tarefa Complementar
⇒ t = 0; t = 4 s
AULA 34
f) S = 0 = 105 + 20 t – 5 t2 ⇒
⇒ t = – 3s ; t = 7 s
ALFA-4 ★ 850750409
Leia os itens 1 e 2 (só exercício 1), cap. 5.
Resolva os exercícios 1 a 4, série 4.
63
•
Resolva os exercícios 5 a 8, série 4.
•
Resolva os exercícios 4, 5 e 6, série 5.
ANGLO VESTIBULARES