Untitled

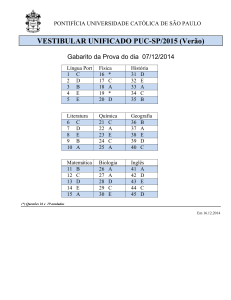
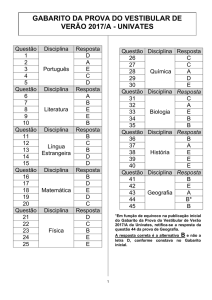
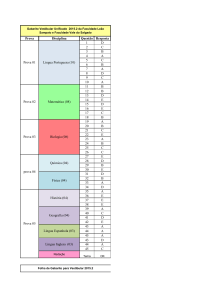
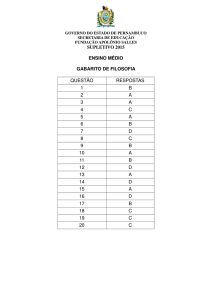
Vestibular 2012 – UPE
Como o sistema está em equilíbrio, a força resultante
sobre ele é nula. Ou seja,
01. Considere um rio de margens paralelas, cuja
distância entre as margens é de 140 m. A velocidade
da água em relação às margens é de 20 m/s. Um bote
cuja velocidade em relação à água é 10 m/s atravessa
o rio de uma margem à outra no menor tempo
possível. Assinale a alternativa que corresponde a este
tempo em segundos.
A) 6,36
B) 12,36
C) 13
D) 14
E) 14,36
∙
Para atravessar o rio no menor tempo possível o bote
deve ter uma velocidade de 10 m/s em relação ao rio e
perpendicular as margens.
A velocidade da correnteza não influi na travessia do
rio. Então realizando as contas temos:
∆
140
⇒ ∆
10
∆
∙
→
∙
2∙
∙
03. Uma esfera de massa m = 1,0 kg,
inicialmente em repouso, a uma altura h
= 6,0 m, é abandonada sobre uma mola
ideal de constante elástica k = 1,0 x 10²
N/m, como ilustra a figura a seguir.
Considere a aceleração da gravidade g =
10
m/s².
Desprezando
quaisquer
dissipações de energia, assinale as
proposições a seguir:
I. A velocidade da esfera começa a diminuir a partir
do instante em que a esfera atinge a mola.
II. A máxima deformação da mola é xmáx = 1,0 m.
III. A deformação da mola no instante em que a
velocidade da esfera for máxima é x = 10 cm.
IV. A velocidade máxima da esfera é vmáx = 11 m/s.
V. A velocidade com que a esfera é arremessada
para cima no instante em que perde o contato
0,5
com a mola é v = 2(30) m/s.
Gabarito: D
∆
⇒ ∆
∆
∙
Estão CORRETAS
A) I, II, III, IV e V.
B) I, III e IV.
C) I, II, IV e V.
D) III, IV e V.
E) II, IV e V
02. Um corpo de massa m está suspenso por duas
molas ideais, paralelas, com constantes elásticas k e
deformadas de d. Sabendo que o sistema se encontra
em equilíbrio, assinale a alternativa que expressa k.
Dado: Considere a aceleração da gravidade g.
A) 2mg/d
B) mg/d
C) mg/2d
D) 2d/mg
E) d/mg
Gabarito: D
Gabarito: C
No corpo de massa m atuam três
forças: o peso (dirigido para baixo)
e as forças elásticas de cada mola
(dirigidas para cima).
I. FALSO
A velocidade da esfera só começa a diminuir depois
do instante que a força Peso se iguala com a força
elástica.
2
Profs. Carlos Alberto / José Ranulfo
http:// www.fisicacomcarlos.blogspot.com
Vestibular 2012 – UPE
1 ∙ 28*
1 ∙ 10 ∙ 1,2
2
100 ∙ 1,2*
2
0,5 ∙ 28*
II. FALSO
A deformação máxima ocorre com o corpo alcança a
linha C. Fazendo as contas da linha R até a linha C
temos:
!"#
28*
28
!"$
28
Na linha R só temos energia potencial gravitacional
e na linha C só temos energia potencial elástica.
∙
∙ %&
1 ∙ 10 ∙ %6
60
∙ '(
2
'( )
'( )
10'(
50 ∙ '( * - 10'( - 60
28
III. VERDADEIRO
0
C)
D)
A deformação da mola no instante em que a
velocidade da esfera é máxima ocorre quando a
força peso for igual a força elástica e isso ocorre na
linha B da figura, ou seja:
'
IV. VERDADEIRO
∙
∙ %&
1 ∙ 10 ∙ %6
!"#
' )
0,1)
60,5
101
!"0
∙'
2
As forças que atuam na roda são ilustradas abaixo:
*
100 ∙ 0,1*
2
∙ 2*
2
1 ∙ 2*
2
121
2
2
∙ '7 *
2
Para que a roda seja erguida sobre o degrau, é
necessário que ela rotacione. Assim, devemos
identificar as forças que atuam na roda e verificar
quais causam torque (também conhecido por momento
da força).
100 ∙ '
0,5 ∙ 2 *
2*
V. VERDADEIRO
Gabarito: C
∙'
0,1
√121
Na eminencia da rotação, o torque devido a força F
(sentido horário) é igual ao torque devido ao Peso
(sentido anti-horário). Perceba que a força Normal não
realiza torque, pois sua linha de ação passa pelo eixo
de rotação.
!"6
Lembrando que o momento de uma força em relação
a um polo é definido como sendo o produto da força
(em módulo) pela distância entre o polo e o ponto de
11 /5
!"$
2 ∙ %30)<,= /5
√3/3
E)
/0
1 ∙ 10
2√30 /5
√3/2
/2
√3
A)
B)
1,2
∙
:2* ∙ 30
04. A figura abaixo ilustra uma roda de raio R e massa
m. Qual é o módulo da força horizontal F, necessária
para erguer a roda sobre um degrau de altura h = R/2,
quando aplicada no seu eixo? Considere a aceleração
da gravidade g.
Resolvendo a equação do 2º grau
'(
120
que pode ser escrito como
*
100 ∙ '( *
2
50 ∙ '( *
72 - 12
∙ 28*
2
∙
∙ '7
Profs. Carlos Alberto / José Ranulfo
3
http:// www.ranulfofisica.blogspot.com.br
Vestibular 2012 – UPE
aplicação da força (ou linha de ação da força
aplicada). Assim,
>?
∙'
∙ & →
>@
06. Um olho de uma pessoa pode ver nitidamente
objetos situados desde o infinito, que é o ponto
remoto, até 20 cm, que é o ponto próximo. Qual a
amplitude de acomodação visual de sua vista, isto é, a
variação da vergência de seu cristalino, quando o
objeto se movimenta entre o ponto próximo e o ponto
remoto?
A) 0,05 di.
B) 20 di.
C) 0,20 di.
D) 5 di.
E) Infinita.
∙ A/2
'
Para determinar o valor de x usamos o teorema de
Pitágoras:
A*
'*
BA * -
&* → '
3A *
B
4
'
Substituindo em F, obtemos
C
A√3
2
A*
4
Gabarito: D
Equação de Gauss:
√D
sendo
1
HPQóST"U
Gabarito: A
Como MN PQóS.
Aplicando o Princípio de Pascal temos que a pressão
do lado direito é igual a pressão do lado esquerdo,
com isso temos
I∙
J
E*
1
MN
1
HPQóST"U
-
1
HQ/"UVU
1
1
1
- N
e
0,2 M PQóS.
HQ/"UVU
∆
GF
∆
√AE
F
1
M
onde M é a distância do objeto a lente, e MN a distância
da imagem a lente.
A vergência de uma lente é obtida pelo inverso do
foco:
1
H
Ponto remoto: MN tende a infinito;
Ponto próximo: MN 201
0,2 ;
05. Na prensa hidráulica, ilustrada na figura a seguir, o
êmbolo menor tem raio r, e o êmbolo maior, raio R. Se
for aplicada, no êmbolo menor, uma força de módulo
F, qual a intensidade da força no êmbolo maior?
A * /E *
A)
B)
E * /A *
C) A/E
D) E/A
E)
1
H
1
1
- N
0,2 M PQóS.
1
0-
1
M′Q/".
M′Q/".
MN Q/". (tamanho do olho é o mesmo)
∆Z
[,
\ ]
07. Um feixe de luz monocromática de comprimento de
onda λ atravessa duas fendas separadas de uma
distância d como ilustrado a seguir. Uma tela de
observação é posicionada a uma distância D para
estudar os padrões de interferência.
Considere que D >> d e utilize aproximações de
ângulos pequenos.
H
G
H
I ∙ A*
C∙K
L
4
Profs. Carlos Alberto / José Ranulfo
http:// www.fisicacomcarlos.blogspot.com
Vestibular 2012 – UPE
I. FALSO
13 ∙
_
II. VERDADEIRO
Primeira franja escura:
_b
Analise as seguintes proposições:
I. A distância entre o 7º mínimo e o máximo central
vale 7λ^/2 .
II. A distância entre franjas escuras consecutivas é
uma constante.
III. Essa experiência comprova o caráter corpuscular
da luz.
IV. O tamanho das fendas não altera o padrão de
interferência no anteparo.
V. A distância entre o 2º mínimo e o 1º mínimo vale
Segunda franja escura:
_*
Terceira franja escura:
_c
Quarta franja escura:
_d
λ^/
a
2
∙_
^
13a^
2
1a^
2
3a^
2
5a^
2
7a^
2
Se fizermos a subtração entre as distâncias de
duas franjas escuras temos
Estão INCORRETAS
A) I e V, apenas.
B) I, II, III e IV.
C) I, II e V, apenas.
D) I, III e IV, apenas.
E) I, III e V, apenas.
_* - _b
_c - _*
3a^ 1a^
2
2
5a^ 3a^
2
2
2a^
2
2a^
2
a^
a^
1e`5 f` g
1e`5 f` g
Se repetirmos isso para os demais acontecerá a
mesma coisa.
Gabarito: D
III. FALSO
Comprova o caráter ondulatório da luz.
IV. FALSO
_
`a^
2
A equação acima mostra a posição das franjas
dependente da distancia entre as fendas.
V. VERDADEIRO
_* - _b
∙_
∆ ^
(diferença entre os caminhos)
∆
`∙
a
2
3a^ 1a^
2
2
2a^
2
a^
1e`5 f` g
08. Um bloco de ferro de 500 g a 42°C é deixado num
interior de um recipiente de capacidade térmica
desprezível, contendo 500 g de água a 20°C. Qual é a
temperatura final de equilíbrio?
Dados: Calor Específico do Ferro: cFe = 0,1 cal/g°C
Calor Específico da Água: cágua = 1 cal/g°C
onde n assume valores pares para máximos (franjas
claras) e valores impares para mínimos (franjas
escuras).
5
Profs. Carlos Alberto / José Ranulfo
http:// www.ranulfofisica.blogspot.com.br
A)
B)
C)
D)
E)
Vestibular 2012 – UPE
100 - 90
∆h
10°C
12°C
15°C
20°C
22°C
∆h
II. VERDADEIRO
s
Gabarito: E
s
10r
hb - h*
10r
Como a água e o ferro estão em um recipiente de
capacidade térmica desprezível, o calor cedido por um
vai ser absorvido pelo outro. Sendo assim, temos
hájkl
hm/QQU
0.
É importante perceber que, a água por possuir uma
temperatura inferior ao do ferro, irá receber calor (Q >
0) e irá esquentar. Enquanto que o ferro perderá calor
(Q < 0), esfriando-se.
Fazendo as contas, temos:
8
∙ 18 ∙ ∆n8
500 ∙ 1 ∙ %n? - 20)
500n? - 10000
550n?
n?
oC
?
∙ 1? ∙ ∆n?
0
500 ∙ 0,1 ∙ %n? - 42)
50n? - 2100
12100
0
0
III. VERDADEIRO
A eficiência da um refrigerador é dado por
g
12100
550
'% )
p
9
I
4 ∙ cos w
2
Ix
onde x(t) é dado em metros e t em segundos, analise
as seguintes afirmativas:
I. A amplitude é 4 m.
II. O período é 4 s.
III. A frequência do movimento oscilatório é 0,25 Hz.
Está CORRETO o que se afirma em
A) I, apenas.
B) I e II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
Está CORRETO o que se afirma em
A) I, apenas.
B) I e II, apenas.
C) I e III, apenas.
D) II e III, apenas.
E) I, II e III.
Gabarito: E
A função horária equação da posição de uma partícula
em Movimento Harmônico Simples é
'% )
G ∙ cos%y
z)
onde G é a amplitude do movimento, yé a frequência
(ou velocidade) angular e z a constante de fase.
Gabarito E
∆h
90
10
10. Dada a equação horária da elongação de um MHS
09. Num refrigerador, para 90 J retirados, em cada
ciclo da máquina, 100 J são enviados do congelador
para o meio ambiente. Sobre isso, analise as
seguintes alternativas:
I. A variação de calor entre as fontes quente e fria é
10 J.
II. O trabalho do compressor em cada ciclo é 10 J.
III. A eficiência desse refrigerador é 9.
I. VERDADEIRO
h*
s
hb - h*
6
Profs. Carlos Alberto / José Ranulfo
http:// www.fisicacomcarlos.blogspot.com
Vestibular 2012 – UPE
I. VERDADEIRO
Por comparação, vemos que a amplitude
movimento é G
4m.
O potencial da nova esfera maior é dado por
G do
e o potencial das esferinhas é dado por
II. VERDADEIRO
Novamente por comparação, temos que a
|
frequência angular é y
rad/s. A frequência
*
Então a esfera maior fica
angular se relaciona com o período por
2I
n
y
Assim,
n
2I
y
2I
I
2
III. VERDADEIRO
1
4
H
´
Z´
1/n.
D)
E)
†∙`∙„
√` ∙ E
ƒ
0,25Hz
´
`
∙ƒ
√`
Z ∙ :‡
D
12. Um fio metálico de resistência R e onde passa uma
corrente I é esticado de modo que seu comprimento
triplique e o seu volume não varie no processo. A
tensão aplicada no fio metálico é a mesma para ambos
os casos. Assinale a alternativa que corresponde à
nova resistência e corrente elétrica, quando o fio é
esticado.
A) 6R; I/3
B) 6R; I/6
C) 3R; I/6
D) 3R; I
E) 9R; I/9
11. Imagine uma pequena gota esférica de um fluido
incompressível, com uma certa carga que tem um
potencial eletrostático V em sua superfície. Se n gotas
idênticas e de mesma carga desse fluido se unem para
formar uma gota esférica maior, qual o potencial
elétrico na superfície da nova gota?
A)
B)
∙ `‚b
C)
†∙„
E
Combinando com o potencial das esferinhas, por
fim ficamos com
4s
A frequência é o inverso do períodoH
Assim,
†∙`∙„
A
´
∙ √`
ƒ
∙ √`*
ƒ
∙ √`‚b
ƒ
Gabarito: E
Para que o volume permaneça o mesmo, quando
triplicamos o comprimento a área é reduzida a um
terço ( eˆ‰ g ÁEgf ‹ Œe ME• g` e).
Gabarito: D
Considere que a esfera maior (M) tem um volume n
vezes o volume da esferinha (m), assim
>
4
I ∙ Ac
3
A
`∙
4
I ∙ Ec
3
√` ∙ E
ƒ
No primeiro caso, temos
1ª Lei de Ohm:
relação entre os raios da esfera maior (R) e a
esferinha (r).
A. Ž → Ž
Considere que a quantidade de carga dessa nova
esfera é dado por
2ª Lei de Ohm:
onde n e q é o numero de pequenas esferas e suas
respectivas cargas.
No segundo caso, temos
h
`∙„
A
••
G
A
7
Profs. Carlos Alberto / José Ranulfo
http:// www.ranulfofisica.blogspot.com.br
Vestibular 2012 – UPE
2ª Lei de Ohm:
AN
••
→ AN
GN
• ∙ 3•
GN
3
N
N
KN
1ª Lei de Ohm:
9 ∙
‘K
AN . ŽN → ŽN
’N
AN
’
‘
= 1,0 ohm, R2 = 3,0 ohms e R = 1,0 ohm, conforme
mostrado na figura a seguir:
••
G
9A
Analise as seguintes proposições:
I. A corrente que passa pelo resistor R1 vale 6 A.
II. O sentido da corrente que passa pelo resistor R2
é da esquerda para a direita.
III. A potência dissipada no resistor R2 vale 12 W.
IV. O sentido da corrente que passa pelo resistor R é
de cima para baixo.
13. Um motor elétrico sob tensão 220 V é alimentado
por uma corrente elétrica de 10 A. A potência elétrica
útil do motor é de 2000 W. Assinale a alternativa que
corresponde à força contraeletromotriz, em volts, à
resistência interna do motor, em ohms, e ao
rendimento elétrico do motor, respectivamente.
A) 200; 2; 0,80
B) 200; 2; 0,91
C) 400; 4; 1
D) 400; 4; 0,80
E) 400; 4; 1,5
Estão CORRETAS
A) I, II, III e IV.
B) II, III e IV.
C) I, II e III.
D) II e IV.
E) I, III e IV.
Gabarito B
Gabarito: E
Considerando o motor como um receptor elétrico,
temos que a potencia útil é dada por:
Como o circuito acima não pode ser reduzido a um
circuito simples, vamos utilizar as duas Leis de
Kirchhoff.
”∙•
“
onde ε e a força contraeletromotriz. Fazendo as contas
2000
•
” ∙ 20
[[Z
Agora vamos considerar a função de receptor
–
”
E∙•
onde é a resistência interna do receptor. Fazendo as
contas
220
L
200
E ∙ 10
—
• Lei dos nós:
• Malha 1:
O rendimento de um receptor é dado por
˜
Me . ú •ˆ
Me . e fˆ
›
”∙•
–∙•
”
–
‘ %
200
≅ 0,91
220
• Malha 2:
•b
•*
!b - Ab ∙ •b - A ∙ •c
0
A ∙ •c - A* ∙ •* - 14
0
•b
•c
•c - 3•*
14. Um circuito com duas malhas contém duas fontes
de tensão constante E1 = E2 = 14 V e três resistores R1
•c %1)
14%2)
14%3)
8
Profs. Carlos Alberto / José Ranulfo
http:// www.fisicacomcarlos.blogspot.com
Vestibular 2012 – UPE
Temos três equações e três incógnitas. Vamos então
resolver esse sistema.
Substituindo (1) em (2), temos
•*
2•c
•*
14
14 - 2•c %4)
Substituindo (4) em (3), temos
•c - 3%14 - 2•c )
]D
14 → •c - 42
•ž
6•c
14
Substituindo o valor de •c em (4)
Então
I. VERDADEIRO
]
]
- ž
Ÿž
A corrente que passa pelo resistor R1 é •b e vale 6 A.
II. FALSO
Adotamos o sentido da corrente •* como sendo da
esquerda para direita e achamos seu sinal negativo.
Isso significa que o sentido real dela é da direita para
esquerda.
III. VERDADEIRO
IV. VERDADEIRO
¤< cotg§
"j¨
A)
S© ª
"j¨
B)
S© ª
C)
A* ∙
•**
3∙2
*
12W
cotg * §
¤< cotg§ -
D)
¤< cotg§ -
E)
Adotamos o sentido de •c como sendo de cima para
baixo e achamos seu valor positivo.
cotg§
"j¨
S© ª
"j¨
S© ª
cotg§
cotg * §
Gabarito: E
Calculando como se comporta a variação do fluxo
magnético pelo tempo vamos ter a força eletromotriz
(Lei de Faraday) temos:
15. Uma barra condutora homogênea de comprimento
y e massa m é apoiada num suporte como mostrado
na figura a seguir. Esse suporte consiste em um ramo
de circuito em forma de U e de resistência R, isolado
da superfície da Terra. A barra está a uma altura x em
”
¢¢£
relação ao lado inferior do U. Um campo magnético ¡
com sentido para fora do plano do papel (sentido
positivo) é aplicado na região cujo módulo varia com o
tempo t, conforme o gráfico abaixo. O módulo do
campo em t = 0 vale B0. A partir de que instante, a
barra não sentirá as forças de reação normal do
suporte (ou seja, a barra estará quase levitando)?
Dado: Considere a aceleração da gravidade g.
onde
-
∆Φ
∆
-
∆%B ∙ A)
∆
∆B
∆
-A ∙
∆B
∆
' ∙ _ ∙ tan §
- tan §
(o negativo aparece por causa da inclinação da reta)
Considerando a lei de Ohm
•
”
A
' ∙ y ∙ tan §
A
•
Para que a barra fique quase levitando o módulo da
força magnética fica igual ao módulo da força Peso.
Então
9
Profs. Carlos Alberto / José Ranulfo
http:// www.ranulfofisica.blogspot.com.br
Vestibular 2012 – UPE
"
V. Esse princípio se torna irrelevante na
interpretação de experiências que lidam com
objetos macroscópicos, mas se torna relevante na
interpretação de experiências que lidam com
partículas subatômicas, como os elétrons.
¤∙•∙_
∙
tan §
∙_
A
' ∙ _ ∙ tan §
∙_
¤∙
A
∙ ∙A
tan § ∙ ' ∙ _ *
¤∙
¤
Estão CORRETAS
A) I, II, III, IV e V.
B) I e II, apenas.
C) I, II e V, apenas.
D) I, II, IV e V, apenas.
E) I, II e IV, apenas.
O campo magnético vale para quando a barra começa
a levitar.
Tirando do gráfico a equação do campo magnético
¤
¤
¤<
∆B
∙
∆
Gabarito: D
I. VERDADEIRO
¤< - tan § ∙
Este é o enunciado do Princípio da Incerteza.
Considerando o campo onde a barra começa a levitar
∙ ∙A
tan § ∙ ' ∙ _ *
II. VERDADEIRO
¤< - tan § ∙
Essa afirmativa é um exemplo que confirma o
enunciado (afirmativa I).
¤<
∙ ∙A
*
tan § tan § ∙ ' ∙ _ *
¡[ °±
²-
∙ ∙K
°±
³∙´
III. FALSO
A imprecisão não tem nada a ver com os
instrumentos de medida.
²
IV. VERDADEIRO
O observador interfere na medida quando tenta
realizá-la. Isto é um fundamento básico do princípio.
16. Sobre o Princípio da Incerteza de Heisenberg,
analise as proposições a seguir:
I. Se uma medida da posição for feita com precisão
∆x e se uma medida simultânea da quantidade de
movimento for feita com precisão ∆p, então o
produto das duas incertezas nunca poderá ser
menor do que &/4π, ou seja, ∆' ∙ ∆M µ &/4I.
II. Quanto maior a precisão na determinação da
posição do elétron, menor é a precisão na
determinação de sua velocidade (ou de sua
quantidade de movimento) e vice-versa.
III. O princípio afirma que há um limite real para a
precisão das medições simultâneas da posição e
da quantidade de movimento. Esse limite provém
da própria estrutura quântica da matéria e das
imperfeições dos instrumentos de medida
utilizados.
IV. O princípio fundamenta-se na ação do observador
sobre o objeto observado; logo, ele é uma
manifestação da impossibilidade de se ignorar a
interação entre o observador e o objeto
observado.
V. VERDADEIRO
Em corpos macroscópicos
observador é irrelevante.
a
interferência
do
10
Profs. Carlos Alberto / José Ranulfo
http:// www.fisicacomcarlos.blogspot.com