FATORAÇÃO

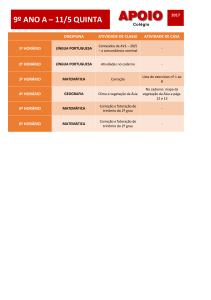
FATORAÇÃO
Os métodos de fatoração de expressões algébricas são:
Fator comum (coloca-se o fator comum em evidência);
Agrupamento de fatores comuns;
Trinômio Quadrado Perfeito;
Trinômio: x²+Sx+P = 0;
Diferença de dois quadrados (x²-y²);
Soma de dois cubos;
Diferença de dois cubos.
Definição de Fatoração
A fatoração é a transformação da soma e/ou subtração de vários termos em um produto de diversos fatores.
Vejamos alguns exemplos onde temos alguns dos principais tipos de fatoração:
Na sequência vemos como tratar cada um destes tipos de fatoração em particular.
A fatoração é um recurso que utilizamos na simplificação de sentenças matemáticas. Quando for o caso, podemos
utilizá-la na simplificação de uma fração ou de uma equação, por exemplo.
Fator Comum: ax + bx = x(a + b)
A forma mais básica de fatoração é a colocação de fatores comuns em evidência.
No exemplo abaixo o fator 5 é comum a todos os termos e por isto é possível colocá-lo em evidência:
Colocamos o fator 5 em evidência o destacando e o multiplicando pela a expressão quociente da divisão da sentença
original por tal fator, inserida entre parênteses:
Exemplos
Agrupamento: ax + bx + ay + by = (a + b)(x + y)
No tipo de fatoração por agrupamento não temos um fator que é comum a todos os termos, no entanto temos fatores
que são comuns a alguns termos e outros fatores que são comuns a outros termos.
Vejamos o exemplo abaixo:
Note que o fator x é comum aos dois primeiros termos, assim como o fator y é comum aos dois últimos termos, então
podemos colocá-los em evidência:
Veja que ainda temos o fator (4 + 6) em comum e que também pode ser colocado em evidência:
Assim sendo:
Obviamente, como mostrado abaixo, podemos continuar os cálculos somando 4 com 6, mas o foco aqui é a fatoração
em si:
No lugar dos fatores x e y, poderíamos evidenciar os fatores 4 e 6, visto que ambos são comuns ao fatores 4x e 4y, no
caso do 4 e6x e 6y, no caso do 6:
E ao colocarmos o fator (x + y) em evidência, chegamos ao mesmo resultado obtido anteriormente, apenas com uma
mudança na ordem dos fatores, que como sabemos não altera o produto:
Exemplos
Trinômio Quadrado Perfeito - Soma: a2 + 2ab + b2 = (a + b)2
Quando desenvolvemos o quadrado da soma de dois termos chegamos a um trinômio quadrado perfeito, que é o que
demonstra a sentença acima, só que temos os membros em ordem inversa. Então o quadrado da soma de dois
termos é a forma fatorada de um trinômio quadrado perfeito.
Como fatorar o trinômio abaixo?
Se o pudermos escrever como a2 + 2ab + b2 estaremos diante de um trinômio quadrado perfeito, que fatorado é igual
a(a + b)2.
Obtemos o valor de a extraindo a raiz quadrada de x2 no primeiro termo e o valor de b extraindo a raiz quadrada
de 49 no terceiro termo, portanto a = x e b = 7.
Ao substituirmos a por x e b por 7 nos termos do trinômio a2 + 2ab + b2 devemos chegar a uma variação do trinômio
original:
Realizando a substituição de a e b, vamos então analisar a2 + 2ab + b2 termo a termo para verificar se o polinômio
obtido é igual ao polinômio original.
Quando substituímos a por x em a2 chegamos ao x2 original.
Ao substituirmos a por x e b por 7 em 2ab obtivemos 2 . x . 7, equivalente ao 14x original.
E finalmente substituindo b por 7 em b2 chegamos a 72, equivalente ao 49 do terceiro termo do polinômio original.
Como foi possível escrever x2 + 14x + 49 na forma a2 + 2ab + b2, então estamos mesmo diante de um trinômio quadrado
perfeito que pode ser fatorado assim:
Portanto:
Se o polinômio em questão não fosse um trinômio quadrado perfeito, não poderíamos realizar a fatoração desta forma,
visto que a conversão de x2 + 14x + 49 em a2 + 2ab + b2 levaria a um polinômio diferente do original. Por exemplo, se o
trinômio fossex2 + 15x + 49, o segundo termo 15x iria diferir do segundo termo obtido via substituição de a e b que
é 14x, portanto não teríamos um trinômio quadrado perfeito.
Note que realizamos uma verificação termo a termo para verificar se realmente tínhamos um trinômio quadrado
perfeito, mas você não precisará fazer tal verificação quando no enunciado da questão estiver explícito que os
polinômios realmente são trinômios quadrados perfeitos.
Exemplos
Trinômio Quadrado Perfeito - Diferença: a2 - 2ab + b2 = (a - b)2
Assim como o caso da soma visto acima, de forma análoga temos o caso da diferença.
Vejamos este outro trinômio:
Como 2x é a raiz quadrada de 4x2, do primeiro termo, e 5 é a raiz quadrada de 25 do terceiro termo, podemos
reescrevê-lo como a seguir, substituindo a por 2x e b por 5 temos:
Como os respectivos termos do polinômio original e do polinômio acima são iguais, temos um trinômio quadrado
perfeito:
Portanto, temos realmente um trinômio quadrado perfeito que pode ser escrito na forma a2 - 2ab + b2 = (a - b)2:
Logo:
Exemplos
Trinômio do Segundo Grau – tipo: x² + S.x + P
A fatoração do trinômio do tipo x²+ Sx + P é o 4° caso de fatoração que vem logo após o trinômio do quadrado perfeito,
pois também é utilizado quando a expressão algébrica é um trinômio.
Quando é necessário fatorar uma expressão algébrica e essa é um trinômio (três monômios), e verificamos que esse não
forma um trinômio do quadrado perfeito, devemos então utilizar a fatoração do tipo x² + Sx + P.
Exemplo
x² – 13x + 42, para fatorarmos essa expressão algébrica devemos achar dois números que a sua soma seja igual a -13 e
seu produto igual a 42. Esses números serão -6 e -7, pois: - 6 + (- 7) = -13 e – 6 . (- 7) = 42. Portanto, a fatoração ficará
igual a: (x – 6).(x – 7).
Diferença de Dois Quadrados: a2 - b2 = (a + b)(a - b)
Este os próximos quatro tipos de fatoração que veremos estão relacionados aos produtos notáveis. Aos estudá-los
vimos que o produto da soma pela diferença de dois termos nos leva à diferença de dois quadrados, então podemos
utilizar de forma inversa este conhecimento na fatoração da diferença de dois quadrados.
Vejamos este exemplo na sequência:
Visto que a2 - b2 = (a + b)(a - b), podemos realizar a fatoração como a seguir:
Tal fatoração foi realizada se encontrando o valor de a e b, que são respectivamente a raiz quadrada do primeiro e do
segundo termo e então os substituindo em (a + b)(a - b).
Logo:
Exemplos