Ánalise de Circuitos

Ánalise de Circuitos
1. Método Intuitivo
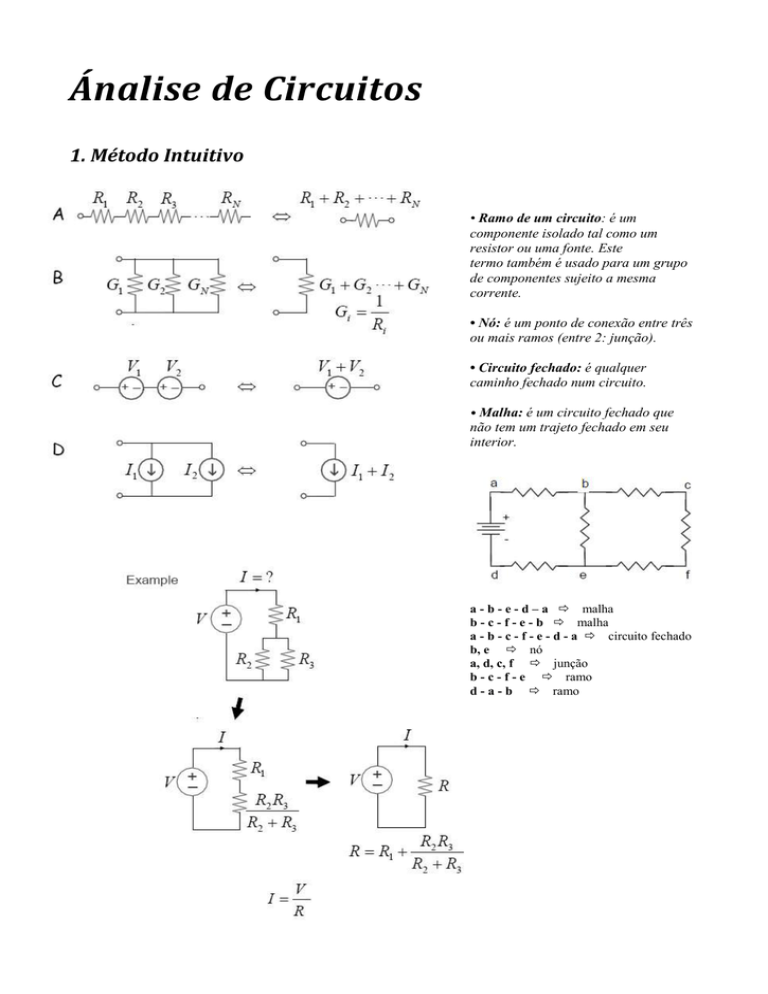
• Ramo de um circuito: é um
componente isolado tal como um
resistor ou uma fonte. Este
termo também é usado para um grupo
de componentes sujeito a mesma
corrente.
• Nó: é um ponto de conexão entre três
ou mais ramos (entre 2: junção).
• Circuito fechado: é qualquer
caminho fechado num circuito.
• Malha: é um circuito fechado que
não tem um trajeto fechado em seu
interior.
a - b - e - d – a malha
b - c - f - e - b malha
a - b - c - f - e - d - a circuito fechado
b, e nó
a, d, c, f junção
b - c - f - e ramo
d - a - b ramo
2. LCK e LTK
2.1 1ª Lei de Kirchhoff (Lei das Correntes)
Em um nó, a soma das correntes elétricas que entram é igual à soma
das correntes que saem.
, sendo a corrente elétrica
.
Convenção: todas as tensões
que estão no sentido da
corrente são positivas.
Convenção: As correntes que
entram em um nó são
consideradas como sendo
positivas e as que saem são
consideradas como sendo
negativas.
2.2 2ª Lei de Kirchhoff (Lei das Tensões)
A soma algébrica da d.d.p (Diferença de Potencial Elétrico) em um percurso fechado é
nula. Ou seja, a soma de todas as tensões (forças electromotrizes) no sentido horário é
igual à soma de todas as tensões no sentido anti-horário, ocorridas numa malha, é igual
a zero.
Logo a condutância total de resistores ligados em paralelo é igual a soma das
condutâncias individuais. Se for interessante trabalhar com resistências tem-se:
 Fonte de tensão: Abre o circuito
 Fonte te corrente: Faz um curto
2.3 Aplicação
2.3.1 Ligações Série-Paralelo
2.3.2 Divisor de corrente
2.3.3 Divisor de tensão
3. Análise Nodal
Exemplo:
1 Nó de Referência
Seleciona-se um nó como referência. O
potencial nesse nó será assumido como
zero, motivo pelo qual ele também é
chamado como nó de terra.
Dica: Usar o nó com o maior número
de elementos ligados a ele, e onde as
fontes de tensão estão conectadas.
Em seguida, nomeia-se as tensões nos
demais nós, em relação ao nó de
referência. (incógnitas primárias)
Dica: Por conveniência, usa-se:
(como impedância).
2 Aplicação da LCK aos nós
Aplica-se a LCK em todos os nós exceto no
Passo 1: escolhido o nó de referência (V=0).
nó de referência. Terá N-1 equações.
Passo 2: nomeadas as tensões e1 e e2 . (Vo é igual Vo da fonte)
Passo 3: LCK em e1 e e2:
Para se obter as tensões no resistor:
Em e1 assume-se que não entra corrente nenhuma, por isso
todos os sinais são positivos.
3 Encontrar as tensões nos nós
Em e2, Existem 3 corrente saindo (sinal positivo) e uma
entrando – da fonte (sinal negativo)
4 Voltar e encontrar tensões e
correntes dos ramos
(incógnitas secundárias)
Passo 4: Organizar as equações e resolve-las isolando as
variáveis, e depois substituindo.
3.2 Análise Nodal com Fonte de Tensão (Supernó)
Considerando que a fonte de tensão está conectada entre os terminais x e y conforme a
Figura 4 observa-se que a corrente da fonte aparecerá nas equações de ambos os nós do circuito onde a
fonte está conectada. Como não há uma relação entre a corrente da fonte e a sua tensão pode-se manter a
corrente ik da fonte como uma incógnita a ser determinada.
Por outro lado, as tensões dos nós x e y estão relacionados da seguinte forma:
Caso a fonte de tensão estiver conectada entre o nó x e o nó de terra, significa que a tensão do nó está
imposta, podendo-se neste caso desconsiderar a equação deste nó estabelecer o seguinte valor para a
tensão do nó:
O procedimento delineado corresponde ao tratamento dos dois nós onde a fonte está conectada por como
se fossem um único nó e aplicando-se a LCK para este nó composto, também chamado de super-nó.
O exemplo mostrado na Figura 5 ilustra o
procedimento. Para este circuito as equações
de nós são as seguintes:
A equação adicional considerando a
fonte de tensão é:
Substituindo as relações (31) a (34) obtém-se finalmente as equações do circuito. Deve-se notar que a
corrente da fonte de tensão aparece como uma incógnita a mais, havendo também uma equação a mais
(equação (34)).
Multiplicando-se a última equação por (-1), resulta:
As equações (34), (35) e (36) são portanto as equações básicas do circuito, sendo as incógnitas v1, v2 e If .
3.3 Teorema de Thevenin
O teorema de Thévenin afirma que, do ponto de vista de um qualquer par de terminais, um circuito linear
pode sempre ser substituído por uma fonte de tensão com resistência interna. Como se verifica na Figura
1.1, quando o objetivo da análise de um circuito se resume a identificar a corrente, a tensão ou a potência a
jusante de um par de terminais, então o teorema de Thévenin indica que todo o circuito a montante pode
ser reduzido a dois elementos apenas, constituindo globalmente uma fonte de tensão com resistência
interna. O conjunto de componentes vTh e RTh é designado por equivalente de Thévenin do circuito.
O equivalente de Thévenin calcula-se nos seguintes dois passos (para além da identificação dos terminais e
do sentido relativamente ao qual se pretende obter o equivalente):
(i) obtenção da tensão em aberto (Figura 1.2.b),
(ii) e determinação da
resistência equivalente vista
dos terminais de saída,
quando se anulam todas as
fontes independentes no
circuito.