2a Lista de Exercícios

2ª LISTA DE EXERCÍCIOS – 1º SEMESTRE DE 2015
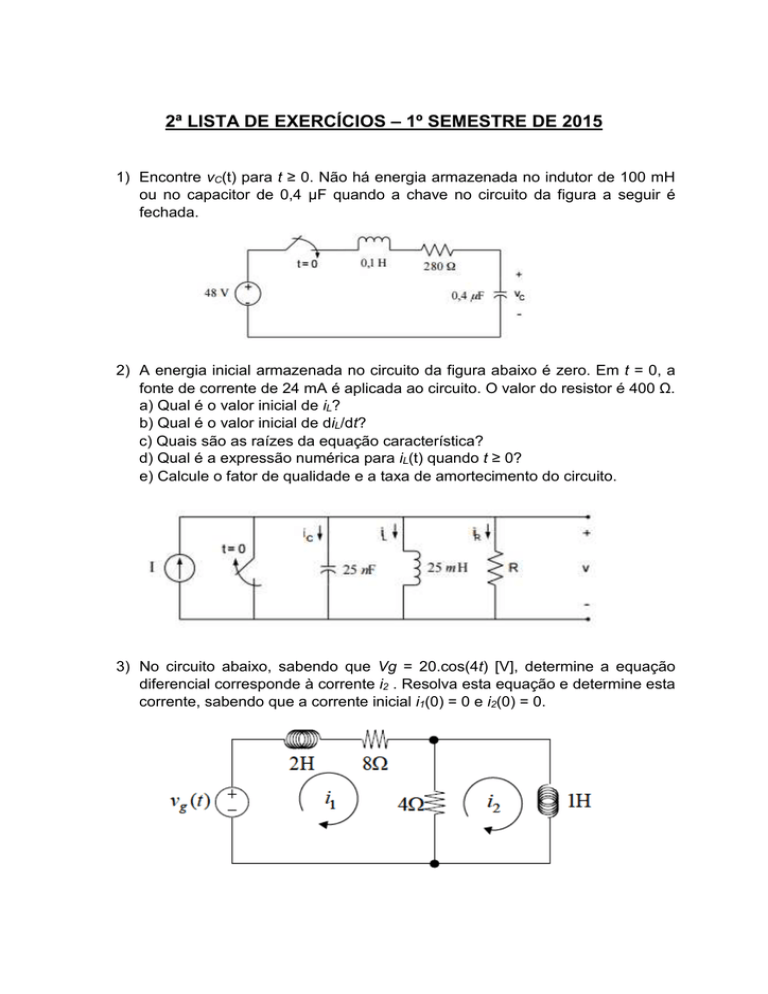
1) Encontre vC(t) para t ≥ 0. Não há energia armazenada no indutor de 100 mH
ou no capacitor de 0,4 µF quando a chave no circuito da figura a seguir é
fechada.
2) A energia inicial armazenada no circuito da figura abaixo é zero. Em t = 0, a
fonte de corrente de 24 mA é aplicada ao circuito. O valor do resistor é 400 Ω.
a) Qual é o valor inicial de iL?
b) Qual é o valor inicial de diL/dt?
c) Quais são as raízes da equação característica?
d) Qual é a expressão numérica para iL(t) quando t ≥ 0?
e) Calcule o fator de qualidade e a taxa de amortecimento do circuito.
3) No circuito abaixo, sabendo que Vg = 20.cos(4t) [V], determine a equação
diferencial corresponde à corrente i2 . Resolva esta equação e determine esta
corrente, sabendo que a corrente inicial i1(0) = 0 e i2(0) = 0.
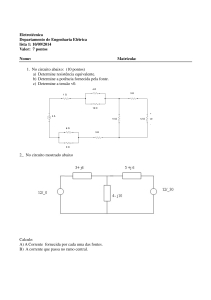
4) Um gerador de 100 V eficazes e 60 Hz alimenta o seguinte conjunto de cargas:
1- Um motor de indução de 1,5 kVA e 1,2 kW.
2- Dez lâmpadas fluorescentes de 60 W cada uma, cos θ = 0,6 em atraso.
Determine:
a) As potências ativa, reativa e aparente fornecidas pelo gerador.
b) O fator de potência da instalação, isto é, do conjunto de cargas.
c) Um bipolo (e tipo) que conectado em paralelo corrige o fator de potência
para a unidade
d) Qual é a redução porcentual da corrente fornecida pelo gerador após a
correção do fator de potência?
5) Um gerador de 100 V eficazes e 60 Hz alimenta as seguintes cargas em
paralelo:
1- Dez lâmpadas fluorescentes de 60 W cada uma, θ cos = 0,6 em atraso.
2- Uma carga de impedância Z = (6 + 12 j)Ω .
3- Um motor de indução de 1,2 kW e 2 kVA.
Determine:
a) As potências ativa, reativa e aparente fornecidas pelo gerador.
b) O fator de potência da instalação elétrica (isto é, do conjunto de cargas).
6) Considere o circuito abaixo, cuja tensão no capacitor no instante t=0 é igual a
2V e a corrente no indutor nesse mesmo instante é igual à 3A. Calcule a tensão
v(t), para is(t)=I.u(t), adotando os valores numéricos a seguir. Para cada caso
diga o tipo de amortecimento.
a) C = 0,5F, L = 2H, R = 4Ω e I = 4A;
b) C = 0,5F, L = 2H, R = 8Ω e I = 4A;
c) C = 0,5F, L = 2H, R = 2Ω e I = 4A;
7) No circuito abaixo, a chave, que estava há muito tempo na posição 1, muda
bruscamente para a posição 2, estando o capacitor inicialmente descarregado.
Determine:
a. A função v(t)
b. A soma das energias armazenadas em L e C.
8) No circuito da figura abaixo:
a. Escreva as equações de malha
b. Calcule o fasor Ê em módulo e fase
9) Dado o circuito abaixo, em regime permanente senoidal:
a. Escreva as equações nodais
b. Calcule i(t) para ω =100 rad/s
10) Fazendo uso do princípio de superposição de efeitos, determine para o circuito
abaixo:
a. O fasor VL1 da tensão no indutor que ocorre devido somente ao gerador
es1(t)
b. O fasor VL1 da tensão no indutor que ocorre devido somente ao gerador
es2(t)
c. A tensão vL(t) devida à ação simultânea dos dois geradores
11) Escreva as equações de estado para o circuito a seguir. Obtenha a expressão
para a tensão y (saída) como função algébrica das variáveis de estado e da
fonte e(t) (entrada).
12) Escreva as equações de estado para o circuito a seguir. Obtenha a expressão
para a tensão y (saída) como função algébrica das variáveis de estado e da
fonte e(t) (entrada).
13) A tensão nos terminais das cargas A, B e C é de 2300 V. As três cargas são
descritas como segue:
A: 10 kW e fator de potência de 0,707 atrasado.
B: 10 kVA e fator de potência de 0,9 adiantado.
C: 18 kW e fator de potência de 0,6 atrasado.
Se Z1=Z2=(4+2j) Ω, determine a tensão, a corrente, o fator de potência e a
potência fornecida pela fonte.
14) Calcule v1 e v2 para t>0, se o circuito está em regime permanente em t=0-.
15) Calcule o valor de v em regime permanente.
16) Calcule o fator de potência visto pelos terminais da fonte do circuito abaixo e a
reatância necessária a ser conectada em paralelo com a fonte para mudar o
fator de potência para a unidade.