Eletrodinâmica – resumo

Resumo de Eletrodinâmica
i = Corrente Elétrica (A)
Δq = quantidade de carga elétrica no fio em movimento (C = coulomb)
milicoulomb:
microcoulomb:
nanocoulomb:
n = número de elétrons
e = carga elementar de um elétron = 1,6 10-19C
Esta fórmula é usada para a
corrente elétrica média ou
quando a corrente elétrica for
constante:
i = intensidade de corrente
elétrica (A = ampère)
Δt = tempo (s = segundos)
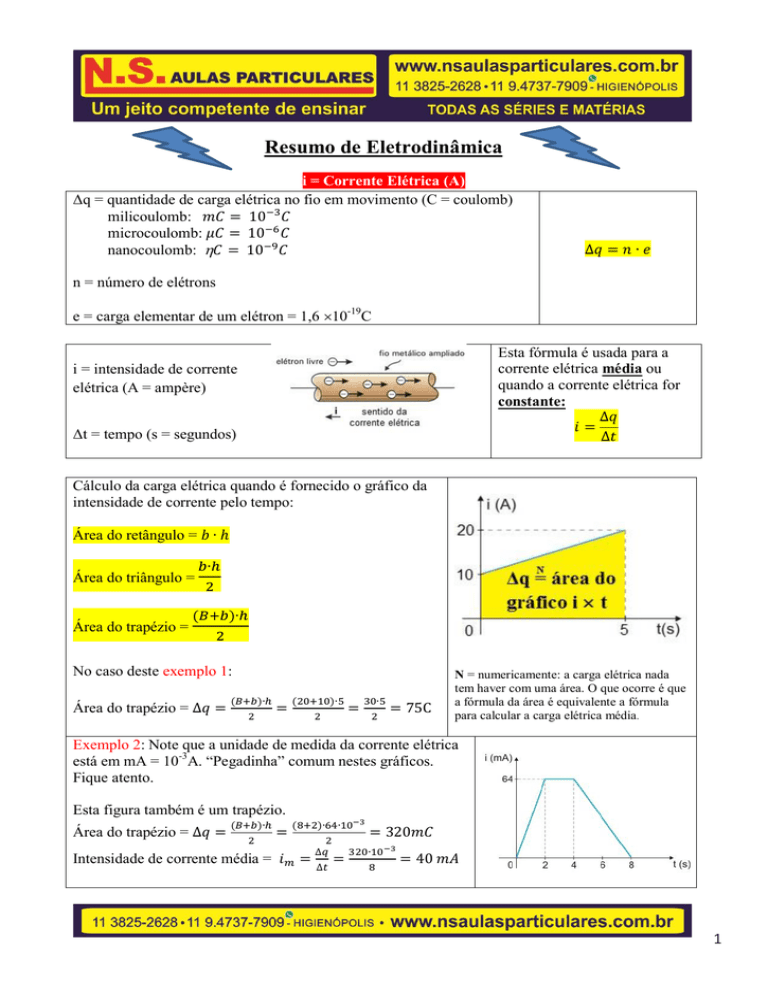
Cálculo da carga elétrica quando é fornecido o gráfico da
intensidade de corrente pelo tempo:
Área do retângulo =
Área do triângulo =
Área do trapézio =
No caso deste exemplo 1:
Área do trapézio =
N = numericamente: a carga elétrica nada
tem haver com uma área. O que ocorre é que
a fórmula da área é equivalente a fórmula
para calcular a carga elétrica média.
Exemplo 2: Note que a unidade de medida da corrente elétrica
está em mA = 10-3A. “Pegadinha” comum nestes gráficos.
Fique atento.
Esta figura também é um trapézio.
Área do trapézio =
Intensidade de corrente média =
1
U = DDP = diferença de potencial ou tensão elétrica ou voltagem (V)
U = diferença entre os potenciais de dois pontos (V = volt)
UAB = VA - VB
Exemplo 3 - tomadas:
Exemplo 4 – ligação da fiação elétrica em uma casa:
2
R = Resistência elétrica de um fio ()
Símbolos do resistor:
R = valor da resistência elétrica de um resistor ( = ohm)
ou
Resistor é um “fio fininho” que serve para limitar a
quantidade de corrente elétrica que atravessa um fio. Além
disto ele pode gerar calor e se o fio fino ou filamento ficar
em brasa irá gerar luz.
Aparelhos que usam resistores:
Nem só o “fio fininho” faz a função de um resistor. Todo
material condutor de eletricidade pode fazer esta função de
resistir a passagem de elétrons. O corpo humano e a água
salgada são bons exemplos de outros condutores.
3
1ª Lei de Ohm
U = DDP (diferença de potencial) ou tensão elétrica ou voltagem (V = volt)
1kV = 1000V
1k = 1000
1mA = 0,001A
R = resistência elétrica de um resistor ( = ohm)
i = intensidade de corrente elétrica (A = ampère)
Gráfico de resistor
ôhmico: o valor da
resistência é constante.
Gráfico de resistor não
ôhmico: o valor da
resistência é variável.
Exemplo 5:
U=R·i  5 = R·0,05
 (cte)
Exemplo 6:
U=R·i  2 = R·10

2ª Lei de Ohm
R = resistência elétrica de um resistor ( = ohm)
 = resistividade = depende do tipo de material (·m; ·cm/mm2; etc)
L = comprimento do fio (m; cm; mm; etc)
A = área da secção transversal do fio (m2; cm2; mm2; etc)
d = diâmetro da secção transversal
r = raio da secção transversal
Variação da resistência com a temperatura
R = resistência elétrica final de um resistor ( = ohm)
Ro = resistência elétrica inicial de um resistor ( = ohm)
 = coeficiente de temperatura do material (ºC-1)
Para metais  > 0 (positivo)
Para as ligas especiais  = 0 (não altera o valor da resistência)
Para a grafita e as soluções eletrolíticas  < 0 (negativo)
Δ = variação de temperatura = final - inicial
 = resistividade (·m; ·cm/mm ; etc)
2
o = resistividade inicial (·m; ·cm/mm ; etc)
2
4
Pot = Potência Elétrica (W)
Pot = potência elétrica (W = watt)
À partir da 1ª Lei de Ohm,
nas fórmulas auxiliares:
Fórmula principal:
, chegamos
e
Eel = Energia Elétrica (J ou kWh)
Eel = energia elétrica
(J = joule = para S.I. Sistema Internacional de
Unidades de Medidas)
(kWh = quilowatt-hora = para cálculo do valor
da conta de luz)
Δt = tempo
(s = segundos = para S.I.)
(h = horas = para conta de luz)

J
kWh

W
kW

s  S.I.
h  conta de luz
1 kW = 1000 W
1 h = 60 min = 3600 s
Eel = Q = Energia Elétrica transformada em térmica (J ou cal)
Eel = energia elétrica (J ou cal)
Q = quantidade de calor = energia térmica
(J ou cal)
Quando varia a temperatura:
QS = quantidade de calor sensível, usado quando
varia a temperatura mas sem mudar o estado físico.
Quando varia o estado físico:
QL = quantidade de calor latente, usado quando
muda o estado físico, mas sem variar a temperatura.
1 cal  4,2 J
1 kg = 1.000 g
m = massa (g ou kg)
cágua = 1 cal/g·ºC ou 4.200 J/kg·ºC
c = calor específico (cal/g·ºC ou J/kg·ºC)
cgelo = cvapor = 0,5 cal/g·ºC ou 2.100 J/kg·ºC
L = calor latente (cal/g ou J/kg)
Δ = variação da temperatura = final - inicial (ºC)
Lfusão do gelo = 80 cal/g ou 336.000 J/kg
Lebulição da água = 540 cal/g ou 2.268.000 J/kg
5
Associação de resistores
SÉRIE
Características:
- A corrente elétrica não se divide.
- Não existem nós (emenda de 3 ou mais fios).
- O valor da resistência elétrica total aumenta.
PARALELO
Características:
- A corrente elétrica se divide.
- Existem nós (emenda de 3 ou mais fios).
- O valor da resistência elétrica total diminui.
Req = RT = RAB = resistência equivalente ou
resistência total ()
iT = intensidade de corrente elétrica total (A)
UT = UAB = DDP ou tensão total (V)
RT = R1 + R2 + R3 + ··· + RN
iT = i1 = i2 = i3 = ··· = iN
iT = i1 + i2 + i3 + ··· + iN
UT = U1 + U2 + U3 + ··· + UN
UT = U1 = U2 = U3 = ··· = UN
Dica: Repare que nesta associação do tipo
“sériiiiiiiiii...” o valor do “i” é sempre igual.
Dica: Repare que nesta associação do tipo
“paraleluuuu...” o valor do “u” é sempre igual.
Regras práticas de cálculo para dois casos particulares de associação em paralelo
Para dois resistores (e apenas dois) em paralelo: Para N resistores iguais e em paralelo:
(produto pela soma)
6
Exemplos de exercícios de associação de resistores:
Exemplo 7 – No circuito abaixo, após fechar a
Exemplo 8 - No circuito abaixo, após fechar a
chave S, calcule:
chave S, calcule:
a) O valor da resistência total.
b) A intensidade de corrente elétrica em cada
resistor.
c) A ddp de cada lâmpada.
d) A potência de cada resistor e a potência total.
a) O valor da resistência total.
b) A intensidade de corrente elétrica em cada
resistor.
c) A ddp de cada lâmpada.
d) A potência de cada resistor e a potência total.
Exemplo 9 - No circuito abaixo, calcule:
Exemplo 10 - No circuito abaixo, calcule:
a) O valor da resistência total.
b) A ddp total e de cada resistor.
c) A intensidade de corrente elétrica em cada
resistor.
d) A potência de cada resistor e a potência total.
a) O valor da resistência total.
b) A ddp de cada resistor.
c) A intensidade de corrente elétrica total e em
cada resistor.
d) A potência de cada resistor e a potência total.
Dado: 1 k = 1.000
Exemplo 11 - No circuito abaixo UAB = 120V,
calcule:
Exemplo 12 - No circuito abaixo UAB = 70V,
calcule:
a) O valor da resistência total.
b) A ddp de cada resistor.
c) A intensidade de corrente elétrica total e em
cada resistor.
d) A potência de cada resistor e a potência total.
a) O valor da resistência total.
b) A ddp de cada resistor.
c) A intensidade de corrente elétrica total e em
cada resistor.
d) A potência de cada resistor e a potência total.
7
Exemplo 13 - No circuito abaixo UAB = 70V,
calcule:
Exemplo 14 - No circuito abaixo UAB = 70V,
calcule:
a) O valor da resistência equivalente entre os
pontos A e B.
b) A intensidade de corrente elétrica total.
c) A ddp e a corrente de cada resistor.
d) A potência total.
a) O valor da resistência equivalente entre os
pontos A e B.
b) A intensidade de corrente elétrica total.
c) A ddp e a corrente de cada resistor.
d) A potência total.
Exemplo 15 - No circuito abaixo, calcule:
Exemplo 16 - No circuito abaixo calcule o valor
da resistência equivalente entre os pontos A e B.
a) O valor da intensidade da corrente elétrica e a
ddp sobre o resistor 3.
b) O valor da ddp e o valor dos resistores 1 e 2.
c) O valor da ddp total.
d) O valor da resistência equivalente.
Exemplo 17 - No circuito abaixo calcule o valor da resistência equivalente e a intensidade da
corrente elétrica total.
Respostas:
8
Aparelhos de medidas elétricas: Amperímetro e Voltímetro
Amperímetro = aparelho que serve para medir Voltímetro = aparelho que serve para medir a
a intensidade de corrente elétrica.
ddp ou tensão elétrica ou voltagem.
É sempre colocado em série no circuito, pois em É sempre colocado em paralelo no circuito, pois
“sériiiiiiiiiii...” o valor de “i” é igual.
em “paraleluuuuuuu...” o valor do “U” é sempre
igual.
Atenção: se colocar um amperímetro em
paralelo, como sua resistência interna é muito
pequena, tendendo a zero, ela causará um
curto-circuito.
Amperímetro com voltímetro:
Atenção: se colocar um voltímetro em série,
como sua resistência interna é muito grande,
tendendo ao infinito, ele não permitirá a
passagem de corrente elétrica. O circuito apenas
para de funcionar.
Circuito com amperímetro e voltímetro
Exemplo 18 – No circuito da figura, o
Exemplo 19 – No circuito da figura abaixo, a
voltímetro indica o valor de 120V e o
bateria tem uma ddp total de 12V. Determine:
amperímetro de 4ª. Determine:
a) O valor da resistência elétrica do resistor R5.
b) O valor da intensidade da corrente elétrica
que passa pelo resistor R6.
c) O valor da DDP da bateria que o circuito está
ligado.
d) A energia consumida pelo circuito em 1
minuto.
a) A resistência elétrica total do circuito.
b) As leituras do voltímetro e do amperímetro.
c) A ddp e a intensidade de corrente elétrica no
resistor entre os pontos X e Y.
Respostas:
9
Ponte de Wheatstone
A Ponte de Wheatstone serve para descobrir o valor de um resistor desconhecido, tendo 3 resistores
conhecidos e um galvanômetro ou um fio de comprimento conhecido e um galvanômetro.
O Galvanômetro é um medidor de corrente elétrica de baixa intensidade. Para valer as relações
matemática, a condição é que o valor marcado no galvanômetro seja de zero ampères.
A relação matemática para esta Ponte de
Wheatstone é obtida ao se igualar a
multiplicação dos resistores que estão nas
diagonais opostas.
A relação matemática para a Ponte de
Wheatstone com fios é obtida igualando as
multiplicações dos resistores com os
comprimentos dos fios que estão nas diagonais
opostas.
Exemplo 20 – O galvanômetro da figura abaixo indica zero ampères.
Isto significa que a Ponte de Wheatstone esá em equilíbrio e é possível
aplicar a sua relação matemática.
Determine:
a) O valor do resistor R.
b) A intensidade de corrente elétrica no resistor de 15.
c) A ddp no resistor de 20.
d) A corrente elétrica total do circuito.
Resposta:
10
Gerador
Gerador é o elemento que fornece a ddp e corrente elétrica para o circuito.
Pode ser uma pilha, uma bateria ou uma tomada que transmite a energia do gerador de uma usina
hidrelétrica.
Gerador de corrente contínua
Gerador de corrente alternada
As pilhas ou baterias fornecem uma corrente
contínua, ou seja, a corrente elétrica tem um
único sentido.
A tomada fornece uma corrente alternada, ou seja, a
corrente elétrica muda de sentido várias vezes por
segundo. No Brasil, esta frequência é de 60Hz, ou
seja, a corrente inverte de sentido 60 vezes em um
segundo.
Receptor
Receptor é o elemento que absorve a energia gerada por um gerador.
Pode ser um motor ou uma pilha invertida no circuito.
Um receptor só funciona se estiver ligado a um gerador, necessariamente.
11
Equações de Gerador e Receptor
Gerador:
A corrente elétrica entra pelo – e sai pelo +
A ddp útil nos terminais do gerador (U) é o
resultado de toda ddp gerada (E) pela fem
menos o que o próprio gerador gastou com sua
resistência interna (Uresistência = r·i).
Receptor:
A corrente elétrica entra pelo + e sai pelo –
A ddp total nos terminais do receptor (U`) é o
resultado da ddp útil pela fcem (E`) mais o que o
próprio receptor gastou com sua resistência
interna (U`resistência = r`·i).
Uútil gerado = Utotal do gerador - Udissipado pelo resistor
U = E – r·i
Utotal gasto = Uútil do receptor + Udissipado pelo resistor
U = ddp útil (diferença de potencial) (V)
E = fem = força eletro motriz = ddp total gerada
pela bateria (V)
r = resistência interna do gerador ()
R = resistência externa ao gerador ()
i = corrente elétrica do circuito (A)
U` = E` + r`·i
U` = ddp total (diferença de potencial) (V)
E` = fcem = força contra eletro motriz = ddp útil
gasta pelo receptor (V)
r` = resistência interna do receptor ()
Para o circuito externo, a ddp útil do gerador é a
mesma consumida pelo resistor externo, assim:
Uma vez que a ddp útil do gerador é a mesma
para o receptor mais o resistor, podemos igualar:
U = Ri
U`receptor + Uresistor = Ugerador 
E` + r`i + Ri = E - ri  r`·i +Ri + ri = E – E`
Uma vez que a ddp útil é a mesma para o
gerador e para o circuito externo (resistor),
podemos igualar:
U = U  Ri = E - ri  Ri + ri = E
Lei de Pouillet:
Lei de Pouillet:
Onde:
, ou seja, a ddp gerada tem que ser
maior que a ddp consumida ou recebida.
12
Associação de geradores e receptores
Para vários geradores e receptores associados
em série:
Gerador
Lei de Pouillet:
Sempre é uma função do 1º grau
decrescente.
Os valores de E e r são constantes.
∑
∑
∑
∑ , ou seja, a ddp total gerada
Onde: ∑
tem que ser maior que a ddp total consumida ou
recebida.
Gráficos de Gerador, Receptor e Resistor
Receptor
U = E - r·i
∑
∑
U` = E` + r`·i
Sempre é uma função do 1º
grau crescente.
Os valores de E` e r` são
constantes.
Exemplo 21 - U = 36 - 3·i, ou seja, E =
Exemplo 22 - U = 9 + 3·i, ou
36V e r = 3.
seja, E` = 36V e r` = 3.
Resistor
U = Ri
Sempre é uma função do
1º grau crescente que tem
início na origem do
sistema de coordenadas
cartesianas.
O valor de R é constante.
Exemplo 23 - U = 3·i, ou
seja, R = 5.
Observação:
- Quando i = 0, o valor de U é a
própria fem E. Isto significa que os
terminais do gerador estão abertos ou
desconectados.
- Quando o valor de E = 0, o valor de i
é icc = E/r. Chamamos este i de icc, ou
seja, corrente de curto circuito. Ocorre
quando os terminais do gerador estão
ligados diretamente em curto-circuito.
13
Potência de Gerador e Receptor (W)
Gerador
Receptor
Pt = Pu + Pd
Pt = Pu + Pd
Pt = Potência gerada ou potência total
Pt = E·i
Pt = Potência consumida ou potência total
Pt = U`·i
Pu = Potência útil ou potência a ser utilizada fora
do gerador ou potência dissipada pelo resistor
externo ao gerador.
Pu = U·i = R·i2
Pu = Potência útil ou potência a ser utilizada
pelo motor em funcionamento. Transforma a
energia elétrica em cinética pelo magnetismo
Pu = E`·i
Pd = Potência dissipada na forma de calor pela
própria resistência interna do gerador.
Pd = r·i2
Pd = Potência dissipada na forma de calor pela
própria resistência interna do receptor.
Geralmente os fios do enrolamento do motor
geram esta resistência.
Pd = r`·i2
Potência Útil Máxima do Gerador (W)
Ocorre quando o valor da corrente elétrica vale
metade da corrente de curto-circuito. Assim:
( )
 equação do 2º grau  parábola 
(
)
Rendimento do Gerador e Receptor(
Gerador
)
Receptor
14
Leis de Kirchhoff
Lei dos Nós
Lei das Malhas
A somatória das correntes elétricas que chegam
em um nó são iguais a somatória das correntes
elétricas que saem dos nós.
∑
A somatória de todas as ddps em uma malha é
sempre igual a zero.
Lembrando: U=R·i
∑
∑
∑
∑
Sentido da ddp para ser considerado em cada aparelho:
Gerador: o sentido da ddp é
sempre do – para o +
Receptor: o sentido da ddp é
sempre do – para o +
Resistor: o sentido da ddp é
sempre opôs ao da corrente
elétrica.
Exemplo 24 – Dado o circuito abaixo, determine:
a) Os valores de i1, i2 e i3.
b) A ddp entre os pontos AB, AC, AD e AE.
Respostas:
15
RESUMÃO
Associação de resistores em
sériiiiiiiiiii... (o “i” é igual):
RT = R1 + R2 + R3 + ··· + RN
Carga elétrica (C):
Corrente elétrica (A):
Gerador:
U = E – r·i
U = Ri
iT = i1 = i2 = i3 = ··· = iN
Δq = área do gráfico i x t
UT = U1 + U2 + U3 + ··· + UN
Associação de resistors em
paraleluuuu… (o “U” é igual):
DDP (V):
UAB = VA - VB
1ª Lei de Ohm:
iT = i1 + i2 + i3 + ··· + iN
2ª Lei de Ohm ():
UT = U1 = U2 = U3 = ··· = UN
Para dois resistores em
paralelo:
Pt = Pu + Pd; Pt = E·i
Pu = U·i = R·i2; Pd = r·i2
Para N resistores iguais em
paralelo:
Receptor:
U` = E` + r`·i
Ponte de Wheatstone:
Variação da resistência elétrica
com a temperatura:
ou
Leis de Kirchhoff:
Potência elétrica (W):
;
∑
ou
Energia elétrica (J ou kWh):
Energia elétrica transformada
em térmica (quantidade de
calor) (J ou cal):
ou
ou
∑
∑
∑
∑
Pt = Pu + Pd; Pt = U`·i
Pu = E`·i; Pd = r`·i2
Associação de geradores com
receptores:
∑
∑
∑
∑
∑
By Prof. Nilton Sihel – imagem obtidas na internet e adaptada para esta apostila
16