MUV – Movimento Uniformemente Variado

MUV – Movimento Uniformemente Variado
1. (Uece 2015) Um carro, partindo do repouso, desloca-se em um trecho A de modo que sua velocidade
aumente linearmente com o tempo até atingir 60km h. Após algum tempo, em um trecho B, o motorista
aciona o freio, de modo que a velocidade decresça também linearmente com o tempo. Considere que a
trajetória do automóvel é retilínea nos dois trechos e que ambos sejam estradas sem aclives ou declives.
Assim, pode-se afirmar corretamente que o vetor aceleração nos dois trechos tem
a) mesma direção e mesmo sentido.
b) mesma direção e sentido contrário.
c) mesmo módulo e mesmo sentido.
d) direções perpendiculares e mesmo módulo.
2. (Upe 2015) Duas partículas, 1 e 2, se movem ao longo de uma linha horizontal, em rota de encontro com
velocidades iniciais de módulos iguais a v1  10m / s e v2  14m / s e acelerações contrárias às suas
velocidades de módulos a1  1,0m / s2 e a2  0,5m / s2 .
Sabendo que o encontro entre elas ocorre, apenas, uma vez, o valor da separação inicial, d, entre as partículas
vale
a) 4 m
b) 8 m
c) 16 m
d) 96 m
e) 192m
3. (G1 - ifsul 2015) Dois móveis, A e B, movendo-se em um plano horizontal, percorrem trajetórias
perpendiculares, seguindo os eixos Ox e Oy, de acordo com as funções horárias x A  18  3t e
yB  18  9t  2t2 ,
com unidades de acordo com o Sistema Internacional de Unidades (S.I.).
Esses móveis irão se encontrar no instante
a) t  0,0s
b) t  3,0s
c) t  4,5s
d) t  6,0s
4. (Unicamp 2015) A Agência Espacial Brasileira está desenvolvendo um veículo lançador de satélites
(VLS) com a finalidade de colocar satélites em órbita ao redor da Terra. A agência pretende lançar o VLS em
2016, a partir do Centro de Lançamento de Alcântara, no Maranhão.
a) Considere que, durante um lançamento, o VLS percorre uma distância de 1200km em 800s. Qual é a
velocidade média do VLS nesse trecho?
b) Suponha que no primeiro estágio do lançamento o VLS suba a partir do repouso com aceleração resultante
constante de módulo aR . Considerando que o primeiro estágio dura 80s, e que o VLS percorre uma
distância de 32km, calcule aR .
5. (Ufrgs 2015) Trens MAGLEV, que têm como princípio de funcionamento a suspensão eletromagnética,
entrarão em operação comercial no Japão, nos próximos anos. Eles podem atingir velocidades superiores a
550 km / h. Considere que um trem, partindo do repouso e movendo-se sobre um trilho retilíneo, é
uniformemente acelerado durante 2,5 minutos até atingir 540km / h.
Nessas condições, a aceleração do trem, em m / s2 , é
a) 0,1.
b) 1.
c) 60.
d) 150.
e) 216.
TEXTO PARA A PRÓXIMA QUESTÃO:
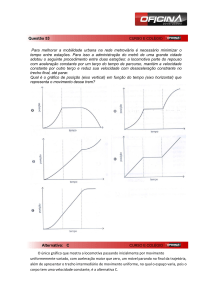
Para responder à(s) questão(ões), considere as afirmativas referentes à figura e ao texto abaixo.
Na figura acima, está representada uma pista sem atrito, em um local onde a aceleração da gravidade
é constante. Os trechos T1, T2 e T3 são retilíneos. A inclinação de T1 é maior do que a inclinação de T3, e o
trecho T2 é horizontal. Um corpo é abandonado do repouso, a partir da posição A.
6. (Pucrs 2015) Com base nessas informações, afirma-se:
I. O movimento do corpo, no trecho T1, é uniforme.
II. No trecho T3, o corpo está em movimento com aceleração diferente de zero.
III. No trecho T2, a velocidade e a aceleração do corpo têm a mesma direção e o mesmo sentido.
Está/Estão correta(s) a(s) afirmativa(s)
a) I, apenas.
b) II, apenas.
c) I e III, apenas.
d) II e III, apenas.
e) I, II e III.
7. (Unicamp 2014) Correr uma maratona requer preparo físico e determinação. A uma pessoa comum se
recomenda, para o treino de um dia, repetir 8 vezes a seguinte sequência: correr a distância de 1 km à
velocidade de 10,8 km/h e, posteriormente, andar rápido a 7,2 km/h durante dois minutos.
a) Qual será a distância total percorrida pelo atleta ao terminar o treino?
b) Para atingir a velocidade de 10,8 km/h, partindo do repouso, o atleta percorre 3 m com aceleração
constante. Calcule o módulo da aceleração a do corredor neste trecho.
8. (Uerj 2014) O cérebro humano demora cerca de 0,36 segundos para responder a um estímulo. Por
exemplo, se um motorista decide parar o carro, levará no mínimo esse tempo de resposta para acionar o freio.
Determine a distância que um carro a 100 km/h percorre durante o tempo de resposta do motorista e calcule a
aceleração média imposta ao carro se ele para totalmente em 5 segundos.
9. (Uel 2014) O desrespeito às leis de trânsito, principalmente àquelas relacionadas à velocidade permitida
nas vias públicas, levou os órgãos regulamentares a utilizarem meios eletrônicos de fiscalização: os radares
capazes de aferir a velocidade de um veículo e capturar sua imagem, comprovando a infração ao Código de
Trânsito Brasileiro.
Suponha que um motorista trafegue com seu carro à velocidade constante de 30 m/s em uma avenida cuja
velocidade regulamentar seja de 60 km/h. A uma distância de 50 m, o motorista percebe a existência de um
radar fotográfico e, bruscamente, inicia a frenagem com uma desaceleração de 5 m/s 2.
Sobre a ação do condutor, é correto afirmar que o veículo
a) não terá sua imagem capturada, pois passa pelo radar com velocidade de 50 km/h.
b) não terá sua imagem capturada, pois passa pelo radar com velocidade de 60 km/h.
c) terá sua imagem capturada, pois passa pelo radar com velocidade de 64 km/h.
d) terá sua imagem capturada, pois passa pelo radar com velocidade de 66 km/h.
e) terá sua imagem capturada, pois passa pelo radar com velocidade de 72 km/h.
10. (Ucs 2014) Tendo chegado atrasado ao casamento, um convidado conseguiu pegar uma última fatia de
bolo e concluiu que experimentara o melhor glacê de toda a sua vida. Ouvindo falar que na cozinha havia
mais um bolo, mas que seria cortado apenas em outra festa, ele foi até lá. Viu o bolo em cima de uma mesa
perto da porta. Porém, percebeu que havia também uma cozinheira de costas para o bolo e para ele. Querendo
passar o dedo no bolo sem ser pego pela cozinheira e conseguir pegar a maior quantidade de glacê possível, o
convidado deduziu que, se passasse muito rápido, o dedo pegaria pouco glacê; mas, se passasse muito
lentamente, corria o risco de ser descoberto. Supondo, então, que ele tenha 3 segundos para roubar o glacê
sem ser notado e que a melhor técnica para conseguir a maior quantidade seja passar o dedo por 40,5 cm de
bolo em MRUV, partindo do repouso, qual aceleração teria o dedo no intervalo de tempo do roubo do glacê?
a) 0,03 m / s2
b) 0,04 m / s2
c) 0,09 m / s2
d) 1,05 m / s2
e) 2 m / s2
11. (G1 - ifpe 2014) Um trem bala, viajando a 396 km / h, tem a sua frente emparelhada com o início de um
túnel de 80 m de comprimento (ver figura). Nesse exato momento, o trem desacelera a uma taxa de 5 m / s2 .
Sabendo-se que o trem mantém essa desaceleração por todo o tempo em que atravessa completamente o túnel
e que o mesmo possui 130 m de comprimento, é correto dizer que o trem irá gastar, para ultrapassá-lo
totalmente, um tempo, em segundos, igual a:
a)
b)
c)
d)
e)
3,6
2,0
6,0
1,8
2,4
12. (Pucrs 2014) Muitos acidentes acontecem nas estradas porque o motorista não consegue frear seu carro
antes de colidir com o que está à sua frente. Analisando as características técnicas, fornecidas por uma revista
especializada, encontra-se a informação de que um determinado carro consegue diminuir sua velocidade, em
média, 5,0 m / s a cada segundo. Se a velocidade inicial desse carro for 90,0 km / h (25,0 m / s), a distância
necessária para ele conseguir parar será de, aproximadamente,
a) 18,5 m
b) 25,0 m
c) 31,5 m
d) 45,0 m
e) 62,5 m
Gabarito:
Resposta da questão 1:
[B]
No trecho A, o carro parte do repouso e aumenta sua velocidade uniformemente até atingir a velocidade de
60km h.
Desta forma, a aceleração durante o trecho A tem direção como sendo a horizontal e sentido da esquerda para
a direita.
No trecho B, o carro está inicialmente com uma velocidade de 60km h e vai desacelerando até atingir o
repouso.
Assim, a aceleração no trecho B tem mesma direção que no sentido A (horizontal), porém está no sentido
contrário (da direita para a esquerda).
Resposta da questão 2:
[E]
Tomando as equações horárias das posições de cada móvel, temos:
s1  0  10t 
1 2
t
2
1
4
e s2  d  14t  t 2
Em que
S  posição de cada móvel (m) no instante t (s)
No encontro dos móveis, as posições são iguais. s1  s2
1
1
10t  t 2  d  14t  t 2
2
4
Rearranjando os termos
3t2  96t  4d  0 (1)
Sabendo que o encontro ocorre apenas uma vez, temos um choque totalmente inelástico, isto é, a velocidade
final das duas partículas é a mesma.
v1  10  t e v 2  14 
t
2
v1  v 2
10  t  14 
t
48
t
 t  16 s
2
3
Substituindo o tempo encontrado na equação (1), obtemos:
3  162  96  16  4d  0  d  192m
Outra forma de pensar a resolução desta questão a partir da equação (1) é que o encontro dos móveis significa
as raízes da equação quadrática. Como esse encontro se dá uma única vez, temos duas raízes reais iguais, ou
seja, Δ  0, então:
( 96)2  4  3  4d  0
9216  48d  0
9216
d
 d  192 m
48
Resposta da questão 3:
[D]
O encontro ocorrerá no ponto (0, 0), origem do sistema de eixos.
18

x A  18  3 t  0  18  3 t  t 
 t6 s

3


 y  18  9t  2t 2  0  18  9t  2t 2  t   9  81  144
B

4

t  6 s.
Resposta da questão 4:
a) Dados: ΔS  1.200 km  1.200  103 m; Δt  800 s.
vm 
ΔS 1.200  103


Δt
800
vm  1.500 m/s.
b) Dados: S  32 km  32.000 m; S0  0; v0  0; t  80 s.
S  S0  v 0 t 
aR 2
aR
t  32.000 
802 
2
2
a R  10 m/s2 .
Resposta da questão 5:
[B]
Dados : v  540 km/h  150 m/s; Δt  2,5 min  150 s.
a
Δ v 150  0


Δt
150
a  1 m/s2 .
t  1,5 s
t6s

Resposta da questão 6:
[B]
[I] Incorreta. O movimento do corpo no trecho T1 é acelerado.
[II] Correta. No trecho T3, o corpo está em movimento com aceleração diferente de zero, em sentido oposto
ao da velocidade, pois o movimento é retardado.
[III] Incorreta. No trecho T2, a velocidade é constante e a aceleração é nula.
Resposta da questão 7:
a) Dados: d1 = 1 km = 1.000 m; v2 = 7,2 km/h = 2 m/s; Δt2  2min  120s.
A distância total (d) percorrida nas 8 vezes é:


d  8  d1  d2   8 d1  v 2 Δt 2  8 1.000  2  120   8 1.240  
d  9.920 m.
b) Dados: v0 = 0; v1 = 10,8 km/h = 3 m/s; ΔS  3m.
Aplicando a equação de Torricelli:
v12  v 02  2 a ΔS  a 
v12  v 02 32  0 9


2 Δs
23
6

a  1,5 m/s2 .
Resposta da questão 8:
 Distância percorrida durante o tempo de resposta:
Dados: v = 100 km/h = (100/3,6) m/s; Δt  0,36s.
D  v Δt 
100
 0,36  D  10 m.
3,6
 Aceleração média de frenagem:
Dados: v0 = 100 km/h = (100/3,6) m/s; v = 0; Δt  5s.
Supondo trajetória retilínea, a aceleração escalar é:
a
100
Δv 0 
3,6

 a  5,6 m/s2 .
Δt
5
Resposta da questão 9:
[E]
Da equação de Torricelli:
v 2  v 02  2 a ΔS  v 2  302  2  5  50  v 2  400  v  20 m/s 
v  72 km/h.
Resposta da questão 10:
[C]
Dados: ΔS  40,5cm  0,405m; v0  0; t  3s.
ΔS  v0 t 
a 2
a
0,81
t  0,405  32  a 

2
2
9
a  0,09 m/s2 .
Resposta da questão 11:
[B]
Dados: ΔS  130  80  210 m; v0  396 km/h  110 m/s; a  5 m/s2 .
Aplicando a equação horária do espaço para movimento uniformemente variado:
a 2
5
t  210  110 t  t 2  t 2  44 t  84  0 
2
2
t  2 s.
44  1936  336
t
t

t  2 s.
2
t  42 s. (não convém)
ΔS  v 0 t 
Resposta da questão 12:
[E]
A aceleração escalar é a  5 m / s2.
Aplicando a equação de Torricelli:
v 2  v 02  2 a ΔS
 0  252  2  5  ΔS  ΔS 
625
10

ΔS  62,5 m.