1. Arthur monta um circuito com duas lâmpadas idênticas e

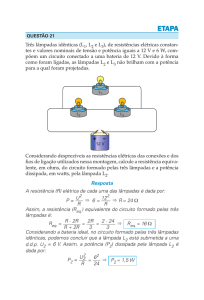
1. Arthur monta um circuito com duas lâmpadas idênticas e conectadas à mesma bateria,
como mostrado nesta figura:
Considere nula a resistência elétrica dos fios que fazem a ligação entre a bateria e as duas
lâmpadas. Nos pontos A, B, C e D, indicados na figura, as correntes elétricas têm,
respectivamente, intensidades iA , iB , iC e iD .
a) A corrente elétrica IB é menor, igual ou maior à corrente elétrica iC ? Justifique sua resposta.
b) Qual é a relação correta entre as correntes elétricas iA , iB e iD ? Justifique sua resposta.
c) O potencial elétrico no ponto A é menor, igual ou maior ao potencial elétrico no ponto C?
Justifique sua resposta.
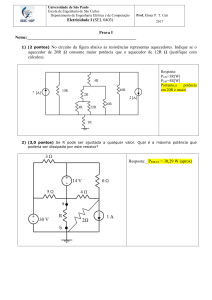
2. Um estudante montou o circuito da figura com três lâmpadas idênticas, A, B e C, e uma
bateria de 12V. As lâmpadas têm resistência de 100.
a) Calcule a corrente elétrica que atravessa cada uma das lâmpadas.
b) Calcule as potências dissipadas nas lâmpadas A e B e identifique o que acontecerá com
seus respectivos brilhos (aumenta, diminui ou permanece o mesmo) se a lâmpada C
queimar.
3. Considere o circuito elétrico que esquematiza dois modos de ligação de duas lâmpadas
elétricas iguais, com valores nominais de tensão e potência elétrica 60 V e 60 W,
respectivamente.
Modo A – ambiente totalmente iluminado: a chave Ch, ligada no ponto A, mantém as lâmpadas
L1 e L 2 acesas.
Modo B – ambiente levemente iluminado: a chave Ch, ligada no ponto B, mantém apenas a
lâmpada L1 acesa, com potência menor do que a nominal, devido ao resistor R de resistência
ôhmica constante estar ligado em série com L1 .
Considerando que as lâmpadas tenham resistência elétrica constante, que os fios tenham
resistência elétrica desprezível e que a diferença de potencial de 120 V que alimenta o circuito
seja constante, calcule a energia elétrica consumida, em kWh, quando as lâmpadas
permanecem acesas por 4 h, ligadas no modo A – ambiente totalmente iluminado. Determine a
resistência elétrica do resistor R, para que, quando ligada no modo B, a lâmpada L1 dissipe
uma potência de 15 W.
4.
A figura acima representa, de forma esquemática, a instalação elétrica de uma residência, com
circuitos de tomadas de uso geral e circuito específico para um chuveiro elétrico. Nessa
residência, os seguintes equipamentos permaneceram ligados durante 3 horas a tomadas de
uso geral, conforme o esquema da figura: um aquecedor elétrico (Aq) de 990 W, um ferro de
passar roupas de 980 W e duas lâmpadas, L1 e L2, de 60 W cada uma. Nesse período, além
desses equipamentos, um chuveiro elétrico de 4400 W, ligado ao circuito específico, como
indicado na figura, funcionou durante 12 minutos. Para essas condições, determine
a) a energia total, em kWh, consumida durante esse período de 3 horas;
b) a corrente elétrica que percorre cada um dos fios fase, no circuito primário do quadro de
distribuição, com todos os equipamentos, inclusive o chuveiro, ligados;
c) a corrente elétrica que percorre o condutor neutro, no circuito primário do quadro de
distribuição, com todos os equipamentos, inclusive o chuveiro, ligados.
NOTE E ADOTE
- A tensão entre fase e neutro é 110 V e, entre as fases, 220 V.
- Ignorar perdas dissipativas nos fios.
- O símbolo  representa o ponto de ligação entre dois fios.
TEXTO PARA A PRÓXIMA QUESTÃO:
Dados:
Aceleração da gravidade: 10 m/s2
Densidade do mercúrio: 13,6 g/cm3
Pressão atmosférica: 1,0  105 N/m2
Constante eletrostática: k0  1 40  9,0  109 N  m2 C2
5. No circuito RC, mostrado abaixo, a chave Ch está aberta. Inicialmente o capacitor está
carregado e sua ddp é VC  22 V . A chave Ch é fechada e uma corrente elétrica começa a
circular pelo circuito. Calcule a intensidade da corrente elétrica inicial que circula no resistor,
em ampères.
TEXTO PARA A PRÓXIMA QUESTÃO:
Use quando necessário:
- Aceleração da gravidade g  10m / s2 ; Densidade da água   1,0g / cm3  1000kg / m3
- Velocidade da luz no vácuo c  3,0  108 m / s
- Constante de Planck h  6,63  1034 J  s  4,14  1015 eV  s;
- Constante   3,14
6. Uma bateria de automóvel tem uma força eletromotriz   12V e resistência interna r
desconhecida. Essa bateria é necessária para garantir o funcionamento de vários componentes
elétricos embarcados no automóvel. Na figura a seguir, é mostrado o gráfico da potência útil P
em função da corrente i para essa bateria, quando ligada a um circuito elétrico externo.
a) Determine a corrente de curto-circuito da bateria e a corrente na condição de potência útil
máxima. Justifique sua resposta.
b) Calcule a resistência interna r da bateria.
c) Calcule a resistência R do circuito externo nas condições de potência máxima.
d) Sabendo que a eficiência  de uma bateria é a razão entre a diferença de potencial V
fornecida pela bateria ao circuito e a sua força eletromotriz  , calcule a eficiência da bateria
nas condições de potência máxima.
e) Faça um gráfico que representa a curva característica da bateria. Justifique sua resposta.
Gabarito:
Resposta da questão 1:
O esquema a seguir ilustra a situação:
a) Os pontos B e C estão no mesmo fio, portanto, por eles passa a mesma corrente:
iB = iC = i.
b) Como as duas lâmpadas estão em paralelo e têm resistências iguais, elas são percorridas
por correntes iguais. Então:
iB = iD = i.
Essas duas correntes, iB e iD, somam-se formando a corrente iA. Assim:
iA = iB + iD = i + i  iA = 2 i. .
Portanto, a relação correta é:
i
iB  iD  A .
2
c) A diferença de potencial elétrico entre dois pontos é U = R i. Como entre os pontos citados,
A e C, não há elemento resistivo algum, o potencial elétrico no ponto A é igual ao potencial
elétrico no ponto C.
Resposta da questão 2:
a) Dados: U = 12 V; R = 100 .
A resistência equivalente do circuito é:
100
Req  100 
 Req  150 Ω.
2
Aplicando a lei de Ohm-Pouillet:
12
URI  I
 I  0,08 A.
150
Assim:
eq
iA  I  0,08 A;


I
iB  iC   0,04 A.

2
b) Calculemos as potências dissipadas para o caso do item anterior:
P  100  0,08 2  0,64 W;
 A
2
PR i  
2

PB  PC  100  0,04   0,16 W.
Se a lâmpada C queimar, as lâmpadas A e B ficam em série, submetidas à tensão U’ = 6 V
cada uma.
As novas potências dissipadas serão:
2
U'
62
 0,36 W.
R
100
Comparando os valores obtidos, concluímos que o brilho da lâmpada A diminui e o brilho da
lâmpada B aumenta.
P
 PA'  PB' 
Resposta da questão 3:
Dados: UL = 60 V; PL = 60 W = 0,6 kW; U = 120 V.
No modo A as lâmpadas estão em série e ligadas à rede de 120 V. Portanto, elas estão
operando em condições nominais, ou seja, cada uma está sob tensão de 60 V, dissipando 60
W. A energia elétrica consumida pelas duas lâmpadas em 4 h é:
E  2 P t  2  0,06  4   E  0,48 kWh.
A resistência RL de cada lâmpada é:
RL 
UL2 60  60

PL
60
 RL  60 .
No modo B, a potência é PL' = 15 W. Para essa potência a corrente é:
PL'  RLi2  15  60 i2  i2 =
1
4
 i  0,5.
Aplicando a lei de Ohm-Poullet para o modo B:
U  R  RL  i  120  R  60  0,5  R 
120
 60  R  180 .
0,5
Resposta da questão 4:
a) A energia total consumida é o somatório das energias consumidas pelos aparelhos. Da
expressão da potência:
E
12
P
 E  P Δt  990  980  2  60  W  3h  4.400W 
h  E  7.150 Wh 
Δt
60
E  7,15 kWh.
b) A figura a seguir mostra um esquema simplificado desse circuito, representando as tomadas
como fontes de corrente contínua e todos os dispositivos como resistores.
Da expressão da potência elétrica:
P
PU i  i
U
Apliquemos essa expressão em cada dispositivo e a lei dos nós em A, B e C no circuito
primário.
4.400 990

 20  9  i1  29A.
220 110
4.400
60 980
12 98
110
Nó C: i2  iC  2iL  iF 
2

 20 

 20 
 i2  30A.
220
110 110
11 11
11
Nó A: i1  iC  iA 
c) Nó B: iN  i1  i2  iN  29  30  iN  1 A.
Resposta da questão 5:
De acordo com a segunda lei de Kirchhoff, teremos:
VC  VR  ε  0  22  VR  12  0
VR  10V
Aplicando a definição de resistência elétrica:
VR
10
2
i
i
i  5A
R
Resposta da questão 6:
a) Quando a bateria está em curto-circuito, toda potência gerada é dissipada internamente,
pois a resistência externa é nula. A corrente tem intensidade máxima (imáx) e é chamada de
corrente de curto-circuito (ic).
Do gráfico:
ic  imáx  120 A.
Também do gráfico, a potência útil máxima é 360 W, o que corresponde à corrente de 60 A.
b) Dado: ε  12 V.
A potência útil é igual à potência gerada, descontando a potência dissipada internamente.
Pu  Pg  Pd  Pu  ε i  r i2.
Essa expressão explica porque o gráfico dado é uma parábola de concavidade para baixo.
Aplicando nessa expressão a condição de potência máxima:
360
2
360  12  60   r  60 
 3.600 r  720  360  r 

3.600
r  0,1 Ω.
c) Aplicando a 1ª lei de Ohm e a equação do gerador para a condição de potência máxima (i =
60 A):
 V  ε  ri



V  R i
R  0,1 Ω.
 R i  ε r i  R 
d) Do enunciado:
V ε  r i 12  0,1 60  6 1
η 



ε
ε
12
12 2
A equação dessa bateria é:
V  ε  r i  V  12  0,1 i.
O gráfico é a reta dada abaixo.
ε r i
i
 R
 η  50%.
12  0,1 60 
60

6

60