Ementa e programa da disciplina Matemática para Zootecnia

Centro de Ciências Exatas
Departamento de Matemática
Código
6 MAT 049
Ano Letivo
2010
PLANO DE CURSO DA DISCIPLINA
Nome
MATEMÁTICA PARA ZOOTECNIA
Curso
ZOOTECNIA
T
72
1.
Carga Horária
P
Total
36
108
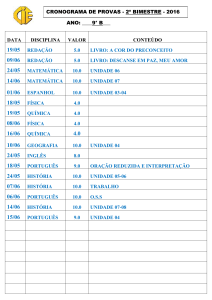
Oferta
Anual
Semestral
Série
1ª
Semestre
1º
2º
Habilitação(ões)
EMENTA
Números reais e conjuntos, funções, métodos e gráficos. Limites e continuidade de funções de
uma variável. Derivadas e suas aplicações. Integrais e suas aplicações. Matrizes e sistemas de
equações lineares. Determinantes. Espaço vetorial. Transformações lineares. Diagonalização
de operadores. Equações diferenciais de 1a. ordem e suas aplicações.
2.
OBJETIVOS
1
Estudar a matemática básica e analisar limites, derivadas, integrais, com as suas mais
diversas aplicações à Zootecnia. Estudar matrizes, sistemas lineares e equações
diferenciais, a fim de solucionar problemas relativos à Zootecnia.
3.
CONTEÚDO PROGRAMÁTICO E CRONOGRAMA
1.
Números Reais: (1º bimestre)
1.1. Revisão de matemática básica;
1.2. Conjunto dos números reais;
1.3. Produto cartesiano e plano cartesiano;
1.4. Problema de variação;
1.5. Declividade e equações da reta;
1.6. Aplicações.
2.
Funções e Gráficos: (1º bimestre)
2.1. Definição de funções e representações;
2.2. Função de variável discreta e o método dos mínimos quadrados;
2.3. Função polinomial do 1º e do 2º graus;
2.4. Função logarítmica e exponencial;
2.5. Aplicações das funções exponenciais e logarítmicas na modelagem de fenômenos
biológicos;
2.6. Aplicações.
3.
Limites: (1º bimestre)
3.1. Limites, limite infinito e limite no infinito;
3.2. Função racional;
3.3. Funções contínuas;
3.4. Aplicações.
4.
Derivada: (2º bimestre)
4.1. Definição; Interpretação geométrica; Reta tangente;
4.2. Regras de derivação;
4.3. Regra da cadeia;
4.4. Derivada da função exponencial e da logarítmica;
4.5. Derivada da função implícita;
4.6. Derivada de 2ª ordem;
4.7. Aplicações das derivadas: teste da derivada primeira e teste da derivada segunda;
4.8. Máximos e mínimos;
4.9. Ponto de inflexão;
4.10. Aplicações.
5.
Integral Definida e Indefinida: (2º bimestre)
5.1. Integrais indefinidas e propriedades;
5.2. Integrais definidas e o Teorema Fundamental do Cálculo;
5.3. Integração por substituição;
5.4. Integração por partes;
5.5. Aplicações;
5.6. Equações Diferenciais de 1ª ordem (uma noção);
5.7. Aplicações.
6.
Matrizes e Sistemas Lineares: (3º bimestre)
6.1. Definição, notação e tipos de matrizes;
6.2. Adição de matrizes e multiplicação por escalar;
6.3. Multiplicação de matrizes;
6.4. Matriz transposta;
6.5. Matrizes inversíveis.
7.
Determinantes: (3º bimestre)
7.1. Definição e propriedades;
7.2. Cálculo de determinantes.
8. Sistema de Equações Lineares (3º bimestre)
8.1. Definição e soluções;
8.2. Operações elementares;
8.3. Forma matricial de um sistema de equações lineares.
9.
Espaços Vetoriais: (4º bimestre)
9.1. Espaços vetoriais e exemplos;
9.2. Subespaços vetoriais;
9.3. Dependência e independência linear.
10.
Transformações lineares (4º bimestre)
10.1. Introdução;
10.2. Aplicações e funções;
10.3. Núcleo e imagem de uma transformação linear;
10.4. Operações com transformações lineares;
10.5. Autovalores e autovetores;
10.6. Diagonalização de operadores;
10.7. Aplicações.
4.
METODOLOGIA
4.1. PROCEDIMENTOS DE ENSINO
1.
2.
3.
Aulas expositivas.
Aulas práticas de resolução de exercícios.
Aulas no Laboratório de Computação.
4.2. ATIVIDADES DISCENTES
1.
2.
3.
Os alunos deverão assistir e participar das aulas teóricas e práticas;
Os alunos deverão realizar os trabalhos propostos pelo docente
Pesquisas na biblioteca, usando a bibliografia recomendada.
5.
CRITÉRIOS DE AVALIAÇÃO DA APRENDIZAGEM

A cada bimestre, será aplicada uma avaliação na forma de prova para que os alunos
tenham uma nota. A média final será obtida pela média aritmética das quatro notas. A
critério do Professor, poderá ser aplicada uma avaliação para substituir a pior nota obtida.
6.
BIBLIOGRAFIA
1.
2.
3.
4.
5.
6.
7.
SVIERCOSKI, R. F. Matemática Aplicada às Ciências Agrárias. Edita UFV
Universidade Federal de Viçosa. 1a. edição 2008.
Apostilas complementares
WHIPKEY, K.L. e WHIPKEY, M.N. Cálculo e suas Múltiplas Aplicações. Rio de
Janeiro: Campus, 1982.
AGUIAR, A. F. A. et al. Cálculo para Ciências Médicas e Biológicas. São Paulo:
Harbra, 1988.
BATSCHELET, E. Introdução à matemática para Biocientistas. São Paulo:
EDUSP-Interciência, 1978.
HOFFMANN, L. D. Cálculo: um curso moderno e suas aplicações. Rio de Janeiro:
LTC, 1984.
BOLDRINI; COSTA; FIGUEIREDO; WETZLER. Álgebra linear. 3.ed. São Paulo:
Harper & Row do Brasil, 1980.
Ulysses Sodré
Professor Responsável pelo Programa
Aprovado pelo Dep. em ___/___/___
Aprovado pelo Colegiado em ___/___/____
Assinatura do Chefe do Departamento
Assinatura do Coordenador do Colegiado