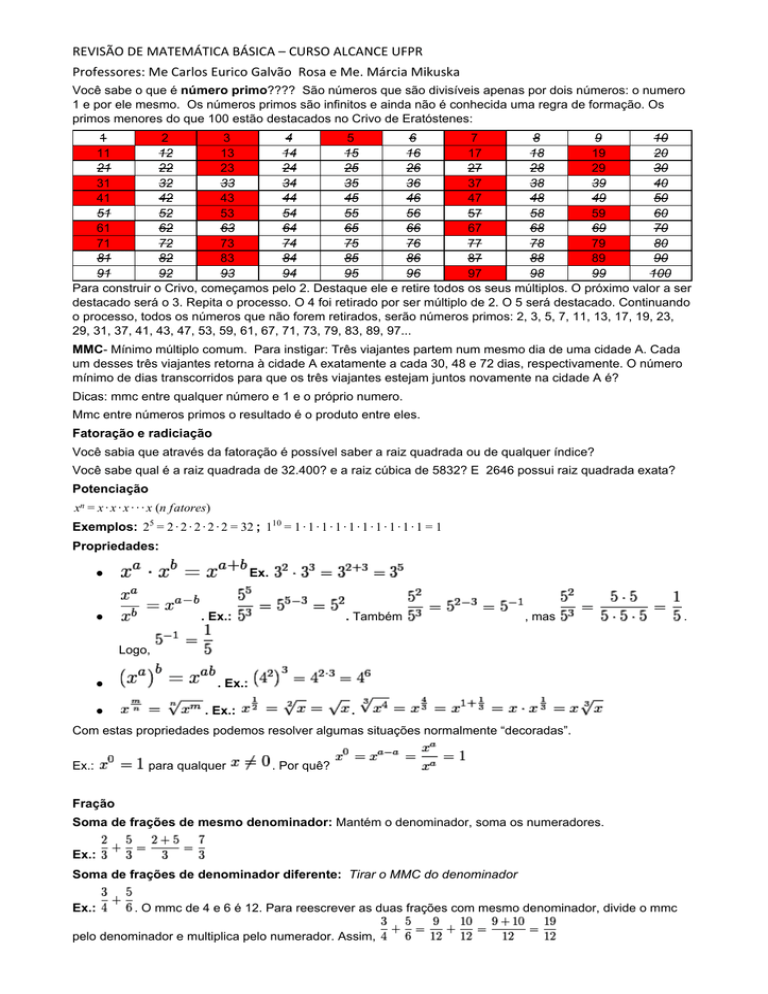
REVISÃO DE MATEMÁTICA BÁSICA – CURSO ALCANCE UFPR

 REVISÃO DE MATEMÁTICA BÁSICA – CURSO ALCANCE UFPR Professores: Me Carlos Eurico Galvão Rosa e Me. Márcia Mikuska Você sabe o que é ​número primo​???? São números que são divisíveis apenas por dois números: o numero 1 e por ele mesmo. Os números primos são infinitos e ainda não é conhecida uma regra de formação. Os primos menores do que 100 estão destacados no Crivo de Eratóstenes: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Para construir o Crivo, começamos pelo 2. Destaque ele e retire todos os seus múltiplos. O próximo valor a ser destacado será o 3. Repita o processo. O 4 foi retirado por ser múltiplo de 2. O 5 será destacado. Continuando o processo, todos os números que não forem retirados, serão números primos: ​2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97... MMC​­ Mínimo múltiplo comum. Para instigar: ​Três viajantes partem num mesmo dia de uma cidade A. Cada um desses três viajantes retorna à cidade A exatamente a cada 30, 48 e 72 dias, respectivamente. O número mínimo de dias transcorridos para que os três viajantes estejam juntos novamente na cidade A é? Dicas: mmc entre qualquer número e 1 e o próprio numero. Mmc entre números primos o resultado é o produto entre eles. Fatoração e radiciação Você sabia que através da fatoração é possível saber a raiz quadrada ou de qualquer índice? Você sabe qual é a raiz quadrada de 32.400? e a raiz cúbica de 5832? E 2646 possui raiz quadrada exata? Potenciação xn = x ∙ x ∙ x ∙ ∙ ∙ x (n fatores) Exemplos: 25 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32 ; 110 = 1 ∙ 1 ∙ 1 ∙ 1 ∙ 1 ∙ 1 ∙ 1 ∙ 1 ∙ 1 ∙ 1 = 1 Propriedades: ●
Ex. ●
​, mas ​. ●
●
​. ​Também . Ex.: Logo, . Ex.: ​. . Ex.: Com estas propriedades podemos resolver algumas situações normalmente “decoradas”. Ex.: ​ para qualquer ​. Por quê? Fração Soma de frações de mesmo denominador: ​Mantém o denominador, soma os numeradores. Ex.: Soma de frações de denominador diferente: ​Tirar o MMC do denominador Ex.: ​. O mmc de 4 e 6 é 12. Para reescrever as duas frações com mesmo denominador, divide o mmc pelo denominador e multiplica pelo numerador. Assim, Resumo Matemática Básica ­ Curso Alcance UFPR
2 “Método Borboleta” (usar com cuidado):​ O novo numerador será o produto cruzado. O novo denominador será o produto dos denominadores: ​ para chegar em Veja que desta segunda forma o resultado não sai irredutível: É preciso simplificar 1)​ ​Se ​, ​, e 2)​ ​Determine ​, então determine o valor de A. Equação do primeiro grau ​. O objetivo é encontrar o valor da incógnita “ ​”. São caracterizadas da forma: a)
b)
d)
c)
e) Polinômios A adição ou subtração algébrica de monômios é denominada polinômio, exemplo: ; . O grau de um polinômio​ reduzido, não nulo, é o grau do seu termo de maior grau. ●
●
O polinômio ​­5x​4 + 14x​5​y​2 ­ 7x​3​y​2 é do ​grau 7​, pois o seu termo de maior grau é o segundo, que é do grau ​7​. O polinômio ​4a​2​b​3​ + 5a​5​ é do ​grau 5​, pois ambos os termos do polinômio são deste grau. Redução de polinômios em termos semelhantes​: Veja abaixo alguns exemplos de redução de polinômios através da soma ou subtração de termos semelhantes: ●
●
●
Multiplicação por um monômio: Considere o exemplo: Repare que multiplicamos 7xy​ por ambos os termos do polinômio, aplicamos a propriedade distributiva da multiplicação. 2
Multiplicação de um Polinômio por um Polinômio No caso da multiplicação de polinômio por polinômio efetuamos a multiplicação de cada um dos termos do primeiro polinômio, por cada um dos termos do segundo polinômio e depois realizamos a redução do polinômio resultante. Vamos analisar a multiplicação abaixo a qual separamos em três linhas para podermos observá­la mais facilmente: Resumo Matemática Básica ­ Curso Alcance UFPR
3 Resolva com calma esses exercícios propostos: a)
h)
o)
b)
i)
p)
c)
j)
q)
k)
r)
l)
s)
d)
e)
f)
g)
m)
n)
Existe um tipo especial de multiplicação de polinômios: abordados em dois casos: Quadrado da soma: Quadrado da diferença: Quadrado da soma pela diferença: Para explicar o procedimento da ​divisão de polinômios pelo método das chaves, vamos dividir ​8a​2 ­ 2ab ­15b​2​ por ​2a ­ 3b​. A primeira coisa a verificar é se o grau do dividendo é maior ou igual ao grau do divisor. Se for menor o quociente será zero e o resto será o próprio dividendo. Repare que ambos os polinômios estão ordenados de forma decrescente em relação à incógnita ​a​: A divisão de polinômios é muito semelhante à divisão de números naturais​. Vamos começar dividindo o monômio ​8a​2​pelo monômio ​2a e colocar o quociente ​4a​ abaixo da chave: Agora vamos multiplicar por ​­4a​, o valor oposto do quociente, cada um dos monômios do divisor ​2a ­ 3b​ e colocar o resultado embaixo do dividendo: Executamos então a soma dos monômios: Continuamos a divisão baixando o terceiro monômio do dividendo: Agora dividimos ​10ab por ​2a​, que vai dar ​5b e também o colocamos abaixo da chave: Multiplicamos por ​­5b​, o valor oposto de ​5b​, cada um dos monômios do divisor ​2a ­ 3b e colocamos o resultado embaixo do primeiro resto parcial: Por fim executamos a soma que resultará em zero, indicando uma divisão exata: Equação do segundo grau: ​É definida pela forma ​. Existem alguns métodos para resolver esse tipo de equação, mas o mais comum é conhecido no Brasil pela resolução através da fórmula de Bháskara, onde temos: ​. Resumo Matemática Básica ­ Curso Alcance UFPR
4 Exemplos: a) b) Os coeficientes da equação são: a = 4, b = 8, c = 6. Substituindo esses valores na fórmula de Bhaskara, temos: Os coeficientes dessa equação são: a = 1, b = – 4, c = – 5. Agora basta aplicar esses valores na fórmula de Bhaskara: Como Δ < 0, a equação não possui raiz real. e Nesse caso, a equação tem 2 raízes reais: – 1 e 5. c) Resolva a equação incompleta do 2° grau sem utilizar a fórmula de Bhaskara: Essa é uma equação do 2° grau porque apresenta x² e é incompleta porque o coeficiente b é nulo. Para resolver essa equação sem aplicar a fórmula de Bhaskara, devemos levar o coeficiente c para o segundo membro da equação: ​. ​ são Portanto, as raízes da equação d) Outro tipo de equação incompleta, agora onde o termo c= 0; Seja a equação: Primeiramente vamos resolver a equação incompleta do 2° grau sem utilizar a fórmula de Bhaskara. Para tanto, colocaremos o x em evidência: Podemos colocar o 3 em evidência também: Como o produto entre 3x e 3x – 1 resulta em zero, devemos igualar esses dois termos a zero: Vamos agora resolver a equação através da fórmula de Bhaskara. Os coeficientes da equação são a = 9, b = – 3 e c = 0. Portanto, através de duas resoluções distintas, obtivemos que as raízes da equação e ​. ​ são Resumo Matemática Básica ­ Curso Alcance UFPR
5 R​acionalização de fração: ​Em muitos exercícios a resposta está sempre simplificada, e dessa maneira não se apresenta raízes no denominador. Então como proceder em casos onde a resposta gerou um número da forma:
​ ​,
​ ​ou
​ ​. ​E se ainda tivermos uma expressão maior no denominador? ,​ por exemplo. E ainda se a raiz não for quadrada como em
​ ​,​ o que fazer? “A matemática possui abstrações própria dos conteúdos abordados, mas com persistência e dedicação, todos podem alcançar resultados positivos”. ​ ou