Document

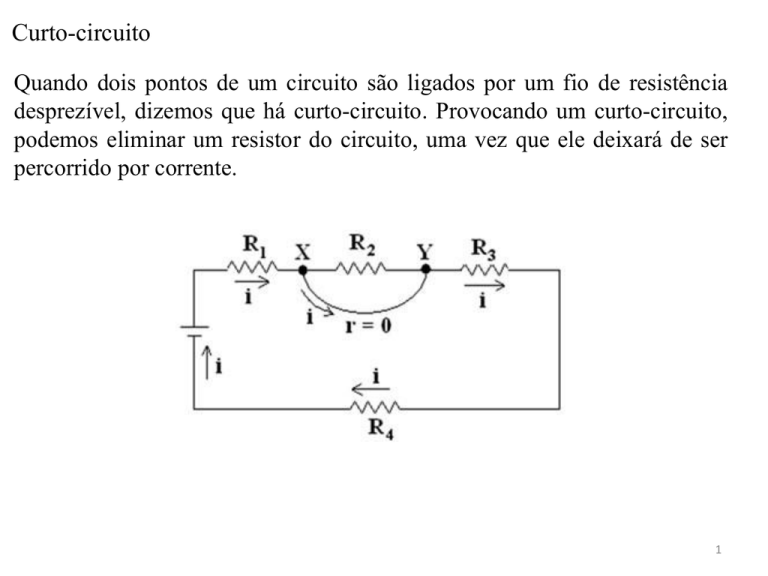
Curto-circuito
Quando dois pontos de um circuito são ligados por um fio de resistência
desprezível, dizemos que há curto-circuito. Provocando um curto-circuito,
podemos eliminar um resistor do circuito, uma vez que ele deixará de ser
percorrido por corrente.
1
2
Malha 2
Nó
Malha 1
Malha 3
3
Potência dissipada no resistor R:
Percorrendo as três malhas no sentido anti-horário:
Malha 1
Malha 2
Malha 3
4
Resistor R0 uniforme:
Portanto:
5
Portanto, do slide anterior:
6
7
8
a um potencial mais elevado
9
10
Portanto:
Do enunciado:
Mas, também podemos escrever que:
Terminal positivo
em b (Vb > Vc ).
11
Outra forma de resolver (equivalente e mais rápida)
Aplicando a lei das malhas na malha da esquerda (percorrendo a malha no sentido
anti-horário, partindo do ponto a e voltando a ele), teremos que :
Assim,
12
Item (b) Determinar a corrente através da bateria de 200,0 V
Da lei dos nós:
Mas:
Portanto:
(no sentido desenhado)
13
Item (c) Determinar a resistência R
Percorrendo a malha da direita no sentido anti-horário:
Portanto:
14
15
Item (a) Logo depois de fechar a chave S, os capacitores descarregados se
comportam como curtos-circuitos, portanto, quaisquer resistores ligados em
paralelo serão “eliminados” do circuito (não serão percorridos por corrente).
Corrente através do amperímetro
16
Item (b) Muito tempo depois de fechar a chave S, as correntes nos capacitores
tenderão a zero. Portanto, nenhuma corrente fluirá através de resistores ligados em
série com os capacitores.
17
Problema: A ponte de Wheatstone. O circuito da figura abaixo
denomina-se ponte de Wheatstone e é usado para determinar a resistência
desconhecida de um resistor R4 a partir de três resistores R1 , R2 e R3 ,
cujas resistências são conhecidas.
Como isso é feito: basta ajustar os valores das resistências R1 , R2 e R3
tal que a corrente sobre Rm seja nula.
18
Percorrendo a malha (1) no sentido horário:
Percorrendo a malha (2) no sentido horário:
Fazendo a subtração das equações:
19
Impondo a condição de que não haja corrente sobre Rm , teremos que:
Assim, da equação anterior
obtemos que:
20
Ou seja:
Mais uma vez, da condição de que não haja corrente sobre Rm :
Assim:
Observe que a relação
pode ser obtida diretamente ao percorrermos
a malha (3). Na ausência de corrente sobre Rm , partindo do ponto a e voltando a ele
teremos (no sentido horário):
Portanto:
21
Procedimento alternativo:
Da condição de que não haja corrente sobre Rm :
Ou seja:
22
Mais uma vez, da condição de que não haja corrente sobre Rm :
Portanto:
23
24
B
D
C
D
C
A
D
C
Primeira observação: as diferenças de potencial entre os pontos A e C são idênticas;
Segunda observação: as diferenças de potencial entre os pontos D e B são idênticas;
Portanto, podemos redesenhar a associação cúbica acima da seguinte maneira:
A
C
D
B
25
Portanto, teremos:
C
A
A
D
C
D
B
B
Tarefa: em vez de estarem na diagonal do cubo, refaça o problema anterior para o
caso em que os pontos A e B são os indicados na figura a seguir.
A
B
27