Exercícios Resolvidos - Teoria das Estruturas

1
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 - TEORIA DAS ESTRUTURAS I – TURMA: A - DIURNO
1º TRABALHO DE APLICAÇÃO – 1ª PARTE
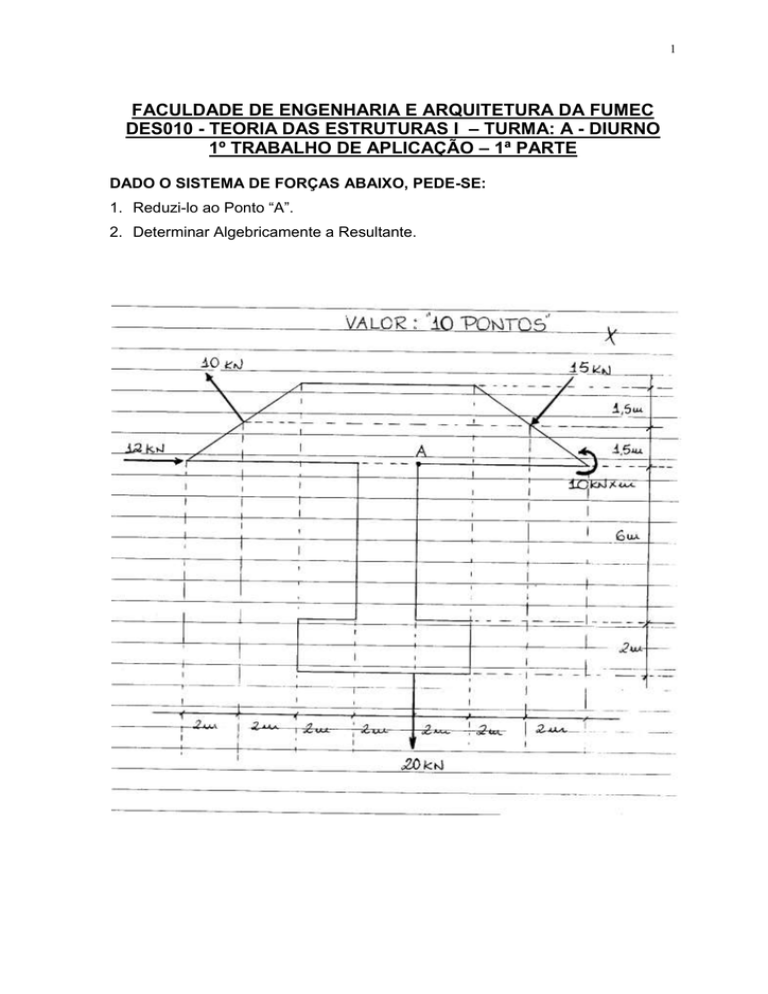
DADO O SISTEMA DE FORÇAS ABAIXO, PEDE-SE:
1. Reduzi-lo ao Ponto “A”.
2. Determinar Algebricamente a Resultante.
2
Sen  = 3/5 = 0,6
sen

= 3/5 = 0,6
Cos  = 4/5 = 0,8
cos

= 4/5
= 0,8



Rx = 12 – 10 x 0,6 – 15 x 0,6 = - 3 KN

Ry = 10 x 0,8 – 15 x 0,8 – 20 = - 24 KN
R=

(  3 ) 2  (  24 ) 2
= 24,19 KN
M A =10 x 0,8 x 6 –10 x 0,6 x 1,5 +15 x 0,8 x 4 –15 x 0,6 x1,5 –10 = 63,50 KN x m
3
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 - TEORIA DAS ESTRUTURAS I – TURMA: J
1º TRAB. DE APLICAÇÃO – 1ª PARTE – (VALOR: 10 PONTOS)
DADO A ESTRUTURA ABAIXO, PEDE-SE:
1. Reduzir o Sistema de Forças ao Ponto “A”
2. Determinar a Resultante.
4
cos  = 4/5 = 0,8
sen  = 3/5 = 0,6
cos  = 4/5 = 0,8
sen  = 3/5 = 0,6



Rx = - 4,8 – 3,6 – 10 = - 18,40 KN

R  (18,4) 2  (13,4) 2 = 22,76 KN
Ry = 15 + 4,8 – 6,4 = 13,40KN

M A = 20 + 10 x 7,5 – 4,8 x 1,5 – 6,4 x 2 – 4,8 x 4 – 3,6 x 1,5 = 50,40 KNxm
R = 22,76 KN
Ry = 13,40 KN
A
Rx = 18,40 KN
MA = 50,40 KN x m
5
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 - TEORIA DAS ESTRUTURAS I – TURMA: J - NOTURNO
1º TRAB. DE APLICAÇÃO – PARTE “B” – VALOR: 15 PONTOS
DADO O SISTEMA DE FORÇAS ABAIXO, PEDE-SE:
a - Reduzi-lo ao Ponto “A”.
b - Determinar Algebricamente a Resultante.
c - Determinar o Eixo Central.
cos  
4
 0,55
7,21
sen  
d - Determinar o Valor de cos  x.
6
 0,83
7,21
6



Rx   35,91  14   21,91 KN

Ry  48  23,79  28,84  42,95 KN
R
(21,91) 2  (42,95) 2 = 48,22 KN

M A = 35,91 x 5 + 23,79 x 8 -326 + 48 x 3 + 28,84 x 2 - 14 x 11,33 = 86,93 KN x m
C
MA
R
cos  x 

86,93
 1,80 m
48,22
 21,91
  0,45
48,22
7
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 - TEORIA DAS ESTRUTURAS I – TURMA: A - DIURNO
1º TRAB. DE APLICAÇÃO – VALOR: 25 PONTOS
DADO O SISTEMA DE FORÇAS ABAIXO, PEDE-SE:
1. Reduzi-lo ao Ponto “A”.
2. Determinar Algebricamente a sua Resultante.
3. Determinar o seu Eixo Central.
4. Calcular o cos  y .
OBS.: Utilizar para os Cálculos Duas Casas Decimais.
8



Rx  32  24  8 KN

Ry  10 17 18   9 KN

sen  = 0,8
R
cos  = 0,6
82  (9) 2 = 12,04 KN
M A   10  8,5  32  7  16  17  1,33  24  5  18  5,5   73,39 KN  m
C
MA
R
cos  y =

73,39
 6,09 m
12,04
9
  0,75
12,04
9
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 - TEORIA DAS ESTRUTURAS I – TURMA: A
1º TRABALHO DE APLICAÇÃO
DADO O SISTEMA DE FORÇAS ABAIXO, PEDE-SE:
1. Calcular Rx e Ry.
2. Determinar Algebricamente a Resultante do Sistema. Reduzir o Sistema no
Ponto “A”.
3. Calcular o cos  y.
4. Determinar o Eixo Central.
OBS.: a) Utilizar duas Casas Decimais.
b) Valor da Prova: 17 Pontos
10



Rx  20  7,1 6  21,1 KN

Ry  15  20  7,1  12,1 KN

M A  6  20  4  15  1,5  20  5,5  7,1  4,5  7,1  9,5  6  1   31 KN  m
R
( 21,1) 2  (12,1) 2  24,32 KN
C 
MA
R
cos  y 

31
 1,27 m
24,32
12,1
 0,5
24,32
11
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 – TEORIA DAS ESTRUTURAS I – TURMA: A
1º TRABALHO DE APLICAÇÃO – VALOR: 22 PONTOS
DADO O SISTEMA DE FORÇAS ABAIXO PEDE-SE:
1. Reduzi-lo ao Ponto “A”; 2. Det. Algebricamente a Resultante; 3. Det. o
Ângulo que a Resultante faz com o Eixo X; 4. Det. o Eixo Central.



Rx   30  8,04   21,96 KN
R

;
Ry   15 KN
(21,96) 2  (15) 2  26,59 KN

M A = -30 x 3 +4,02 x 3+4,02 x 6 + 4,02 x 6 – 4,02 x 7+15 x 6,67– 20 = 22,21KNxm
C
MA
R

22,21
 0,84m
26,59
3KN/m
12
RELAÇÃO DE EXERCÍCIOS SÔBRE ESFORÇOS SOLICITANTES
CALCULAR AS REAÇÕES DE APOIO E OS ESFORÇOS SOLICITANTES N,Q
e M . TRAÇAR OS DIAGRAMAS CORRESPONDENTES:



 H  0  5  H B  0  H B  5 KN
V    0  VA  VB  2  4  0  VA  VB  6 KN  VB  3,67 KN
 M B  0  VA  6  2  5  4  1  0  6 VA  14 KN  VA  2,33 KN
Seção S1 ( 0  x  1)
NS1 = - 5 KN
QS1 = VA = 2,33 KN
;
x  0  MS1  0
MS1  VAx  2,33x 
x  1  MS1  2,33 KN  m
Seção S2 ( 1  x  5)
NS2 = - 5 KN
QS2 =VA – 2 = 0,33 KN ;
 x  1  M S 2  2,33KN  m
M S 2  VA x  2 ( x  1)  2,33 x  2 ( x  1) 
 x  5  M S 2  3,67 KN  m
Seção S3 ( 0  x  1)
NS3 = - HB = - 5 KN
QS3 = - VB = - 3,67 KN
MS3 = VB x = 3,67 KN x m
13
DIAGRAMAS
14
15
VD=-29,69KN



 H  0  H A  H D  24,09 KN  H A  28,69 KN

 V  0  VA  16,97  6  24,09  VD  0  VA  VD   1,12 KN

 M A  0  16,97  3  6  8  6  6  24,09  15  24,09  9  12 H D  18VD  0
12 H D  18VD  479,25 KN

 MC ( DIR )  0   24,09  3  24,09  3  6  6H D  6 VD  0 
6H D  6VD  150,54KN (2)  12H D  12VD  301,08KN
12 H D  18VD  479,25KN
 12 H D  12VD  301,08KN
VD  29,69 KN
 6V  178,17 KN 
6HD – 6 (-29,69 KN) = 150,54  6HD = - 27,6 KN
 HD = -4,6KN
VA + VD = -1,12 KN VA = 28,57 KN
16
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 - TEORIA DAS ESTRUTURAS I – TURMA “A”
2º TRABALHO DE APLICAÇÃO
17
VA = 11,92 KN



 H  0  4  H A  H D  6,02  0  H A  H D  10,02 KN
HD = 10,02 – 10,27 HD = - 0,25KN

 V  0  VA  VD  9  9  6,02  0 VA  VD  24,02 KN
VD = 24,02 – 11,92  VD = 12,10 KN

 MD  0  HA  1 VA  12  4  1,67  9  7  9  5  6,02  1,5
-6,02 x 1,5 = 0 12 VA – HA = 132,74 KN

 M B ( ESQ)  0  3 VA  4H A  4  1,33  0 
 3VA  4H A  5,32 KN
12VA  H A  132,74 KN  (4)
 48VA  4H A  530,96 KN
3VA  4H A  5,32 KN
 45VA  536,28 KN  VA  11,92KN
CÁLCULO DE HA :
3 x 11,92 – 4 HA = - 5,32KN  - 4 HA = - 41,08 KN  HA = 10,27 KN
18
1ª QUESTÃO:


 H  0  H A  6  0  H A  6 KN
 V   0  VA  6  8  0  VA  14 KN

 M A  0  M A  6  (4  1)  8 ( 2  7)  6 1,5  0
 M A  30  72  9 M A  111 KN  m
19
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 – TEORIA DAS ESTRUTURAS I – TURMA J
2º TRABALHO DE APLICAÇÃO
DADA A ESTRUTURA ABAIXO, PEDE-SE CALCULAR AS REAÇÕES DE
APOIO.
OBS.: UTILIZAR DUAS CASAS DECIMAIS.
20
4 KN/m
VA = - 14,79 KN



 H  0  H A  H E  12  0  H A  H E  12 KN H A  0,75 KN

 V  0  VA  VE  9  6  3  28,84  0 VA  VE  46,84 KN
VA  32,05  46,84KN VA  14,79 KN

 M A  0  12  2  9  1,5  6  6  3  7  8  6  28,84  13  15VE  2H E  0 
15VE  2H E  455,22 KN

 MD( DIR)  0  6  28,84  2  6 HE  4VE  0 

4VE  6H E  51,68KN
15VE  2H E  455,22KN  (3) 
4VE  6 H E  51,68 KN
 45VE  6 H E  1365,66 KN
 41VE  1313,98 KN
VE  32,05 KN
CÁLCULO DE HE :
4 x 32,05 + 6 HE = 51,68 KN  6 HE = - 76,52 KN  HE = - 12,75KN
21
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 – TEORIA DAS ESTRUTURAS I
TURMA: J – EXAME ESPECIAL
1ª QUESTÃO: VALOR: 22 PONTOS
DADA A ESTRUTURA ABAIXO, PEDE-SE CALCULAR:
a - Reações de Apoio.
b - Os Esforços Solicitantes N, Q e M.
c - Traçar os Diagramas Correspondentes.
cos  = 0,8
sen  = 0,6
OBS.: “UTILIZAR DUAS CASAS DECIMAIS”.

 M A  0  M A  36  3  20  2  0  M A  148 KN  m
22
SEÇÃO S1 ( 0  y  6 )
NS1 = - VA = - 20 KN
S1
 y  0  S1  36 KN
= - HA + 6y  -36 + 6 y 
 y  6  S1  0
MS1 = - MA – 6 y x y / 2 + HAy  - 148 – 3y2 + 36y
y  0  M  148 KN  m
S1


2
- 148 – 3y + 36y y  3  MS1  67 KN  m
y  6  M   40 KN x m
S1

( MÁX )

SEÇÃO S2 ( 0  Z  5 )
NS2 = - 4 sen  z = - 2,4z
 S2 =
 4 cos    3, 2 KN

 3,2 z
z  0  N S1  0
z  5  N S1  12 KN
 z  0 S 2  0

 z  5 S 2  16 KN
z  0  M S2  0

MS2 = - 3,2 z x z/2  1,6z z  2,5  M S2  10 KN  m
z  5  M   40 KN  m
S2

2
23
FACULDADE DE ENGENHARIA E ARQUITETURA DA FUMEC
DES010 – TEORIA DAS ESTRUTURAS I - TURMA: A
EXAME ESPECIAL
1ª QUESTÃO: VALOR: 22 PONTOS
DADA A ESTRUTURA ABAIXO, PEDE-SE:
01 – Calcular as Reações de Apoio;
02 – Calcular os Esforços N , Q e M;
03 – Traçar os Diagramas Correspondentes.
24
2 KN/m
2
6
2x
 p 
 0,33x
p
x
6


 H  0  H A  H B  8 KN  H A  1,25 KN

 V  0  VA  VB  12 KN  VA  10 KN

 M A  0  4H B  9VB  6  5  8  2  6  1,5  0 
 9VB  4HB  55 KN  9  2  4HB  55 KN  HB  9,25 KN
M

D ( DIR )
 0  6  2  6VB  0  VB  2 KN
SEÇÃO S1 ( 0  x  6 )
NS1 = - HB = - 9,25 KN
p
0,33 x 2
 2 
2
2
0,17 x 2  2  0  x  2
 3,43
0,17
S1   VB 
 x  0  S1  2 KN

 x  3,43  S1  0
 x  6    3,94 KN
S1

25
x
x
p
3
MS1 = VB x  0,33 x  2 x  0,06 x 
x
2

x

 0  MS1  0
 2  MS1  3,52 KN  m
 3,43  MS1  4,44 KN x m
( MÁX )
 6  MS1  0
SEÇÃO S2 ( 0  z  2,5)
NS2 = - VA sen  + HA cos  = - 8,75 KN
S2 = VA cos  + HA sem  = 5 KN
 z  0  M S2  0
MS2 = (VA cos  + HA sen ) z = 5 z 
 z  2,5  M S2  12,50 KN  m
SEÇÃO S3 ( 2,5  z  5 )
NS3 = NS2 = - 8,75 KN
S3
= VA cos  + HA sen  - 10 = - 5 KN
 z  2,5  MS3  12,5 KN  m
MS3 = 5z - 10 ( z – 2,5) 
 z  5  MS2  0
26