Acionamento de motores CC

METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
ELETRÔNICA DE POTÊNCIA I
CONTROLE DE MALHA FECHADA PARA MOTORES CC
Parte 2 – Modelagem do Conversor e Sincronização para Disparo
Para qualquer sistema operando em malha fechada é fundamental conhecer o
modelo de cada bloco do sistema de modo a facilitar tomadas de decisão
consistentes e efetivas sobre o sistema real. No caso do motor CC de campo
independente a modelagem do motor já foi elaborada, a próxima etapa é a
modelagem do conversor CA-CC, ou seja do retificador controlado.
Vamos admitir que o conversor esteja atuando sobre uma carga muito indutiva,
ou que haja um indutor de filtragem de corrente no circuito de armadura do
motor e o conversor pode ser monofásico ou trifásico usando um esquema de
disparo pelo coseno ou por rampa, sendo que o primeiro fornece uma relação
linear entre a tensão de controle Ec(s) e a tensão controlada na armadura Ea(s) e
o segundo apresenta uma condição não linear, mas que localmente pode ser
tratada como linear. Se desprezarmos o pequeno retardo associado ao
conversor teremos, considerando a carga muito indutiva com continuidade de
corrente, onde valem as expresões:
Conversor pleno monofásico:
Conversor pleno trifásico:
onde Vs é a tensão eficaz de fase e α o ângulo de disparo dos tiristores.
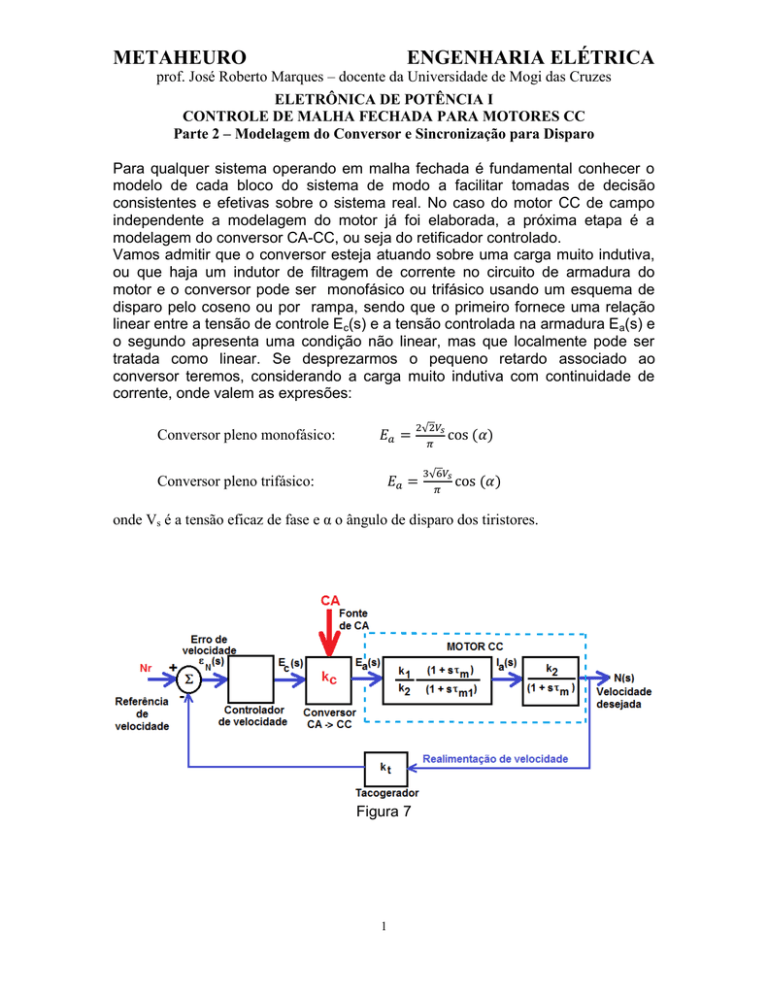
Figura 7
1
METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
Se um tacogerador for conectado ao eixo do motor, um sinal de velocidade pode
ser realimentado e o erro N ( s) , pode ser utilizado para controlar a tensão de
armadura através da tensão de controle EC. Este esquema é mostrado na figura
7.
A modelagem do conversor monofásico utilizando o método do coseno
No acionamento pelo coseno geramos uma tensão de controle correspondente
ao coseno da onda senoidal de alimentação do conversor e utilizamos esse sinal
cosenoidal para comparar com uma tensão de controle que pode ser gerada
localmente via potenciometro ou por uma malha de controle. O esquema dos
sinais é mostrado na figura 8.
Figura 8
O esquema para a geração dos sinais mostrados na figura 8 é mostrado na
figura 9.
2
METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
Figura 9 Acionamento pelo coseno (monofásico)
Admitindo que a tensão no secundário do transformador TR1 é dada pela
expressão (15), a tensão na saída mesmo é dada pela expressão (16).
(15)
(16)
Quando aplicada nas entradas dos comparadores LM311 e esse sinal se iguala
a tensão de controle EC, temos a expressão (17).
(17)
Substituindo a expressão (17) na equação do conversor monofásico, obtemos a
expressão (18).
E portanto:
(18)
A modelagem do conversor monofásico utilizando o método da rampa
No acionamento pela rampa utilizamos um amplificador operacional para
detectar os semiciclos da onda senoidal e sincronizar o gerador de rampa que é
basicamente um integrador com circuito de reset.
As formas de onda mostradas na figura 10 correspondem a (A) tensão na saída
do transformador TR1, cuja finalidade é sincronizar o sistema de gatilhamento
dos SCRs e gera a rampa que detecta o ângulo de controle desejado.
3
METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
A forma de onda (B) verde indica tensão na saída do amplificador operacional
que detecta a fase da tensão de amostra da rede e sincroniza o gerador de
rampa (C).
A rampa gerada é comparada com a tensão de controle Ec e gera os pulsos de
duração do sistema de acionamento dos gatilhos (D).
Note que nesse ponto ainda não definimos qual será o pulso de gatilhamento
dos SCR de T1 e T3 (admitidos aqui acionarem o semiciclo da rede) e T2 e T4
que acionam o outro semiciclo, isso deve ser feito em uma operação lógica AND
entre os sinais de sicronismo da rede (B) e o sinal de gatilhamento (D).
Figura 10
A modelagem matemática do sistema de geração do sinal de gatilhamento inicia
com a equação de saída do gerador de rampa dada por (20).
(20)
Om sinal de controle é gerado quando a função rampa fica menor que a tensão
de controle Ec, no ponto onde ambas igualam podemos escrever a expressão
(210.
4
METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
(21)
Que define o ângulo α de acordo com a expressão dada por (22).
(22)
Substituindo na expressão do conversor monofásico, já discutida temos a
expressão (23).
(23)
A expressão (23) mostra que a tensão de armadura da máquina varia com o
coseno quando utilizamos a disparo baseado na rampa e portanto, é não-linear.
A figura 11 mostra um circuito que implementa as formas de onda da figura 10 a
partir de uma amostra da tensão da rede com a finalidade de sincronizar o
gerador de rampa resetável. A maior parte dos amplificadores operacionais é
utilizada para conformar a rampa no modo desejado.
Figura 11
Aplicando o processo de linearização na expressão que relaciona a tensão de
saída do conversor com a tensão de controle, obtemos a expressão (24).
Admitindo que o conversor esteja operando em um determinado ponto de
operação
a partir de uma tensão de controle
então para pequenas
variações em torno desse pondo de operação a variação da tensão de armadura
do conversor
em relação a variações na tensão de controle
é dada pela
expressão:
5
METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
Que corresponde ao valor de kC desejado para pequenos sinais.
Exercícios:
1) Projetar um controlador de ângulo de fase de um retificador monofásico
em ponte com carga muito indutiva utilizando o método do coseno. O
transformador de entrada é de 220/9V (ef) e a tensão de controle E C
máxima é de 10V e -10V. Utilize um capacitor de 100nF no integrador.
Discutir o efeito da variação da rede elétrica em cerca de ± 20% sobre o
valor de pico do coseno gerado e côo isso afeta o ângulo de controle.
Solução:
Como a tensão de controle é de 10V, então a tensão de pico do gerador
de coseno também deve ser de 10, assim:
Para uma variação de ±20% na tensão da rede elétrica, qual será a
variação na tensão de pico da onda cosenoidal?
6
METAHEURO
ENGENHARIA ELÉTRICA
prof. José Roberto Marques – docente da Universidade de Mogi das Cruzes
Assim a ocorrência do erro é de ±2,2% sendo que o aumento da tensão de fase
diminui a tensão da carga em 2,2% o que indica que o ângulo de controle
aumenta o valor de α, o que diminui a tensão média na carga e o inverso ocorre
quando a tensão de fase diminui.
Essas variações sugerem que utilizemos um gerador de onda cosenoidal
independente da tensão da rede, algo do tipo PLL (Phase Locked Loop), ou um
sistema de comparação baseado em sistemas digitais com um tabela de
cosenos armazenada na memória de um microcontrolador, a consulta a tabela
deve ser sincronizada com a rede elétrica para garantir a fase correta do gerador
de coseno.
2) Projetar um controlador baseado no gerador de rampa para a situação em
que ECmax=10.
Embora o controlador baseado na rampa tenha a desvantagem de operar
de forma não linear, ele é independente das variação da tensão da rede,
ou seja o ângulo de disparo muda é invariável uma vez que a rampa não
é alterada pelas variações da tensão da rede, mas obviamente ocorre
variação na tensão média aplicada ao motor em função da variação de
Vs.Admita que a tensão do alimentador da rampa esta relacionada com o
divisor de tensão dado na figura abaixo. Utilize um capacitor de 10nF na
rede de 60Hz.
7