Circuitos em Série Um circuito consiste em um número qualquer de

Circuitos em Série
Um circuito consiste em um número qualquer de elementos unidos por seus terminais, com pelo
menos um caminho fechado através do qual a carga possa fluir.
Dois elementos de circuitos estão em série se possuem somente um terminal em comum, terminal
este que não está conectado a outro elemento percorrido por corrente.
Na figura acima, os resistores R 1 e R2 estão em série porque possuem somente um ponto em
comum, o ponto b. As outras extremidades dos resistores estão ligadas a outros pontos do circuito.
Pela mesma razão, a bateria E está em série com o resistor R 1, tendo o terminal a em comum, e em
série com R2, tendo o terminal c em comum.
Se no terminal b do circuito for conectado um terceiro componente, como na figura abaixo, os
resistores R1 e R2 não estarão mais em série.
Como consequência direta dessa definição, pode-se dizer que quando dois ou mais elementos de um
circuito estão conectados em série, a corrente é a mesma para todos eles.
Considerando o circuito resistivo mostrado na primeira figura, a bateria E fornece uma tensão, e
como consequência uma corrente flui pelo circuito. Pela Lei de Ohm, haverá uma resistência
elétrica que relaciona essas duas grandezas, a resistência. Como estão sendo consideradas a tensão
total fornecida pela bateria e a corrente total que flui pelo circuito, essa resistência será a
equivalência de todas as resistências do circuito. Para circuitos em série, a resistência equivalente de
duas ou mais resistências será a soma delas.
Uma vez conhecida a resistência equivalente, o circuito pode ser redesenhado. Para o circuito da
primeira figura, as duas resistências R1 e R2 podem ser substituídas pela resistência equivalente.
Conhecendo os valores de tensão e corrente para cada elemento do circuito, é possível calcular a
potência fornecida ou consumida por cada um.
A potência total fornecida a um circuito resistivo é igual à potência total dissipada por cada um dos
elementos resistivos. Em outras palavras, seja P1 a potência dissipada pelo resistor R1, um circuito
com n resistores terá a potência dissipada:
Pdissipada = P1 + P2 + … + Pn
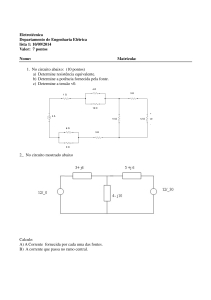
Exemplo: para o circuito da figura abaixo:
a) Encontre a resistência equivalente.
b) Calcule a corrente fornecida pela fonte.
c) determine as tensões V1, V2 e V3.
d) Calcule a potência dissipada em R1, R2 e R3.
e) Determine a potência fornecida pela fonte e compare com o resultado anterior.
Duas ou mais fontes de tensão também podem ser ligadas em série, para aumentar ou diminuir a
tensão total fornecida ao circuito. A tensão resultante é determinada somando-se as tensões das
fontes, levando-se em consideração o sentido da tensão (do menor para o maior potencial).
Exemplo: a tensão total da associação de baterias abaixo é:
Etotal = E1 + E2 + E3 = 10 + 6 + 2 = 18 V
Exemplo: a tensão total da associação de baterias abaixo, considerando o sentido positivo para a
direita:
Etotal = E1 - E2 - E3 = 4 - 9 - 3 = -8 V
O que resulta em uma tensão de 8 V para a esquerda.
Lei de Kirchhoff das Tensões
A Lei de Kirchhoff das Tensões (LKT) afirma que a soma algébrica das variações de potencial em
uma malha fechada é nula, onde uma malha fechada é qualquer caminho contínuo que deixa um
ponto em um sentido e retorna ao mesmo ponto vindo do sentido oposto, sem deixar o circuito.
Para podermos aplicar a LKT, a soma das tensões precisa ser feita percorrendo a malha em um
sentido. Um sinal positivo indica um aumento de potencial (do menor para o maior), e um sinal
negativo, uma queda (do maior para o menor).
Na figura acima, iniciando pelo ponto a, no sentido horário, encontramos primeiro uma queda de
potencial V1, de a para b, e depois V2, de b para c/d. Entre os pontos d e a, encerrando a malha
fechada, há um aumento de potencial E. Assim, segundo a LKT:
- V1 – V2 + E = 0
E = V1 + V2
A equação acima mostra outra consequência direta da associação de elementos em série (no caso
acima, os dois resistores): a tensão total da associação é a soma das tensões de cada elemento.
Observe que se o sentido de análise dos circuitos for invertido, considerando o sentido anti-horário,
a LKT se mantém válida.
A aplicação da LKT não precisa seguir necessariamente um caminho percorrido por corrente. Por
exemplo, considerando o circuito da figura abaixo, é possível determinar a tensão Vab:
Vab – 8 + 12 = 0
Vab = -4 V
Considerando o sentido analisado (horário), a tensão V ab é negativa, o que significa que de a para b
há uma queda de potencial, portanto a tensão está orientada para a esquerda.
Exemplo: Determine a tensão Vx no circuito abaixo.
Os elementos de circuitos em série podem ser intercambiados sem que a resistência equivalente, a
potência fornecida e consumida e corrente que os atravessa sejam alterados.
Exemplo: Determine a corrente total no circuito abaixo.
Considerando a Lei de Ohm e as características da conexão em série, é possível perceber que a
tensão entre os terminais dos elementos resistivos se divide na mesma proporção que os valores de
resistência. Essa propriedade é chamada de divisor de tensão.
Exemplo: Considerando o circuito da figura abaixo, calcule as tensões em cada resistência.
Repare que o valor das tensões em cada resistor é numericamente o dobro do valor das resistências,
pois a corrente em todos eles é 2 A.
Em sistemas eletrônicos, os circuitos podem ser aterrados por questão de segurança. Entretanto, é
comum representar o ponto de terra em circuitos, ilustrando uma mera referência de tensão, pois o
ponto de terra é considerado sempre um potencial elétrico nulo.
Circuitos em Paralelo
Dois elementos, ramos ou circuitos estão ligados em paralelo quando possuem dois pontos em
comum.
No caso de associação em paralelo de resistências, também é possível determinar a resistência
equivalente da associação. Esse valor equivalente, no entanto, é diferente da associação em série.
Para associações em paralelo, a condutância total é a soma das condutâncias, onde condutância é
definida como o inverso da resistência (G = 1/R).
Para o circuito da figura acima, a condutância total G T é dada pela soma de G1 a GN. Substituindo os
valores de condutância por resistência, temos:
1
1 1
1
= + +⋯+
RT R1 R2
RN
Exemplo: Para o circuito da figura abaixo, (a) calcule a resistência equivalente, (b) determine a
corrente total fornecida pela fonte, (c) Calcule as correntes em R1 e R2, (d) calcule a potência
consumida por cada resistência e (e) a potência fornecida pela fonte.
Lei de Kirchhoff das Correntes
A Lei de Kirchhoff das Corrente (LKC) afirma que a soma algébrica das correntes que entram e
saem de uma região, sistema ou nó, é igual a zero. Essa lei é utilizada mais frequentemente no caso
de junção (ou nó), onde se encontram dois ou mais caminhos para a corrente.
Exemplo: Encontre o valor das correntes I3, I4, I6 e I7.
Se os elementos em paralelo tiverem resistências diferentes, o elemento de menor resistência será
percorrido pela maior fração de corrente. A razão entre os valores das correntes nos dois ramos será
inversamente proporcional à razão entre as resistências. Essa propriedade é chamada divisor de
corrente.
Exemplo: Na associação em paralelo abaixo, sabendo a corrente em um resistor, é possível
determinar a corrente nos resistores restantes através de proporção.
Duas ou mais fontes de tensão também podem ser conectadas em paralelo, para aumentar a corrente
fornecida, prolongando a vida útil de uma bateria. Se duas baterias de valores diferentes forem
ligadas em paralelo, acabarão ambas descarregadas ou seriamente danificadas, pois a tendência da
bateria de tensão mais elevada é cair rapidamente até igualar-se à da fonte de tensão mais baixa.
Pela LKC, a corrente total fornecida por uma associação em paralelo de baterias, será a soma das
correntes de cada uma.
Circuito aberto e curto-circuito
Um circuito, ou malha, é considerada aberta quando não há um caminho para passagem de corrente
elétrica. Nesses casos, a corrente nessa parte do circuito é nula. A tensão, no entanto (como foi visto
anteriormente) não precisa de um caminho fechado para existir, somente os valores de potencial
elétrico em dois pontos.
Exemplo: Determine a tensão Vab.
Podemos resumir então que, em nas porções onde tem-se um circuito aberto, a corrente é igual a
zero, mas a tensão pode ter um valor finito.
Um curto-circuito, por outro lado, acontece quando conectamos os dois terminais de um sistema
com um elemento de resistência muito baixa, ou nula. Ao fazermos essa conexão, a diferença de
potencial entre os terminais conectados também é zero, pois V = Ri = (0) i = 0.
Matematicamente, a corrente em um curto-circuito é infinita, dada pela Lei de Ohm. A corrente do
curto-circuito, no entanto, dependerá do sistema que está ligado ao curto.
Exemplo: Calcule a corrente I no circuito abaixo.
Circuitos em série e paralelo
Os diversos elementos que compõem um circuito elétrico, geralmente são conectados em arranjos
em série e paralelo. Para solucionar problemas dessa natureza, pode-se utilizar quaisquer
metodologia, tais como cálculo de resistência equivalente, Lei de Ohm ou as Leis de Kirchhoff.
Com a prática, a escolha do método se torna intuitiva.
Por exemplo, circuitos onde as resistências são conectadas em cascata, calcular a resistência
equivalente e aplicar a Lei de Ohm é, geralmente, mais prático. Em circuitos com mais de uma
fonte de tensão, a aplicação das Leis de Kirchhoff costuma ser mais eficiente.
Exemplo: Calcule as correntes e tensões indicadas.
Exemplo: Determine as tensões V1 e V2 e a corrente I.
Quando um potenciômetro é ligado ao circuito, a tensão envolvendo o terminal intermediário
depende da razão entre os valores de resistência envolvendo os 3 terminais (divisor de tensão).
Quando esse potenciômetro é conectado a uma carga, a tensão de saída passa a depender também da
resistência da carga.
No caso acima, a tensão passa a ser
V C=
R'VC
R ' +R2
onde R' = R1 || RC. Se for desejável o controle da tensão de saída a partir do potenciômetro, é
aconselhável que RC >> RT.
Exemplo: No circuito da figura abaixo, determine a tensão de saída do potenciômetro linear de 1
MΩ, considerando que o terminal de saída (intermediário) está no ponto médio do potenciômetro e
não há carga conectado a ele. Repita os cálculos considerando uma carga de 100 Ω conectada ao
potenciômetro.