V - Rede La Salle

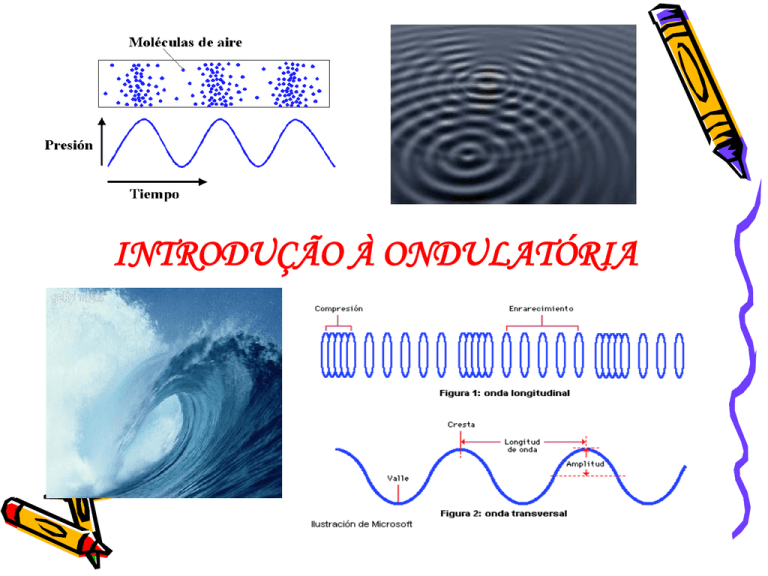
INTRODUÇÃO À ONDULATÓRIA
Considerações Iniciais
Considerações Iniciais: O que é ONDA ???
Perturbação produzida:
PULSO
O PULSO se movimenta a partir da
região onde foi gerado: ONDA
A onda se movimenta transferindo energia
através da vibração que é produzida pelo pulso.
ONDA transfere ENERGIA através do meio,
SEM TRANSPORTAR MATÉRIA !!!
Para realizar as manobras, o surfista
precisa remar para entrar na onda e
após...se movimentar constantemente...
Classificação das Ondas: Quanto a Natureza
MECÂNICAS: Precisam do meio material para se propagar.
Ex:
Ondas no mar
Ondas na superfície
de um lago
Ondas em molas
Ondas em cordas
Ondas sonoras
ELETROMAGNÉTICAS: Não precisam do meio material
para se propagar.
Ex:
Raios X
Ondas de Rádio
Ondas de Luz
Raio Laser
Classificação das Ondas:
UNIDIMENSIONAIS:
Quanto a
Propagação
BIDIMENSIONAIS:
Apenas 1 direção de
propagação.
2 direções de
propagação.
Ex: Ondas em cordas
Ex: Ondas em lagos
Direção
de
TRIDIMENSIONAIS:
3 direções de
propagação.
Ex: Ondas Sonoras
Classificação das Ondas:
Quanto a
Vibração
Direção
de
TRANSVERSAIS:
LONGITUDINAIS:
Propagação perpendicular à
vibração
Vibração e propagação na
mesma direção.
Ex: Ondas em Cordas
Ex: Ondas em Molas
e o Som
ONDAS PERIÓDICAS:
λ comprimento de onda
crista
crista
A
A
vale
vale
λ comprimento de onda
Grandezas fundamentais das ondas:
Frequência: número de ondas por tempo
Acinhó: f = nº de ondas/tempo
No SI, dada em hertz (Hz)
Porém, usualmente, pode ser dada em rpm!
Neste caso:
rpm/60 = Hz
Período: tempo de duração de uma onda completa
No SI, dado em segundo (s)
A relação entre frequência e período é:
f = 1/T
Equação Fundamental da Ondulátória:
Sendo constante a
velocidade de propagação
de uma onda, temos:
x=v.t
Acinhó: =v.T
=v.1/f
Ou, ainda:
V=λ.f
V: velocidade de propagação da onda
λ: comprimento da onda
f: frequência das oscilações
A velocidade de propagação da onda
só depende do meio de
propagação.!!!!
Velocidade da Onda numa Corda:
A velocidade de propagação de uma onda numa corda obedece a
equação de TAYLOR
V 
T

T: força tensora na corda
μ: densidade linear da corda
massa (kg)

comprimento (m)
Exercícios de Sala:
1) Uma corda de comprimento 3 metros e massa 60 gramas é mantida
tensa sob a ação de uma força de intensidade 800 N. Determine a
velocidade de propagação de um pulso nessa corda.
m

L
0,06 kg

3m
  0,02 kg / m
V 
V
T

800
0,02
V  200 m / s
2) Uma corda de massa 240 gramas e de comprimento 1,2 metros vibra com
frequência de 150 Hz, conforme indica a figura:
0,4
0,4
0,4
a) Qual a velocidade de propagação da
onda na corda ?
  0,8 m
v  f
v  0,8  150
v  120 m / s
b) Qual a intensidade da força tensora na corda ?
m

L

0,24
1,2
  0,2 kg / m
V 
120 
T

T
0,2
T  2880 N
Reflexão de Pulsos em uma Corda:
EXTREMO FIXO
INVERTE FASE
EXTREMO LIVRE
NÃO INVERTE FASE
Refração de Pulsos em uma Corda:
1) Da Corda GROSSA para a Corda FINA:
vA
μ MAIOR
V 
μ MENOR
T

f NÃO MUDA
vB
V AUMENTA
μ DIMINUI
Observe que aqui ocorre uma
REFRAÇÃO e também uma
REFLEXÃO SEM INVERTER
a fase.
λ AUMENTA
VB > VA
λB > λA
Refração de Pulsos em uma Corda:
1) Da Corda FINA para a Corda GROSSA:
V 
vA

f NÃO MUDA
μ MENOR
μ MAIOR
“CORDA LEVE”
“CORDA PESADA”
vB
T
V DIMINUI
μ AUMENTA
λ DIMINUI
VB < VA
Observe que aqui ocorre
REFRAÇÃO e também
REFLEXÃO COM
INVERSÃO de fase.
λB < λA
Exercícios de Sala:
3) Uma onda periódica propaga-se em uma corda A, com velocidade 40 cm/s e
comprimento de onda 5 cm. Ao passar para uma corda B, sua velocidade passa a
ser 30 cm/s. Determine:
a) O comprimento de onda no meio B;
VA = λA . fA
b) A freqüência da onda.
40 = 5 . fA
40 cm/s
fA = 8 Hz
VB = λB . fB
30 cm/s
30 = λB . 8
λB = 3,75 cm
INTERFERÊNCIA:
A1
A2
A1
A2
A1
A2
A1
A2
CONSTRUTIVA:
DESTRUTIVA:
Amplitude Resultante
Amplitude Resultante
A = A1 + A2
A = A 1 - A2
ONDAS ESTACIONÁRIAS:
Encontro de duas ondas,
uma incidente e outra
refletida, de mesma f, A e
λ que se propagam em
sentidos opostos
VENTRE
NÓ
λ/2
λ
Exercícios de Sala:
4) Uma onda estacionária de freqüência 8 Hz se estabelece numa linha fixada
entre dois pontos distantes 60 cm. Incluindo os extremos, contam-se 7 nodos.
Calcule a velocidade da onda progressiva que deu origem à onda estacionária.
60 cm
λ = 20 cm
V=λ.f
V = 20 . 8
V = 160 cm/s
Exercícios de Sala:
07) A figura abaixo é a representação gráfica, num dado instante,
de duas ondas A e B que se propagam com a mesma velocidade ao
longo de duas cordas. A frequência da onda A é 10 Hz. Julgue as
afirmativas como verdadeiras ou falsas.
λA
AA
01) O comprimento da onda A é maior que o da onda B.
λA
λB
λA > λB
02) A velocidade de propagação das ondas é de 0,50 m/s.
VA = λA . fA
VA = 0,05 . 10
VA = VB = 0,5 m/s
04) É possível variar a amplitude da onda A sem que se altere sua freqüência.
Isso é perfeitamente possível, pois AMPLITUDE e FREQUÊNCIA,
NÃO SE RELACIONAM...!!!!
08) As ondas representadas são do tipo longitudinal.
Afirmação falsa, pois a
figura nos mostra ondas
transversais..!!!
16) A amplitude da onda A é de 5,0 cm.
Ligue-se !!!
A amplitude vale
2 cm.
32) O período da onda B é maior que 0,10 s.
fA = 10 Hz
TA = 0,1 s
Se λB < λA , então fB > fA
Assim: TB < TA
Cháuziimmm!!!