Simulado para a Escola Naval

Simulado Folião de Elite
Simulado
Escola Naval 2017
Física
01. Em um local onde g  10m / s2 , um objeto é lançado verticalmente para cima, a partir do solo terrestre. O
efeito do ar é desprezível.
O objeto atinge 20% de sua altura máxima com uma velocidade de módulo igual a 40 m/s. A altura máxima
atingida pelo objeto vale:
a) 200 m
b) 150 m
c) 100 m
d) 75 m
e) 80 m
02. Um automóvel parte do repouso em uma via plana, onde desenvolve movimento retilíneo uniformemente
variado. Ao se deslocar 4,0 m a partir do ponto de repouso, ele passa por uma placa sinalizadora de trânsito e,
4,0 s depois, passa por outra placa sinalizadora 12 m adiante. Qual a aceleração desenvolvida pelo
automóvel?
a) 0,50 m s2 .
b) 1,0 m s2 .
c) 1,5 m s2 .
d) 2,0 m s2 .
e) 3,0 m s2 .
03. Uma partícula com carga q e massa M move-se ao longo de uma reta com velocidade v constante em
uma região onde estão presentes um campo elétrico de 1,0  106 mV / m e um campo de indução magnética de
0,10 T. Sabe-se que ambos os campos e a direção de movimento da partícula são perpendiculares entre si.
Determine a velocidade da partícula.
a) 1,0  103 m / s
b) 1,0  107 m / s
c) 1,0  104 m / s
d) 1,0  107 m / s
e) 1,0  103 m / s
TEXTO PARA A PRÓXIMA QUESTÃO:
Considere os dados abaixo para resolver a(s) questão(ões), quando for necessário.
Constantes físicas
Aceleração da gravidade próximo à superfície da Terra: g  10m s2
Aceleração da gravidade próximo à superfície da Lua: g  1,6m s2
Densidade da água: ρ  1,0 g cm3
Velocidade da luz no vácuo: c  3,0  108m s
Constante da lei de Coulomb: k0  9,0  109 N  m2 C2
04. Duas cargas elétricas fixas estão separadas por uma distância d conforme mostra o esquema seguinte.
1
Simulado Folião de Elite
Os pontos sobre o eixo x, onde o campo elétrico é nulo, estão localizados em
a) x  (2  2)  d e x  (2  2)  d.
b) x  (2  2)  d e x  (2  2)  d.
c) x  (2  2)  d e x  (2  2)  d.
d) x  (2  2)  d.
e) x  (2  2)  d.
05. Uma barra de coeficiente de dilatação α  5π  104 C1, comprimento 2,0 m e temperatura inicial de 25 C
está presa a uma parede por meio de um suporte de fixação S. A outra extremidade da barra B está
posicionada no topo de um disco de raio R  30 cm. Quando aumentamos lentamente a temperatura da barra
até um valor final T, verificamos que o disco sofre um deslocamento angular Δθ  30 no processo. Observe a
figura a seguir:
Supondo que o disco rola sem deslizar e desprezando os efeitos da temperatura sobre o suporte S e também
sobre o disco, calcule o valor de T.
a) 50 C
b) 75 C
c) 125 C
d) 300 C
e) 325 C
2
Simulado Folião de Elite
06.
Um espelho plano gira na velocidade angular constante ω em torno de um ponto fixo P, enquanto um objeto
se move na velocidade v , de módulo constante, por uma trajetória não retilínea. Em um determinado instante,
a uma distância d do ponto P, o objeto pode tomar um movimento em qualquer direção e sentido, conforme a
figura acima, sempre mantendo constante a velocidade escalar v . A máxima e a mínima velocidades escalares
da imagem do objeto gerada pelo espelho são, respectivamente
a) ωd  v e ωd  v
b) ωd  v e
c)
 ωd2  v2
 ωd2  v2 e
ωd  v
d) 2ωd  v e 2ωd  v
e) 2ωd  v e
 2ωd2  v 2
07. Ao passar pelo ponto O, um helicóptero segue na direção norte com velocidade v constante. Nesse
momento, um avião passa pelo ponto P, a uma distância δ de O, e voa para o oeste, em direção a O, com
velocidade u também constante, conforme mostra a figura. Considerando t o instante em que a distância d
entre o helicóptero e o avião for mínima, assinale a alternativa correta.
a) A distância percorrida pelo helicóptero no instante em que o avião alcança o ponto O é δu/v.
b) A distância do helicóptero ao ponto O no instante t é igual a δv
v2  u2 .
c) A distância do avião ao ponto O no instante t é igual a δv 2  v 2  u2  .
d) O instante t é igual a δv  v 2  u2  .
e) A distância d é igual a δv v2  u2 .
08. Uma pequena bola de massa m é lançada de um ponto P contra uma parede vertical lisa com uma certa
velocidade v0, numa direção de ângulo α em relação à horizontal. Considere que após a colisão a bola retorna
3
Simulado Folião de Elite
ao seu ponto de lançamento, a uma distância d da parede, como mostra a figura. Nestas condições, o
coeficiente de restituição deve ser
a) e  gd  v02 sen2α  gd.
b) e  2gd  v02 cos2α  2gd.
c) e  3gd  2v02 sen2α  2gd.
d) e  4gd  v02 cos2α  gd.
e) e  2gd  v02 tan2α  gd.
09. Duas cargas pontuais q1  3,0 μC e q2  6,0 μC são colocadas a uma distância de 1,0 m entre si.
Calcule a distância, em metros, entre a carga q1 e a posição, situada entre as cargas, onde o campo elétrico é
nulo.
Considere kC = 9  109 Nm2/C2
a) 0,3
b) 0,4
c) 0,5
d) 0,6
e) 2,4
10. Na figura abaixo, está mostrada uma série de quatro configurações de linhas de campo elétrico.
4
Simulado Folião de Elite
Assinale a alternativa que preenche corretamente as lacunas da sentença abaixo, na ordem em que aparecem.
Nas figuras __________, as cargas são de mesmo sinal e, nas figuras __________, as cargas têm magnitudes
distintas.
a) 1 e 4 - 1 e 2
b) 1 e 4 - 2 e 3
c) 3 e 4 - 1 e 2
d) 3 e 4 - 2 e 3
e) 2 e 3 - 1 e 4
11. Um ciclista movimenta-se com sua bicicleta em linha reta a uma velocidade constante de 18 km/h. O pneu,
devidamente montado na roda, possui diâmetro igual a 70 cm. No centro da roda traseira, presa ao eixo, há
uma roda dentada de diâmetro 7,0 cm. Junto ao pedal e preso ao seu eixo há outra roda dentada de diâmetro
20 cm. As duas rodas dentadas estão unidas por uma corrente, conforme mostra a figura. Não há deslizamento
entre a corrente e as rodas dentadas. Supondo que o ciclista imprima aos pedais um movimento circular
uniforme, assinale a alternativa correta para o= número de voltas por minuto que ele impõe aos pedais durante
esse movimento. Nesta questão, considere   3 .
5
Simulado Folião de Elite
a) 0,25 rpm.
b) 2,50 rpm.
c) 5,00 rpm.
d) 25,0 rpm.
e) 50,0 rpm.
12. Uma partícula faz seguidos movimentos sobre o eixo horizontal OX , a partir da origem, exclusivamente
para a direita, convergindo, a cada deslocamento, para um ponto (XP,0) de onde essa partícula nunca passará,
como ilustrado na figura abaixo.¨
O tamanho de cada deslocamento, a partir do 2º, é a metade do deslocamento imediatamente anterior. Se
essa partícula leva 5 segundos para sair da origem O e chegar ao ponto (X P,0), sua velocidade média, em m/s,
é
a) 1,6
b) 1,4
c) 1,2
d) 0,8
e) 0,5
13. Em 1914, o astrônomo americano Vesto Slipher, analisando o espectro da luz de várias galáxias, constatou
que a grande maioria delas estava se afastando da Via Láctea. Em 1931, o astrônomo Edwin Hubble, fazendo
um estudo mais detalhado, comprovou os resultados de Slipher e ainda chegou a uma relação entre a distância
(x) e a velocidade de afastamento ou recessão (v) das galáxias em relação à Via Láctea, isto é, x  H01v . Nessa
relação, conhecida com a Lei de Hubble, H0 é determinado experimentalmente e igual a 75 km/(s.Mpc). Com o
auxílio dessas informações e supondo uma velocidade constante para a recessão das galáxias, é possível
calcular a idade do Universo, isto é, o tempo transcorrido desde o Big Bang (Grande Explosão) até hoje.
Considerando 1 pc = 3 x 1016 m, assinale a alternativa correta para a idade do Universo em horas.
a) 6,25 x 1017.
b) 3,75 x 1016.
c) 2,40 x1018.
d) 6,66 x 1015.
6
Simulado Folião de Elite
e) 1,11 x 1014.
14. Um bote de assalto deve atravessar um rio de largura igual a 800m, numa trajetória perpendicular à sua
margem, num intervalo de tempo de 1 minuto e 40 segundos, com velocidade constante.
Considerando o bote como uma partícula, desprezando a resistência do ar e sendo constante e igual a 6 m/s a
velocidade da correnteza do rio em relação à sua margem, o módulo da velocidade do bote em relação à água
do rio deverá ser de:
a) 4 m/s
b) 6 m/s
c) 8 m/s
d) 10 m/s
e) 14 m/s
15. Considere uma barra de liga metálica, com densidade linear de 2, 4  103 g / mm , submetida a uma variação
de temperatura, dilatando-se 3,0mm. Sabendo-se que o coeficiente de dilatação linear e o calor específico da
liga são, respectivamente, iguais a 2,0  105 º C1 e a 0,2cal / gº C , a quantidade de calor absorvida pela barra
nessa dilatação é igual, em cal, a
a) 72,0
b) 80,0
c) 120,0
d) 132,0
e) 245,0
16. Indique a alternativa que representa corretamente a tabela com os dados da posição, em metros, em
função do tempo, em segundos, de um móvel, em movimento progressivo e uniformemente retardado, com
velocidade inicial de valor absoluto 4 m/s e aceleração constante de valor absoluto 2 m/s2.
a)
0
1
2
3
s(m) 7
8
7
4
b)
s(m)
0
4
1
7
2
8
3
7
c)
s(m)
0
-4
1
-2
2
-4
3
-10
d)
s(m)
0
0
1
-3
2
-4
3
-3
e)
0
1
2
3
7
Simulado Folião de Elite
s(m)
0
4
7
8
17. Uma rampa para saltos de asa-delta é construída de acordo com o esquema que se segue. A pilastra de
sustentação II tem, a 0 °C, comprimento três vezes maior do que a I.
Os coeficientes de dilatação de I e II são, respectivamente, á1 e á2.
Para que a rampa mantenha a mesma inclinação a qualquer temperatura, é necessário que a relação entre á 1
e á2 seja:
a) á1 = á2
b) á1 = 2á2
c) á1 = 3á2
d) á2 = 3á1
e) á2 = 2á1
18. O gráfico a seguir mostra como variam as temperaturas de dois corpos, A e B, cada um de massa igual a
100 g, em função da quantidade de calor absorvida por eles.
Os calores específicos dos corpos A(cA) e B(cB) são respectivamente,
a) cA = 0,10 cal/g°C e cB = 0,30 cal/g°C
b) cA = 0,067 cal/g°C e cB = 0,20 cal/g°C
c) cA = 0,20 cal/g°C e cB = 0,60 cal/g°C
d) cA = 10 cal/g°C e cB = 30 cal/g°C
e) cA = 5,0 cal/g°C e cB = 1,7 cal/g°C
8
Simulado Folião de Elite
19. Um rapaz está em repouso na carroceria de um caminhão que desenvolve velocidade de 30 m/s. Enquanto
o caminhão se move para a frente, o rapaz lança verticalmente para cima uma bola de ferro de 0,10 kg. Ela
leva 1,0 segundo para subir e outro para voltar. Desprezando-se a resistência do ar, pode-se afirmar que a bola
caiu na(o):
a) estrada, a mais de 60 m do caminhão.
b) estrada, a 60 m do caminhão.
c) estrada, a 30 m do caminhão.
d) caminhão, a 1,0 m do rapaz.
e) caminhão, na mão do rapaz.
20. Em um recipiente, de paredes adiabáticas e capacidade térmica desprezível, introduzem-se 200 g de
água a 20 °C e 80 g de gelo a - 20 °C. Atingindo o equilíbrio térmico, a temperatura do sistema será
Dados:
calor específico da água = 1,0 cal/g°C
calor específico do gelo = 0,50 cal/g°C
calor latente de fusão de gelo = 80 cal/g
a) - 11 °C
b) 0 °C, restando 40 g de gelo.
c) 0 °C, restando apenas água.
d) 0 °C, restando apenas gelo.
e) 11 °C
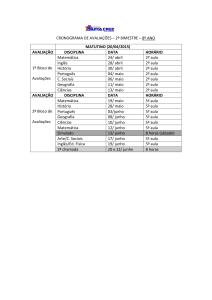
MATEMÁTICA
01. Na tabela de 8 colunas e infinitas linhas numeradas, indicada na figura, podemos formar infinitos
quadrados coloridos 3  3, como mostra um exemplo.
Nessa tabela, o quadrado colorido 3  3 cuja soma dos 9 elementos é igual a 4.806 ocupa três linhas, sendo
uma delas a linha
a) 71.
b) 67.
c) 53.
d) 49.
e) 41.
02. O número de soluções da equação (1  sec θ)(1  cossec θ)  0, com θ  [π, π], é
a) 0.
b) 1.
9
Simulado Folião de Elite
c) 2.
d) 3.
e) 4.
03. O quadrado PQRS está inscrito em um círculo de centro C. A corda intersecta a diagonal do quadrado em
A, sendo que QA  6 cm e AB  4 cm.
Nas condições descritas, a medida do lado do quadrado PQRS, em cm, é igual a
a) 2 10.
b) 5 2.
c) 2 15.
d) 6 2.
e) 7 2.
04. Sejam 1, 2, ... , 100 os lados dos quadrados Q1, Q2, ... , Q100 , respectivamente.
Se 1  1 e k  2 k 1, para k  2, 3, ... , 100, a soma das áreas desses quadrados é igual a
a)
b)
c)
d)
e)
3 99
4
4
1 99
4
4
1 100
 (4
 1)
3
1 100
4
3
1 100
4
1
3
05. Na figura, o retângulo ABCD tem lados de comprimento AB  4 e BC  2. Sejam M o ponto médio do lado
BC e N o ponto médio do lado CD. Os segmentos AM e AC interceptam o segmento BN nos pontos E e F,
respectivamente.
10
Simulado Folião de Elite
A área do triângulo AEF é igual a
a)
b)
c)
d)
e)
24
25
29
30
61
60
16
15
23
20
06. No esquema abaixo, estão representados um quadrado ABCD e um círculo de centro P e raio r, tangente
às retas AB e BC. O lado do quadrado mede 3r.
A medida θ do ângulo CAP pode ser determinada a partir da seguinte identidade trigonométrica:
tg(α  β) 
tg(α )  tg(β)
1  tg(α )  tg(β)
O valor da tangente de θ é igual a:
a) 0,65
b) 0,60
c) 0,55
d) 0,50
e) 0,75
07. Seja Pn um polígono convexo regular de n lados, com n  3. Considere as afirmações a seguir:
I. Pn é inscritível numa circunferência.
II. Pn é circunscritível a uma circunferência.
11
Simulado Folião de Elite
III. Se
n
é o compromisso de um lado de Pn e an é o comprimento de um apótema de Pn , então
an
 1 para
n
todo n  3.
É (são) verdadeira(s)
a) apenas I.
b) apenas II.
c) apenas III.
d) apenas I e II.
e) I, II e III.
08. Calcule o valor da expressão :
.
a)0
b)1
c)1/2
d)1/3
e)
09. No intervalo [0,
a equação sen 4(x) + cos 4(x) =
possui soma dos inversos das raízes igual à:
a)15/2
b)117/10
c)15/
d)2
e)117/5
10. Em um triângulo ABC , temos: 3 sen(A) + 4 cos(B)=6 e 4 sen(B)+3cos(A) = 1
Calcule o valor do ângulo C :
a)45°
b)60°
c)30°
d)90°
e)120°
.
11. Seja z um número complexo tal que
é:
a)
b) /2
c)2
d)
e)2
12. O valor de
, onde
no sistema:
12
é o conjugado de z. O módulo do complexo
Simulado Folião de Elite
a)29
b)30
c)31
d)35
e)36
13. Sejam W=
para o qual W
a){1
9}
b){
9}
c){6
9}
d){
6}
e)
. Qual é o conjunto dos valores de k
e
14. Listando-se em ordem crescente todos os números de 5 dígitos distintos, formados com os elementos do
conjunto {1,2,4,6,8} o número 62417 ocupa o n-ésimo lugar. O valor de n vale:
a)79
b)80
c)81
d)82
e)83
15. Se tg(x)+sec(x)=7/5, o valor de sen(x) + cos(x) vale:
a)47/37
b)12/37
c)37/47
d)18/47
e)40/47
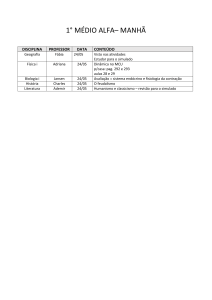
16. Um fisioterapeuta elaborou o seguinte plano de treinos diários para o condicionamento de um maratonista
que se recupera de uma contusão:
- primeiro dia – corrida de 6 km;
- dias subsequentes - acréscimo de 2 km à corrida de cada dia imediatamente anterior.
O último dia de treino será aquele em que o atleta correr 42 km.
O total percorrido pelo atleta nesse treinamento, do primeiro ao último dia, em quilômetros, corresponde a:
a) 414
b) 438
c) 456
d) 484
e) 490
17. Izidoro, Mariane e Camila foram convidados a fazerem afirmações sobre o número N  250  420.
13
Simulado Folião de Elite
- Izidoro afirmou que N é múltiplo de 8;
- Mariane afirmou que metade de N é igual a 225  410 ;
- Camila afirmou que N é par.
Quantas das afirmações feitas pelos participantes são verdadeiras?
a) 0
b) 1
c) 2
d) 3
e) 7
18. Simplificando a expressão
a4  b4  ab3  a3b  ab2  a2b
a2  b2
a
b
ab
b)
ab
a)
a3  ab  b3
ab
3(a ab  b)
d)
ab
c)
e) 1
19. O valor de
é:
a)0
b)-2/3
c)-1
d)2/3
e)1
20. Dado que :
Qual o valor de n?
a)21
b)22
c)23
d)24
e)25
14
, a  b, obtém-se:
Simulado Folião de Elite
Gabarito de Física
Resposta da questão 1:
[C]
A figura mostra o movimento do corpo:
Aplicando Torricelli, vem:
V 2  V02  2aΔS  0  402  2x10x0,8H  16H  1600  H  100m .
Resposta da questão 2:
[A]
Analisando o movimento do automóvel conforme a figura abaixo, temos que:
 v1

1 t1  t
 ΔS  4 m
 1
v 2

2 t2  t  4
 ΔS  16 m
 1
Assim, podemos encontrar expressões matemáticas que representam as velocidades nos dois instantes.
Analisando do instante 0 ao instante 1, temos que:
v12  v 02  2  a  ΔS1
v1  2  a  ΔS1
Analisando do instante 0 ao instante 2, temos que:
v 22  v 02  2  a  ΔS2
v 2  2  a  ΔS 2
15
Simulado Folião de Elite
Se v 2  v1  a  Δt , onde Δt  t 2  t1  4 s .
2  a  ΔS2  2  a  ΔS1  a  Δt
a  Δt  2  a  ΔS2  2  a  ΔS1
a  Δt  2  a 

ΔS2  ΔS1

Elevando ao quadrado ambos os lados e substituindo os valores, temos que:
a 2  42  2  a 

4  16
16  a  2   2  4 
a

2
2
8
16
a  0,5 m s2
Resposta da questão 3:
[C]
Temos que a força resultante sobre a carga elétrica é a soma vetorial das contribuições do campo elétrico e do campo magnético. Como
os campos e a direção de movimento da partícula são perpendiculares entre si e a partícula desenvolve um movimento retilíneo
uniforme na região dos campos elétrico e magnético, então a resultante das forças elétrica e magnética é nula.
As únicas possibilidades para que a Força resultante seja igual a zero, considerando a partícula com carga positiva ou negativa são
mostradas na figura abaixo:
FR  0
E usando as definições das forças elétrica e magnética:
Fe  Eq
Fm  qvB
Ficamos com:
Fe  Fm
Assim,
Eq  qvB
E a velocidade da partícula é determinada:
v
E
1,0  103 V / m
v
 v  1,0  104 m / s
B
0,1 T
16
Simulado Folião de Elite
Resposta da questão 4:
[E]
Lembrando,
- Cargas Positivas  Campo Elétrico Divergente
- Cargas Negativas  Campo Elétrico Convergente
Adotando,
Q1  4q
Q2  2q
Antes de qualquer análise numérica, se faz necessário uma análise quanto as possibilidades de se ter um campo elétrico nulo nesta
situação.
1. Em um ponto a esquerda da carga Q1, o campo elétrico nunca será nulo, pois o módulo de Q1 é maior que o de Q2 e a distância de
Q1 sempre será menor que a de Q2 .
2. Em um ponto entre Q1 e Q2 , os campos elétricos irão se somar, portanto este nunca será nulo.
3. Em um ponto a direita de Q2 , é possível se ter um ponto em que o campo elétrico resultante seja nulo.
Desta forma, para que o campo elétrico seja nulo, o campo elétrico gerado por Q1 tem que ser igual ao campo elétrico gerado por Q2 :
E1  E2
kQ1
d12
4q
x
2
2
x
2



kQ2
d22
2q
 x  d 2
1
2
x  2dx  d2
2x 2  4dx  2d2  x 2
x 2  4dx  2d2  0
Resolvendo a equação, obtém-se as seguintes respostas:


2  d2  2 
x '  2d  d 2  d 2  2
x ''  2d  d


Nota-se que x’’ é um ponto a esquerda da carga Q1, não sendo uma resposta factível. Logo, a única resposta é x '  d 2  2 .
Resposta da questão 5:
[C]
Dados: α  5π  104 C1; L0  2 m  200 cm; R  30 cm; Δθ  30  π 6 rad.
A figura ilustra a situação.
17
Simulado Folião de Elite
Analisando a figura, nota-se que, quando o disco gira de um ângulo Δθ, não havendo escorregamento entre ele e a barra, o ponto P do
disco sofre um correspondente deslocamento angular igual a a. Em relação ao centro do cilindro, a extremidade livre da barra também
avança uma distância igual a a.
Usando a definição de ângulo em radiano:
a
π
a
Δθ   
 a  5 π cm.
R
6 30
Como também não há escorregamento entre o disco e o piso, o ponto Q do disco também sofre um deslocamento angular igual a a.
Assim, como ilustra a figura, em relação à parede, a extremidade livre da barra avança:
ΔL  2 a  2(5π)  ΔL  10 π cm.
Aplicando a expressão da dilatação linear:
ΔL
10 π
ΔL  L0 α ΔT  ΔT 
 T  25 

L0 α
200  5 π  104
T
105
103
 25  100  25 
T  125 °C.
Nota: Se o disco não estivesse apoiado sobre o piso, mas apoiado sobre seu próprio eixo, fixo em relação a parede, não haveria
movimento de translação, apenas de rotação, como indicado na figura a seguir.
Então:
18
Simulado Folião de Elite
ΔL  a  5π cm.
Assim:
ΔL  L0 α ΔT  ΔT 
T
1
2  102
ΔL
5π
 T  25 

L0 α
200  5 π  104
 25  50  25 
T  75 °C.
Que é a reposta [B] dada pelo gabarito oficial.
Resposta da questão 6:
[D]
A velocidade resultante da imagem é a soma vetorial das velocidades devido aos movimentos do espelho e do objeto.
- Se o espelho gira com velocidade angular
ω, a imagem gira com o dobro dessa velocidade
(2ω), no mesmo sentido, com velocidade linear, v1  2 ω d.
- Se o objeto se desloca com velocidade v, a imagem desloca-se com velocidade de mesmo módulo, mantendo-se simétrica do objeto
em relação ao espelho | v 2 | v.
O enunciado não especifica o referencial adotado, portanto será considerado um referencial fixo no solo.
Assim:
- A velocidade escalar da imagem é máxima quando v1 e v 2 têm mesmo sentido:
vmáx  v1  v2  vmáx  2 ω d  v.
- A velocidade escalar da imagem é mínima quando v1 e v 2 têm sentidos opostos:
vmín  v1  v2  vmín  2 ω d  v .
As figuras ilustram as duas situações, mostrando que, para satisfazer as condições de velocidade máxima e mínima, a velocidade do
objeto deve ter direção tangente à circunferência com centro no ponto P e raio d.
Resposta da questão 7:
[C]
19
Simulado Folião de Elite
A figura mostra a trajetória seguida pelo helicóptero em relação ao avião. Note que os triângulos, sombreado e OPQ, são semelhantes,
portanto:
OQ u
δu

 OQ 
δ
w
w
Tempo decorrido até o instante em que a distância é mínima t 
Durante o tempo acima o avião voa ΔS  ut 
OQ δu

w
w2
δu2
w2
Portanto, a distância do avião ao ponto O será:
x  δ
δu2
w2

δ(w 2  u2 )
w2

δv 2
u2  v 2
Resposta da questão 8:
[A]
Num lançamento oblíquo sobre superfície plana e horizontal, sendo desprezível a resistência do ar, o tempo total de movimento (tT) e a
altura máxima atingida (H), dependem somente da componente vertical de velocidade (v0y = v0 sen ). Como se pode demonstrar:
2 v 0 sen α
2 v 0y


.
t T 
g
g


2
v 02 sen2α
v 0y


.
H 
2g
2g

Numa situação hipotética, se, ao longo do movimento, somente houvesse redução na componente horizontal da velocidade (vx), seria
alterado apenas o alcance horizontal (A), como indicado na figura.
20
Simulado Folião de Elite
No caso dessa questão, como a parede é lisa, não ocorre alteração na componente vertical da velocidade, portanto o tempo total de
movimento é igual ao tempo total que seria gasto se não houvesse o choque. O tempo t1 do lançamento até o choque é maior que o
tempo t2 do choque ao retorno ao solo, pois o choque ocorre antes do ponto mais alto da trajetória.

d
d  v x t1  t1 
vx


d

'
d  v x t 2  t 2  '
vx


t1  t 2  t T  2 v 0 sen α

g
d
v 'x

2 v 02 senα cos α  g d
g v 0 cos α

2 v 0 sen α
d
d


v x v 'x
g

v 2 sen 2α  g d
d g v 0 cos α
 0
 v 'x 
'
2
g v 0 cos α
vx
v 0 sen 2α  g d

d
O coeficiente de restituição (e) é definido como:
g d v0 cos α
e
e
v afast
v aprox

v 'x
vx
 e
gd
v 02
sen 2 α  g d
v 02
sen 2 α  g d
v0 cos α

.
Resposta da questão 9:
[B]
21
d
v 'x

2 v 0 sen α
d


g
v 0 cos α
Simulado Folião de Elite
Observe a figura abaixo.
Para que o campo elétrico no ponto assinalado seja nulo, E1  E2 . Portanto:
kq1
x
2

kq2
2
(1  x)

3
x
2

6
2
(1  x)
1

x
2

2
1  2x  x 2
2x 2  x 2  2x  1  x 2  2x  1  0
 2  2 2  4x1x (1)  2  8  2  2 2
x


 2  1  0,4m
2
2
2
Resposta da questão 10:
[A]
Na figura 1 as linhas de força emergem das duas cargas, demonstrando que elas são positivas. Observe que o número de linhas de força
emergente da carga da direita é maior do que as que “morrem” na carga da esquerda evidenciando que o módulo da carga da direita é
maior
Na figura 2 as linhas de força emergem da carga da esquerda (positiva) e “morrem” na carga da direita (negativa). Observe que o
número de linhas de força “morrendo” na carga da direita é maior do que as que emergem da carga da esquerda evidenciando que o
módulo da carga da direita é maior
Na figura 3 as linhas de força emergem da carga da esquerda (positiva) e “morrem” na carga da direita (negativa). Observe que o
número de linhas de força “morrendo” na carga da direita é igual àquele do que as que emergem da carga da esquerda evidenciando que
os módulos das cargas são iguais.
Na figura 4 as linhas de força emergem de ambas as cargas evidenciando que elas são positivas. Observe que o número de linhas de
força que emergem das cargas é igual evidenciando que os módulos das cargas são iguais.
Resposta da questão 11:
[E]
A figura abaixo mostra os diversos componentes do mecanismo e suas dimensões.
22
Simulado Folião de Elite
Denominemos Ω a velocidade angular da coroa e ω a velocidade angular da catraca e consequentemente da roda, já que elas rodam
solidárias.
Como a coroa e a catraca são interligadas por uma correia podemos dizer que as velocidades lineares de suas periferias são iguais.
ωr
Vcoroa  Vcatraca  ΩR  ωr  Ω 
(01)
R
D
2V
Por outro lado a velocidade da bicicleta pode ser calculada por: V  ω  ω 
(02)
2
D
Substituindo 02 em 01, vem:
2Vr
Ω
(03)
RD
V =18km/h = 5,0m/s
D= 70cm = 0,7m
2R = 20cm  R = 0,1m
2r = 7cm  r = 0,035m
Substituindo os valores em 03, temos:
5
rot
2.5.0,035
5
2
Ω
 5,0rd / s  Ω  5,0rd / s  π
  60  50RPM
1
0,1 0,7
6
min
60
Resposta da questão 12:
[A]
ΔS  4  2  1  0,5  ...........
Progressão geométrica ilimitada de razão 0,5, em que o primeiro termo é 4.
ΔS  lim S 
n
Vm 
a1
4

 8,0m
1  q 1  0,5
ΔS 8
  1,6m / s .
Δt 5
Resposta da questão 13:
[E]
75  103 m
 25  1019 s1
6
16
1s.10 .3.10 m
1
4  1017
17
x  H01v  v.t  t  H01 

4

10
s

h  1,1 1014 h
3600
25  1019
H0  75km / (s.Mpc) 
23
Simulado Folião de Elite
Resposta da questão 14:
[D]
A figura mostra as velocidades do barco em relação ao rio, do rio em relação à margem e a resultante das duas.
VRe sul tan te 
ΔS 800

 8,0m / s
Δt 100
Aplicando Pitágoras ao triângulo sombreado, vem:
VB2  82  62  100  VB  10m / s
Resposta da questão 15:
[A]

m
L0
Q  mc
Q
Q
0,2
m c
c
 2,4 x10 3 x

 Q  72cal
 . 

3
L  L 0 .. L L 0 
2x10 5

Resposta da questão 16:
[B]
O gráfico baixo mostra a variação da velocidade e os deslocamentos a cada segundo.
Percebemos que os deslocamentos calculados estão melhor representados na opção B.
Resposta da questão 17:
[C]
24
Simulado Folião de Elite
Para manter a mesma inclinação, as dilatações devem ser iguais, portanto:
L1  L1
L1.1.  L 2 . 2 .
L1.1  3L1. 2
1  3 2
Resposta da questão 18:
[A]
Resposta da questão 19:
[E]
Resposta da questão 20:
[B]
Gabarito de Matemática
01. [B]
02. [A]
03. [C]
04. [C]
05. [D]
06. [B]
07. [D]
08. [B]
09. [B]
10. [C]
11. [D]
12. [C]
13. [C]
14. [C]
15. [A]
16. [C]
17. [C]
18. [C]
19. [E]
20. [B]
25