www.ifrs.bento.edu.br Criado por: Marcos Pinheiro de Lima Mini

Mini Curso GeoGebra
Etapa I:
 Apresentação do Software;
O GeoGebra é um software dinâmico, muito usado em conteúdos de Geometria,
Álgebra, Estatística e Cálculo. É um programa livre e de código aberto; de interface fácil
de usar, mas com poderosos recursos; gráficos, tabelas e álgebra são conectadas
dinamicamente; ferramentas de autoria para criar ferramentas de ensino interativo
exibidos como páginas da internet; e a destacável percepção dupla dos objetos: cada
expressão destacada na Janela Algébrica corresponde um objeto na Janela Gráfica e viceversa.
 Download do GeoGebra: http://www.geogebra.org/cms/pt_BR/download; Java:
http://www.java.com/pt_BR/download/;
Etapa II:
Campo de Entrada:
Ponto: A = (x,y)
Segmento: Segmento[A,B] ou Segmento[(x,y) , (x’,y’)]
Reta: Reta[A,B] ou Reta[(x,y), (x’,y’)]
Mediatriz: Mediatriz[A,B] ou Mediatriz[Segmento[A,B]]
Bissetriz: Bissetriz[a,b]
Seletor: a = constante
Ponto Médio: Pontomédio[A,B] ou Pontomédio[a]
Interseção: Interseção[a,b]
Extremidade de uma função: Extremo[f(x)]
Raizes de uma função: Raiz[f(x)]
*
Multiplicação
/
Divisão
^
Potência
www.ifrs.bento.edu.br
Criado por: Marcos Pinheiro de Lima
^(1/2) ou sqrt( )
Raiz Quadrada
+
Soma
-
Subtração
sin ( )
Seno
cos( )
Cosseno
tan( )
Tangente
log( ) ou ln( )
Logaritmo (base e)
lg ( )
Logaritmo (base 10)
ld( )
Logaritmo (base 2)
Desenvolvimento de atividades para fixação das ferramentas;
- Construir duas retas paralelas.
- Construir dois segmentos de retas com ângulo de 45º entre elas.
- Construir duas retas perpendiculares.
- Construir a mediatriz de um segmento AB. (Reta perpendicular ao segmento passando pelo
seu ponto médio).
- Construir a bissetriz de um ângulo AOB. (Reta que divide o ângulo em dois ângulos
congruentes).
- Construir um círculo de centro O (ponto qualquer) e raio 5.
- Construir um seletor “a” de mínimo 1, máximo 5 e de incremento 1. Após construa um
circulo dado o raio “a”. Note que se você variar o seletor, o tamanho de seu raio variará
conforme o seletor.
- Construa um círculo de centro C(-2,-3) e raio 3. Calcule a área deste círculo e o
comprimento do círculo.
III Etapa:
www.ifrs.bento.edu.br
Criado por: Marcos Pinheiro de Lima
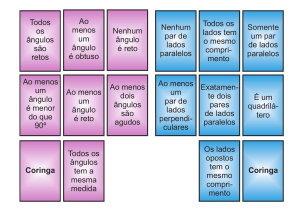
Construa as formas geométricas, de maneira que, aos manipularmos os pontos,
mantenha suas propriedades:
- Construir um triângulo isósceles. Propriedades: Dois lados com a mesma medida.
- Construir um triângulo eqüilátero. Propriedades: Três lados de medidas iguais.
- Construir um triângulo retângulo. Propriedades: Um de seus ângulos internos reto (90º).
- Construir um retângulo. Propriedades: Quadrilátero de quatro ângulos internos reto (90º) e
de lados opostos iguais.
- Construir um losango. Propriedades: Quadrilátero de quadro lados iguais e ângulos opostos
iguais.
- Construir um quadrado. Propriedades: Quadrilátero com quatro lados congruentes e quatro
ângulos internos reto (90º).
- Construir um trapézio. Propriedades: Quadrilátero com apenas dois lados opostos paralelos.
Tarefas Extras (detalhadas):
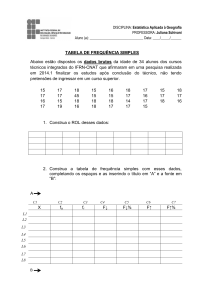
1. Representar graficamente uma função num intervalo de domínio e algumas
propriedades.
Para representarmos uma função definida pela sua expressão analítica num dado
intervalo,
basta
usarmos
o
seguinte
comando:
Função[<expressão_da_função>,<x_incial>,<x_final>]
 Representar a função definida por f(x) = x² - 4 no intervalo [-2,3].
a. Para representar recorra ao comando: Função[x^2-4, -2,3]
b. Represente graficamente os zeros da função através da ferramenta (intersecção) ou
do comando: Raiz[f]
c. Represente graficamente o mínimo da função através do comando: Extremo[f].
www.ifrs.bento.edu.br
Criado por: Marcos Pinheiro de Lima
2. Contrua uma roda gigante, de maneira que anime-a.
a.
b.
c.
d.
Construa um seletor, ângulo de mínimo 0º e máximo 360º, incremento de 1.
Construa um círculo dado o centro e raio 5.
Faça um ponto em qualquer posição sobre a circunferência.
Usando a ferramenta ângulo com amplitude fixa (α) sobre este ponto criado e o
centro da circunferência, será criado outro ponto de amplitude α em relação ao
ponto pertencente à circunferência.
e. Construa outros pontos sequêncialmente (sempre em relação aos novos pontos
criado), usando a ferramenta ângulo com amplitude fixa (30º).
f. Construa em cada ponto pertencente à circunferência, circulo dados o centro e raio
(0.5).
g. Construa sobre estes circulos, setores circuncirculares dados três pontos,
formando sobre estes círculos uma boca de aproximadamente 90º.
h. Finalizando a tarefa, clique com o botão direito do mouse sobre o seletor e
selecione a opção animação ativada.
DESAFIO:
1. Construa um Tangran
www.ifrs.bento.edu.br
Criado por: Marcos Pinheiro de Lima
www.ifrs.bento.edu.br
Criado por: Marcos Pinheiro de Lima