Leis de Kirchoof (Nós e Malhas)

CEFETES
Escola Técnica Federal do Espírito Santo
Tecnológico em Eletromecânica
Leis de Kirchoof


Eletricidade
Professor Luis Alberto
Pag1
http://geocities.yahoo.com.br/luisarquivos
(Nós ou Correntes e Malhas ou Tensões)
As leis são utilizadas para a resolução de circuitos, determinando os valores de Correntes (amper) e Tensões (volts) nos componentes do
circuito.
Técnica de Análise de um circuito :
o
Nó : é o ponto de conexão física (junção) entre dois o mais condutores ou entre dos ou mais componentes elétricos.
o
Braço ou ramo : è a parte do circuito que liga dois nós consecutivos e os elementos estão em serie.
o
Malha : Um percurso o caminho qualquer fechado, sobre o diagrama do circuito, que se inicia num Nó qualquer e termina no mesmo
nó.
o
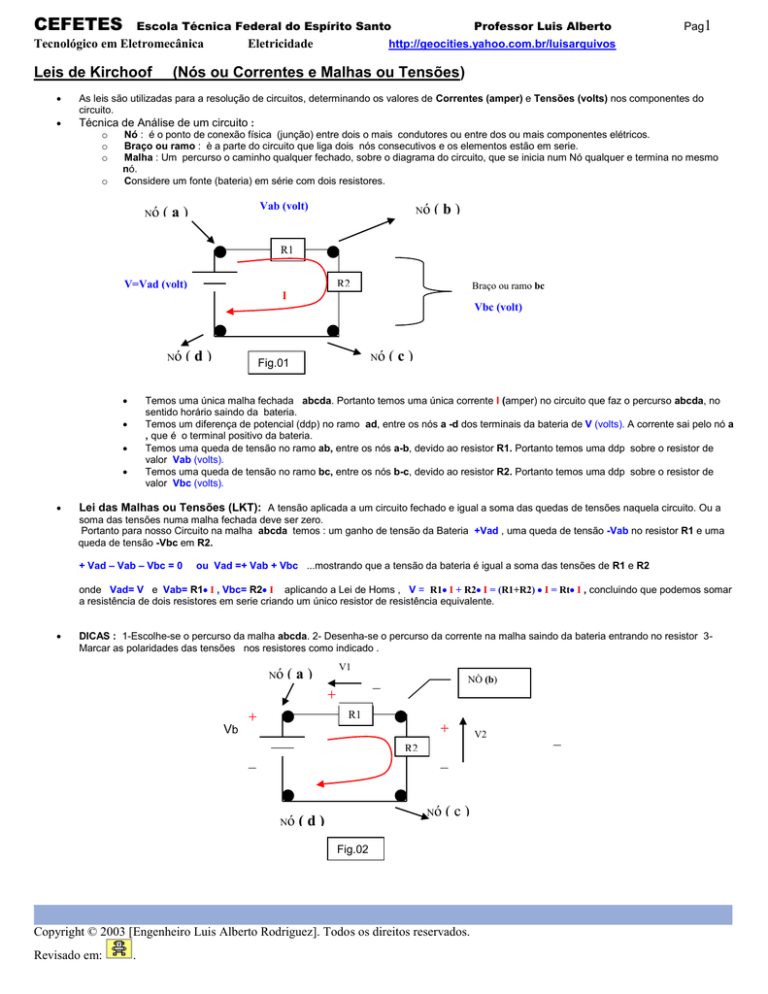
Considere um fonte (bateria) em série com dois resistores.
Nó
Vab (volt)
(a)
Nó
(b)
R1
R2
V=Vad (volt)
Braço ou ramo bc
I
Vbc (volt)
Nó

Nó
Fig.01
(c)
Temos uma única malha fechada abcda. Portanto temos uma única corrente I (amper) no circuito que faz o percurso abcda, no
sentido horário saindo da bateria.
Temos um diferença de potencial (ddp) no ramo ad, entre os nós a -d dos terminais da bateria de V (volts). A corrente sai pelo nó a
, que é o terminal positivo da bateria.
Temos uma queda de tensão no ramo ab, entre os nós a-b, devido ao resistor R1. Portanto temos uma ddp sobre o resistor de
valor Vab (volts).
Temos uma queda de tensão no ramo bc, entre os nós b-c, devido ao resistor R2. Portanto temos uma ddp sobre o resistor de
valor Vbc (volts).




(d)
Lei das Malhas ou Tensões (LKT): A tensão aplicada a um circuito fechado e igual a soma das quedas de tensões naquela circuito. Ou a
soma das tensões numa malha fechada deve ser zero.
Portanto para nosso Circuito na malha abcda temos : um ganho de tensão da Bateria +Vad , uma queda de tensão -Vab no resistor R1 e uma
queda de tensão -Vbc em R2.
+ Vad – Vab – Vbc = 0
ou Vad =+ Vab + Vbc ...mostrando que a tensão da bateria é igual a soma das tensões de R1 e R2
onde Vad= V e Vab= R1 I , Vbc= R2 I aplicando a Lei de Homs , V = R1 I + R2 I = (R1+R2)  I = Rt I , concluindo que podemos somar
a resistência de dois resistores em serie criando um único resistor de resistência equivalente.

DICAS : 1-Escolhe-se o percurso da malha abcda. 2- Desenha-se o percurso da corrente na malha saindo da bateria entrando no resistor 3Marcar as polaridades das tensões nos resistores como indicado .
Nó
V1
(a)
_


NÒ (b)
R1

Vb
R2
_
_
Nó
Nó
(d)
(c)
Fig.02
Copyright © 2003 [Engenheiro Luis Alberto Rodriguez]. Todos os direitos reservados.
Revisado em:
.
V2
_
CEFETES
Escola Técnica Federal do Espírito Santo
Tecnológico em Eletromecânica

Eletricidade
Professor Luis Alberto
Pag2
http://geocities.yahoo.com.br/luisarquivos
Leis dos Nos ou das Correntes (LKC) : A soma das correntes que entram em um Nó é igual a soma das correntes que saem
do mesmo Nó. Considerar que as correntes que entram no Nó são positivas (+) e as que saem como negativas.
I1=I2 +I3
I2
I1
I3
Fig.03
Podemos dizer que a soma algébrica de todas as correntes no Nó é igual a zero: (=símbolo sigma=somatória) ,
  =0 , +1 - 2 - 3= 0
R2
R1
R2
I1
I2
I2
R1
R3
I3
I1
R3
I3
Fig.05
Fig.04
Exercício 1: (LKT) Resistores em Serie
Considere que a bateria tenha Vb= 24volt, R1= 10 (ohms), R2= 20 (ohms). Por LKT e Lei de Ohms ,calcule : corrente, V1,V2 e comprove
que a resistência equivalente é dada por Req.=R1+R2.
Nó
V1
(a)
_


Nó
R1

Vb
V2
R2
_
_
I
Nó
Solução:
(b)
Nó
(d)
Vb-V1-V2=0 , Vb= V1+v2 , V1=R1*I1 , V2=R2*I2
I=I1=I2 , Vb=( R1* I )+(R2*I)=(R1+R2)*I.
Req.=(R1+R2)
I=Vb / (R1/R2)= 24 volt /(10+20) ohms = 0,8 amper
V1=R1 * I =10 (ohms) * 0,8 (amper) = 8volt
V2=R2 * I = 20 (ohms) * 0,8 (amper)= 16 volt
Comprovando LKT : Vb = V1+V2 = 8 volt + 16 volt = 24 volt
(c)
Exercício 2: (LKC) Resistores em paralelo
Considere que a bateria tenha Vb= 24volt, R1= 10 (ohms), R2= 20 (ohms). Por LKC e Lei de Ohms ,calcule : correntes, V1,V2 e
comprove que a resistência equivalente é dada por Req.= (R1*R2) / (R1+R2).
Solução :
bV
It
R1
I1
+
- V1
I2
R2
+
-
O sentido da corrente arbitra-se como mostrado na figura, podendo
ser outros sentidos. It – I1 –I2 = 0 , It = +I1 + I2 ,
V2
Vb = V1 = V2 , I1=V1/R1 = Vb/R1 , I2=V2/R2 = Vb/R2 ,
It= I1+I2= Vb/R1 + Vb/R2 = (1/R1 + 1/R2 ) * Vb = (1/10 ohms
+1/20 ohms )*24volts = 3,6 amper.
(1/R1 + 1/R2)= 1/Req. = (R1+R2)/(R1*R2) logo Req=
(R1*R2)/(R1+R2) = (10*20)/(10+20)= 6,67 ohms.
It= 3,6 amper ; I1=Vb/R1=24volt / 10 ohms =2,4 amper ;
I2=Vb/R2=24volt/20ohms=1,2 amper.
Copyright © 2003 [Engenheiro Luis Alberto Rodriguez]. Todos os direitos reservados.
Revisado em:
.
CEFETES
Escola Técnica Federal do Espírito Santo
Tecnológico em Eletromecânica
Eletricidade
Professor Luis Alberto
Pag3
http://geocities.yahoo.com.br/luisarquivos
Exercício 3: (LKC) e LKT Resistores em paralelo e serie
Solução : LKC
Vb
R1
R2
I1
I2
O sentido da corrente arbitra-se como mostrado na figura.
I1-I2-I3 =0 ; I1=I3 + I2 ; I1= v1/R1 ; I2=V2/R2 ; I3=V3/R3
V1/R1=V2/R2 +V3/R3 ; V2=V3=V ; V1/R1= V*(1/R2+1/R3) =I1
(1/R1 +1/R3) = 1/Req. ; Req= (R1*R2)/(R1+R2)
Vb – V1- V=0 ; Vb – R1*I1 – Req.*I1=0 ; Vb - (R1+Req)*I1 =0;
I1= Vb / (R1+Req) ; V1= I1 * R1 ; V= I1 * Req=V1=V2 ;
I2= V/R2 , I3= V/R3
R3
I3
+
-
(a)
(b)
+
R1
Vb
I1
R2
I2
+
R3
+
I3
(e)
-
(d)
(c)
Solução : LKT
Escolhese a Malha 1 : abdea ; Malha2 : bcdb . O sentido da
corrente arbitra-se como mostrado na figura.
Polarizar os resistores.
Malha1: Vb – V1 –Vbc +Vdb =0 ; Vb - R1*I1 –R3*I1 + R3*I2 =0 ; Vb –
(R1+R3)*I1 +R3*I2 =0
Malha2 : -Vdb+Vbc –V2 =0 ; -R3*I2 +R3*I1 – R2*I2 =0 ; -(R3+R2)*I2 +
R3*I1 =0 ;
Logo duas equações e duas incognitas: acha-se I1 e I2
Vb – (R1+R3)*I1 +R3*I2 =0
-(R3+R2)*I2 + R3*I1 =0
Achar I3= I1-I2 ; Com I1 ,I2, I3 calculados achar
V1,V2,V3 usando Lei de Ohms.
Copyright © 2003 [Engenheiro Luis Alberto Rodriguez]. Todos os direitos reservados.
Revisado em:
.