2º Lista Resolvida.

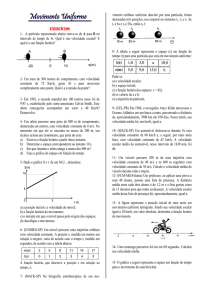
1) Um carro desloca-se em uma trajetória retilínea descrita pela função
S=20+5t (no SI). Determine:
A função horária no movimento uniforme é dada como: S = S0 + V * T.
a) a posição inicial;
S0 = 20 m (no S.I. – sistema internacional de unidades).
b) a velocidade;
V = 5 m/s
c) a posição no instante 4s;
S = S0 + V * T => S = 20 + 5 * 4
vale => S = 40 metros
=> A posição S no tempo de 4 segundos
d) o espaço percorrido após 8s;
A função horária informa a posição do carro em função do tempo, assim podemos
calcular a posição no instante de 8 segundos subtraindo a posição inicial para saber
qual o espaço percorrido pelo carro, assim temos:
S(8s) = S0 + V * T => S(8s) = 20 + 5 * 8 = 60 metros é a posição do carro.
∆S = Sf – Si = 60 – 20 = 40 metros. A distância percorrida foi de 40 metros.
e) o instante em que o carro passa pela posição 80m;
A função horária informa a posição do carro em função do tempo decorrido S = S0
+ V * T, assim temos que S = 80 = 20 + 5 * T, isolando o Tempo T, temos:
80 = 20 + 5 * T => 80 – 20 = 5 * T => T = 60 / 5 = 12 segundos. O instante
que o carro passa pela posição 80 metros é de 12 segundos.
f) o instante em que o carro passa pela posição 20m.
A função horária informa a posição do carro em função do tempo decorrido S = S0
+ V * T, assim temos que S = 20.
20 = 20 + 5 * T => 20 – 20 = 5 * T => T = 0 segundos, ou seja, o instante em
que o carro passa pela posição 20 metros é o instante inicial de 0 segundos.
2) Em um trecho de declive de 10km, a velocidade máxima permitida é de
70km/h. Suponha que um carro inicie este trecho com velocidade igual a
máxima permitida, ao mesmo tempo em que uma bicicleta o faz com
velocidade igual a 30km/h. Qual a distância entre o carro e a bicicleta
quando o carro completar o trajeto?
A função horária informa a posição do carro em função do tempo decorrido,
supondo que o carro inicie este trecho com velocidade de 70 km/h e se mantenha
constante, temos que a velocidade média é de 70 km/h e a função horária S = S0 +
V * T (S0=0) => S = V * T => S = 70 * T.
A função horária da bicicleta é: S = S0 + V * T (S0) => S = 30 * T.
O carro irá completar o trajeto quando percorrer os 10 km de declive com
velocidade de 70 km/h, assim temos:
∆
= ∆ => 70= ∆ => ∆ ∗ 70 = 10 => ∆ =
= 0,14ℎ
O carro completará o percurso em 0,14h então utilizando este tempo na função
horária da bicicleta, teremos a posição em que ela se encontra quando o carro
terminar de percorrer os 10 km.
A função horária da bicicleta é: S = S0 + V * T (S0) => S = 30 * 0,14 = 4,2 km.
A bicicleta estará na posição 4,2 km e o carro estará na posição de 10 km. Assim, a
distância entre o carro e a bicicleta quando o carro terminar o trajeto vale 10 – 4,2
= 6,8 km de distância.
3) O gráfico a seguir mostra as posições
em função do tempo de dois ônibus. Um
ônibus parte de uma cidade A em direção a
uma cidade B, e o outro da cidade B para a
cidade A. As distâncias são medidas a
partir da cidade A. A que distância os dois
veículos vão se encontrar?
Adotaremos ônibus azul como A e ônibus
vermelho como B.
A função horária informa a posição do veículo em função do tempo decorrido. Assim
faremos a função horária para ambos os veículos.
Velocidade ônibus A =>
∆
=∆ =
= 90
/ℎ
SA= 0 + 90*T
Velocidade
ônibus
B
=>
∆
=∆ =
= −64,29
/ℎ
(o
veículo
está
se
movimentando contra a orientação – posição final = 0 e posição inicial = 450km.
∆ = 0 − 450 = −450
SB= 450 - 64,29*T
A posição do encontro dos veículos será a mesma para ambos, ou seja, SA = SB
Igualando as duas funções horárias temos:
90*T = 450 - 64,29*T => 90*T + 64,29*T = 450
154,29*T = 450
=> T = 450 / 154,29 = 2,91h
Assim, os veículos irão se encontrar após 2,91h do início do percurso. Para
sabermos a posição do encontro basta substituir o tempo de encontro na função
horária dos veículos. Assim temos:
SA= 0 + 90*T
=> SA= 90 * 2,91
SB= 450 - 64,29*T
=> aproximadamente SA= 262km
=> SB= 450 - 64,29 * 2,91 => aproximadamente 262km
4) Um carro, se desloca a uma
velocidade de 20m/s em um primeiro
momento, logo após passa a se deslocar
com velocidade igual a 40m/s, assim
como mostra o gráfico abaixo. Qual foi a
distância percorrida pelo carro?
Quando temos um exercício contendo gráfico podemos, em muitas vezes, resolvêlo utilizando apenas o gráfico.
Neste caso o exercício informa um gráfico: VELOCIDADE x TEMPO. Podemos
resolvê-lo de duas maneiras:
1º pela área do gráfico que nos dá a posição:
Fazendo a área do gráfico A e B teremos a distância percorrida pelo carro. Assim
temos:
Área A = 20 * 5 = 100
Área B = (15 -5) * 40 = 400
Área total = 100 + 400 = 500 metros percorrido.
2º pela equação da velocidade média (temos velocidades constantes em dois
intervalos). Velocidade média do primeiro intervalo = a 20 m/s e o tempo total do
primeiro intervalo = 5 segundos.
∆
= ∆ = ∆S= 20 * 5 = 100 metros.
Velocidade média do segundo intervalo = 40 m/s e o tempo total = 15 -5 = 10s
∆
= ∆ = ∆S= 40 * (15 – 5) = 400 metros.
Distância total percorrida pelo carro = 500 metros.
5) Dois trens partem simultaneamente de um mesmo local e percorrem a
mesma trajetória retilínea com velocidades, respectivamente, iguais a
300km/h e 250km/h. Há comunicação entre os dois trens se a distância
entre eles não ultrapassar 10km. Depois de quanto tempo após a saída os
trens perderão a comunicação via rádio?
Velocidade do primeiro trem = 300 km/h || S1 = S0 + V * T = S = 300 * T
Velocidade do segundo trem = 250km/h || S2 = S0 + V * T = S = 250 * T
Os trens perderão a comunicação quando a variação da posição deles for superior a
10 km, assim S1 – S2 = 10 km. Fazendo S1 – S2 temos:
300 * T – 250 * T = 10
=> 50 * T = 10 => T = 10/50 => T= 0,2 h.
Os trens perderão comunicação após 0,2 horas da partida de ambos.
Achamos a função horária que permite saber a posição do trem em qualquer
instante do movimento. Após isso, temos que a distância mínima dos dois trens
deve ser de 10 km, ou seja, a variação da posição dos trens deve ser de 10km.
Como queremos a variação da posição, basta efetuar a subtração do das posições
entre o primeiro trem e o segundo trem, assim teremos o tempo em que eles
alcançaram uma distância de 10 km entre suas posições e após isso perderão a
comunicação.