Tamanho da Terra - Departamento de Física

Introdução à Astronomia e à Astrofı́sica
Sobre Tamanho da Terra
Prof. Dr. Dietmar William Foryta
Departamento de Fı́sica, Universidade Federal do Paraná, Centro Politecnico, Caixa Postal 19044,
81531-990, Curitiba, Paraná, Brasil ∗
A tentativa de determinação do tamanho da Terra passa por várias atividades que
usualmente na são apresentadas, ma que possuem importância capital no desenvolvimento de uma linha de raciocı́nio cientı́fico. Este desenvolvimento é perfeitamente adequado em diversas das fases escolares. A partir das primeiras determinações também pode-se construir uma idéia de como o sistema de planetas se
organiza.
Keywords: Terra: Experimento de Erastotenes;
Terra: Tamanho;
Lua: Experimento de Aristarcus;
Lua: Tamanho e Distância;
Sol: Tamanho e Distância;
Sistema Solar: Modelo Heliocentrico Primitivo;
1
Qua a Forma da Terra? . . . . . . . . . . .
1
1. Qua a Forma da Terra?
2
A Terra é uma Esfera? . . . . . . . . . . .
3
3
O Tamanho da Terra . . . . . . . . . . . .
4
4
O Problema do Paralelismo dos Raios do Sol
5
5
O Tamanho e a Distância a Lua . . . . . .
6
A forma de uma bola ou de um lápis são completamente diferentes, assim quando questionamos o tamanho de algum objeto nós devemos
questionar primeiramente sua forma. Qual seria a forma da Terra? Hoje sabemos que a
forma da Terra é uma esfera. Como no passado pode-se imaginar isto?
6
O Tamanho e a Distância ao Sol . . . . . .
7
7
Modelo Primitivo do Sistema de Planetas .
9
O tamanho da Terra é usualmente tratado
como um simples exercı́cio da aplicação de
trigonometria na disciplina de Matemática.
Todavia o problema do tamanho da Terra é
muito mais rico em possibilidades didáticas se
adequadamente enfocado.
∗
Electronic
address:
[email protected];
URL: http://fisica.ufpr.br/foryta
Para podermos compreender a Natureza que
nos cerca devemos questiona-la sobre o que
ela o é. Observemos a nossa volta. Morros,
nuvens, céu... Comparemos corpos de diversas formas e imaginemo-nos habitando a superfı́cie destes corpos, qual seria nossa visão
do mundo que nos cerca?
Se habitarmos um mundo com forma de
uma banana e estivermos na sua parte interna poderiamos ver a outra extremidade de
nosso mundo. O que temos certeza que não
ocorre. Se habitassemos um mundo infinitamente plano, bastaria irmos cada vez mais
alto e poderiamos perceber que poderiamos
2
Figura 1 Exemplo de objetos, de diversas formas,
para comparar e questionar qual destas pode ser
adequada para a forma da Terra. O princı́pio capital é imaginar-se habitando a superfı́cie destes
objetos.
ver cidades cada vez mais longe.
Uma das dificuldades de nossas observações
está na existência de morros e florestas que
nos impedem a visão. Então desloquemo-nos
para o litoral e observemos o mar e aproveitemos a partida de um barco. A medida em que
este barco se afasta torna-se cada vez menor,
em aparência, e após um tempo ele é gradualmente “engolido” pelo mar. Caso estivessemos
no alto de uma árvore, também perceberiamos
tal fenômeno, mas este ocorreria algum tempo
após a observação deste por uma pessoa que
estivesse mais embaixo. O que isto significa?
Este fenômeno é o horizonte e é bem conhecido
desde a antiguidade. Ele mostra que a superfı́cie das águas não é plana do ponto de
vista da geometria. A superfı́cie das águas do
Introdução à Astronomia e à Astrofı́sica
Figura 2 Um possı́vel método de determinação
da forma da Terra pode ser obtida pelo uso
de pequenos barcos puxando cordas a partir de
um grande barco. Caso todas os comprimentos das cordas forem aproximadamente do mesmo
tamanho a curvatura local da Terra é a mesma
em todas as direções. Este resultado é somente
compatı́vel com algumas formas.
mar apresentam uma curvatura para baixo. Se
a curvatura for pequena, poderemos percebela facilmente, mas se for muito grande poderemos ter dificuldade em percebe-la. Como verificar, e mesmo medir, a curvatura da superfı́cie
das águas do mar?
Imaginemos tal tipo de experimento sendo executado com a tencologia disponı́vel na antiga
grécia, época em que foi pela primeira vez estimado o tamanho da Terra. Peguemos um
barco e naveguemos para uma distância em
que a costa não possa ser observada. Coloquemos um observador em um mastro efaçamos
avançar um pequeno barco arrastando uma
corda. Quando o barquinho desaparecer para
o observador do mastro, marquemos na corda
qual sua distância.
Curitiba, 11 de Agosto de 2003
Sobre o Tamanho da Terra
3
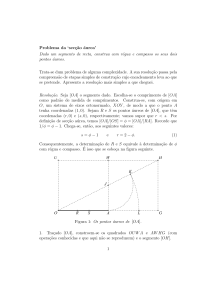
Raios Solares ¨Paralelos¨
Sienne
Poço
Alexandria
Sombra
Terra
Figura 3 A estimativa de erastotenes é aqui esquematizada. A distância entre as cidades de Alexandria
e Sienne de aproximadamente 800 km. A idéia básica é a existência de duas retas cruzadas por outra.
Este deve ser repetido várias vezes em direções
diferentes, pois há vários corpos que possuem
uma forma convexa, entre os diversos temos
esferas, ovos e pepinos. Se a distância medida até o desaparecimento, uma “medida” da
curvatura da Terra, for a mesma em todas as
direções poderemos descartar algumas das formas, ou posições dentro das formas. Quando
repetimos o experimento constatamos que em
todas as direções a distância é a mesma. Que
corpos podem ter tal tipo de resultado? Não
somente uma esfera, mas também poderemos
estar nas pontas de um ovo, ou de um pepino.
Como a possibilidade de estarmos justamente
na ponta da Terra em forma de ovo, ou pepino,
é pequena, então podemos acreditar que a
Terra é bem provavelmente uma esfera.
Claro que para termos, mais, certeza deveremos repetir o experimento deversas vezes em
lugares bem diferentes. Lugares conhecidos
por Dietmar William Foryta
pelos antigos gregos incluem o Golfo Pérsico,
o Mar da Arábia, o Mar Negro e todo o Mar
Mediterrâneo. Poder-se-iam mesmo fazer tal
experimento além das colunas de heracles (Estreito de Gilbraltar). Comparando-se os comprimentos da corda, constatariamos que todas
teriam a mesma distância. Isto implicaria que
a curvatura da Terra é a mesma em diversos
lugares distintos.
A forma do corpo que seria compatı́vel com tal
resultado seria somente uma esfera. E assim
passaremos a pensar que a Terra é uma esfera.
2. A Terra é uma Esfera?
O experimento do comprimento da corda no
mar indica que a forma da Terra é uma esfera,
mas seria a forma da Terra uma esfera?
Claro que não! Na Terra existem montanhas,
4
Introdução à Astronomia e à Astrofı́sica
Figura 4 Como o Sol não está a uma distância infinita, devido a propagação retilinea da luz implica
que os raios de luz do Sol não chegam paralelos a Terra. Todavia, se a distância for grande o suficiente,
a divergência dos raios do Sol serão pequenas o suficiente de maneira que sua não paralelidade possa
ser considerada desprezı́vel.
vales e diversas feiçoes geográficas em altitude.
Portanto a Terra não é uma esfera. E agora?
Peguemos uma bola qualquer, uma de basquete por exemplo, e olhemos-a atentamente.
Podemos perceber os “pontos” rugosos, a costura, eventuais arranhados e sulcos. Eles podem ser resumidos como altos e baixos para
uma formiga que está pela bola passeando.
Podemos interpretar estas diferenças de altura
como analogos às montanhas e vales. Apesar
de todas os possı́veis oscilações na superfı́cie
da bola, podemos olhar a bola como uma esfera. Por que não a Terra também? Somente
se tais montanhas sejam tão pequenas comparadas com o “tamanho” da esfera que podem ser consideradas como arranhões na sua
superfı́cie.
Esta análise inclui dois conceitos fundamentais na Ciência: abstração e modelagem.
A modelagem carcateriza-se por escolher alguma coisa que assemelha-se muito com aquilo
que se quer estudar mas que seja mais simples.
No caso da Terra, a Terra parece ser uma esfera, mesmo que saibamos que não o é.
A abstração caracteriza-se em eliminar de
nossa analise tudo que não é importante, ou
que não pareça importante, para a análise, por
exemplo a queda de objetos não depende da
cor da camisa da pessoa que está observando.
Em resumo a Terra, mesmo não sendo uma
esfera, pode ser imaginada, modelada, como
uma esfera.
3. O Tamanho da Terra
Erastotenes (276-194 a.C.) foi um dos mais
notáveis estudiosos do seu tempo e escreveu
sobre filosofia, sobre questões cientı́ficas e
literárias. Como matemático, Erastotenes inventou um método para encontrar números
primos. Sua reputação, entre seus contemporâneos, foi tão grande que Arquimedes dedicou um livro a ele. Como geógrafo, ele escreveu Geografia, o primeiro livro a dar a este
ramo do conhecimento uma base matemática
e tratar a Terra como um globo dividido em
zonas frigidas, temperadas e tórridas. Este
permaneceu como um trabalho padrão e foi
usado um século mais tarde por Júlio César.
Erastotenes permaneceu a maior parte de sua
vida em Alexandria e lá morreu em 194 a.C.
Sendo bibliotecário, seu segundo diretor, de
240 a 194 a.C., da Biblioteca de Alexandria,
Curitiba, 11 de Agosto de 2003
Sobre o Tamanho da Terra
5
Lua
Terra
Sol
Figura 5 A disposição da Terra, da Lua e do Sol pode ser estimada pelas observações. A Lua tem
sempre aproximadamente o mesmo tamanho com pouca variação, bem como o tamanho aparente do Sol,
o que significa que a distância destes a Terra não deve variam muito. Pelo conhecimento da existência
do eclipse solar podemos ter certeza que a distância do Sol a Terra é maior do que a distância da Lua
a Terra.
no Egito, cidade fundada por Alexandre, O
Grande, Erastotenes tinha o acesso a um volume considerável de informações. Entre elas,
sabia-se que no dia de Solistı́cio de Verão,
no hemisfério norte, no dia 22 de Junho de
cada ano, a luz do Sol era refletida diretamente pelo fundo de um poço d’água em Siene,
cidade diretamente ao Sul de Alexandria, onde
a represa de Aswan está atualmente. Isto significa que o Sol estava diretamente, verticalmente, sobre Siene.
erro menor do que 5%; surpreendente para a
época!
Assim, em 235 a.C., no dia de Solistı́cio, Erastotenes examinou a sombra de um monolito
vertical e determinou que esta tinha aproximadamente 1/8 da altura do monolito. Isto
corresponde a um ângulo de 7,2o , ou seja, 1/50
de um cı́rculo.
Pode-se experimentar a formação das sobras
de objetos iluminados pelo Sol e perceber que
a luz parece propagar-se retilineamente.
A distância entre as duas cidades era bem conhecida, já que existia um tráfego comercial
considerável, e foi medida por agrimensores da
época como 5000 estadia, ou 800 km (50 dias
de camelo, 16 km/dia).
Assim a Terra teria 42000 km de perimetro
ou 6700 km de raio. Estes valores contrastam com os atuais valores do perı́metro
é de 40200 km e 6370 km para o raio. Um
por Dietmar William Foryta
4. O Problema do Paralelismo dos Raios
do Sol
Uma idéia fundamental que está por trás desta
determinação é a presuposição de que os raios
do Sol sejam paralelos. Seria este paralelismo
correto?
O Sol, como fonte de luz, deve estar a uma
certa distância da Terra, assim, os raios de luz
do Sol partiriam do Sol e por consequência
divergeriam, não chegando paralelos a Terra.
Todavia a medida em que a distância entre o
local de observação e a fonte de lua crescer, os
raios de luz ainda chegarão não paralelos, mas
esta divergência seria cada vez menor. Se a
distância for grande o suficiente entre a Terra
e o Sol, então a divergência dos raios do Sol
poderão ser negligenciados.
Então fica pendente que a distância ao Sol
6
Introdução à Astronomia e à Astrofı́sica
Figura 6 Desde a antiguidade sabia-se que o movimento da Lua não descrevia um cı́rculo em torno
da Terra, então a Lua não era considerada um objeto “celeste” e, assim, deveria ser um fenômeno
atmosférico.
seja determinada para confirmar ou refutar a
aplicação geométrica feita por Erastotenes.
5. O Tamanho e a Distância a Lua
Um fenômeno surpreendente na Natureza é a
ocorrência de eclipses. Eles nos dão muitas informações sobre a localização dos objetos celestes que nos interessam, a Terra, a Lua e o
Sol. O mais surpreendente é o eclipse solar
pois ele evidência que o tamanho aparente do
Sol é aproximadamente o mesmo da Lua.
Pela ocorrência dos eclipses solares sabemos
que o Sol está mais distante do que a Lua.
Como os raios de luz percorrem uma trajetória retilı́nea, podemos associar o tamanho
do Sol a sua distância e o tamanho da Lua
e sua distância. Podemos extender este a
colocação de uma pequena moeda colocada a
frente da Lua e coloca-la a distância adequada
de maneira que seu disco cubra exatamente ao
da Lua. Assim sabendo qual a distância e o
tamanho da moeda, basta encontrar, seja o
tamanho, seja a distância, teremos o valor da
outra propriedade.
O eclipse solar também trás outra informação
interessante. Como o eclipse solar é rápido
comparado com a duração do dia, a extensão
da sombra na superfı́cie da Terra não deve ser
grande. Isto implica que o comprimento da
sombra da Lua é aproximadamente a distância
da Lua a Terra.
Analisemos também o eclipse lunar. O eclipse
lunar pode ser dividido em três fases, uma fase
de entrada na sombra da Terra, outra atravessando a sombra da Terra e outra emergindo
da sombra. Mesmo não sabendo do valor
numérico do tamanho da lua, podemos dizer
que a velocidade de entrada na sombra é de
um tamanho da lua no intervalo de tempo.
Bem provavelmente esta velocidade não deve
modificar durante a travessia da sombra. Assim, podemos medir a extensão da sombra da
Terra em tamanhos da Lua.
Sabendo que os tempos tı́picos destes eventos
são 4 minutos e 10 minutos, sabemos então
Curitiba, 11 de Agosto de 2003
Sobre o Tamanho da Terra
7
Eclipse Solar
Eclipse Lunar
fim do eclipse lunar
Terra
sombra da lua
lado do dia
lado da noite
inicio do eclipse lunar
Figura 7 Diagrama esquemático explicando o método utilizado para a determinação do tamanho da
Lua utilizando-se dos eclipses solares e lunares. O intervalo de tempo em que a Lua permanece completamente oculta na sombra da Terra é aproximadamente 2,5 para o intervalo de tempo para que a
Lua desapareça na sombra.
que a sobra da Terra é 2,5 vezes o tamanho da
Lua.
Terra. Basta encontrar um para saber outro.
Como encontrar algum destes?
É claro que o tamanho da sombra da Terra
não é o tamanho da Terra, mas associando
o fato de que a sombra do eclipse solar
toca a superfı́cie da Terra, podemos concluir
que a diminuição do tamanho da sombra do
tamanho da Terra até a posição de passagem
da Lua é de 1 tamanho da Lua, então podemos afirmar que a Terra é 3,5 vezes o tamanho
da Lua.
Quais informações já foram encontradas? Os
tamanhos da Terra e da Lua e a distância da
Terra a Lua.
Conhecido o tamanho da Terra, sabemos
então o tamanho da Lua. Sabendo o tamanho
da Lua, usando a moeda temos também a
distância da Terra a Lua. Ambos, supreendentemente, com um erro menor do que 5%
com os valores aceitos atualmente.
6. O Tamanho e a Distância ao Sol
A semelhança de tamanhos aparentes permite
vincular o tamanho do Sol com sua distância a
por Dietmar William Foryta
Como vamos associar três corpos, a Terra, a
Lua e o Sol, lembramos de um triangulo. Melhor ainda sabemos pelo menos uma distância,
da Terra a Lua. Falta-nos obter, seja dois
ângulos, seja um ângulo e uma distância para
obter todas as dimensões do triangulo.
Os gregos conheciam muito bem as propriedades dos triangulos retangulos, onde um
dos ângulos media 90o . Brincando com os triangulos possı́veis entre a Terra, a Lua e o Sol,
podemos associar um instante adequado em
que um ângulo de 90o entre as direções da Lua
a Terra e da Lua ao Sol. “Facilmente” podemos medir agora o ângulo entre a Terra e a
Lua e a Terra e o Sol.
Todavia a medida de ângulos próximos a 90o
era difı́cil para os gregos, onde a precisão
8
Introdução à Astronomia e à Astrofı́sica
Lua
angulo de 90 graus
angulo a ser
determinado
Terra
Sol
Figura 8 Um fenômeno perfeitamente visı́vel que ocorre com a Lua são as ditas fases da Lua. Em um
perı́odo conhecido como mês lunar, aproximadamente 28 dias, a feição clara da lua sai desde a completamente brilhante, a Lua Cheia, passa por uma fase em que diminui a área clara, a Minguante, atinge
um mı́nimo completamente escurecida, a Lua Nova, e a área clara volta a crescer, a Lua Crescente,
completando o ciclo na Lua Cheia.Para a determinação da distância ao Sol, quer-se obter um ângulo
de 90o entre as direções Terra-Lua e Lua-Sol, que é obtida quando a área clara está perfeitamente reta
no disco lunar. Observe que está imersa a idéia que a Lua é iluminada pelo Sol tal qual a Terra, que
a forma da Lua também é esférica.
era da ordem de 2,5o somente. Aristacus de
Samos mediu um ângulo de 87o estimando
uma distância ao Sol de 20 vezes maior do que
a da Terra a Lua.
Como a distância de 20 da Terra-Lua é consid-
eravelmente maior do que o tamanho da Terra,
os raios solares devem chegar com divergência
negligênciável.
O valor atualmente aceito é de 89,8o resultando em 400 vezes. Valor este que colabora
Curitiba, 11 de Agosto de 2003
Sobre o Tamanho da Terra
9
Venus
elongacao maxima
para Venus
Sol
Terra
Mercurio
Figura 9 Sabendo que Vênus e Mercúrio, objetos conhecidos pelos antigos gregos, nunca afastavam-se
muito do Sol, podemos imaginar que por analogia ao movimento da Lua, estes devem mover-se próximo
ao Sol, em torno do Sol.
ainda mais com o problema de paralelidade
dos raios solares.
7. Modelo Primitivo do Sistema de
Planetas
Aristarcus de Samus (310-230 a.C.) foi possivelmente o primeiro a sugerir que a Terra
apresenta um movimento de rotação diário e
por Dietmar William Foryta
que isto explicava o movimento das estrelas.
Ele tomou por hipótese que a Terra moviase em torno do Sol em uma órbita anual, e
que os outros planetas também o deveriam.
Ele mediu corretamente o diâmetro da Lua e
sua distância à Terra, em 240 a.C., dezesete
séculos antes que suas determinações fossem
completamente aceitas.
Quais outros objetos “celestes” podem ser estudados fora a Terra, a Lua e o Sol?
10
Existem as estrelas e as estrelas que não se
comportam como estrelas, as ditas estrelas errantes, estrelas que se movimentam quando
comparadas com as outras estrelas. Destas estrelas errantes duas chamam mais a atenção,
Mercúrio e Vênus. Estes nunca se afastam
muito do Sol. Vênus também é conhecida
como estrela vespertina ou matutina, pois é
mais facilmente percebida durante o amanhecer e no anoitecer.
Durante o movimento de Vênus podemos
localiza-lo a uma distância angular, e pode-
Introdução à Astronomia e à Astrofı́sica
mos determinar seu valor máximo. Três corpos, o Sol, a Terra e Vênus formam triângulos,
onde em instantes determinados poder-se-á ter
triangulos retangulos. Este instante coincide
com a elongação máxima. Como sabemos a
distância da Terra ao Sol, podemos determinar a distância entre Vênus e o Sol, supondo
que a trajetória deste seja circular.
O mesmo pode ser feito para Mercúrio e assim
podemos construir as posições tı́picas do sistema de corpos: Sol, Mercúrio, Vênus, Terra
e Lua.
Curitiba, 11 de Agosto de 2003