gabarito - Educacional

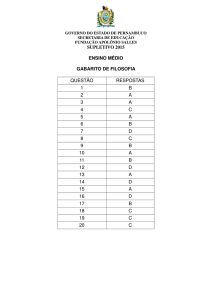
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
1) A figura abaixo representa um móvel m que descreve um movimento circular
uniforme de raio R, no sentido horário, com velocidade de módulo V.
Assinale a alternativa que melhor representa, respectivamente, os vetores velocidade V
e aceleração a do móvel quando passa pelo ponto I, assinalado na figura. (4,3 pontos)
a)
b)
c)
d)
e)
GABARITO [C]
No movimento circular uniforme (MCU) a velocidade é representada por um vetor
tangente ao círculo em cada ponto ocupado pelo móvel, com isto, apesar do módulo da
velocidade permanecer constante, ao longo do movimento o vetor velocidade altera sua
direção e sentido, sendo, portanto, um movimento acelerado em que a aceleração é
sempre perpendicular ao vetor velocidade apontando para o centro da curva, chamada
de aceleração centrípeta. Assim, a alternativa correta é a [C].
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
2) Vários corpos idênticos são abandonados de uma altura de 7,20m em relação ao
solo, em intervalos de tempos iguais. Quando o primeiro corpo atingir o solo, o quinto
corpo inicia seu movimento de queda livre. Desprezando a resistência do ar e adotando
a aceleração da gravidade g  10,0 m / s2, a velocidade do segundo corpo nessas
condições é (4,3 pontos)
a) 10,0 m / s
b) 6,0 m / s
c) 3,0 m / s
d) 9,0 m / s
e) 12,0 m / s
GABARITO: [D]
Calculando o tempo de queda:
h
1 2
g t q  tq 
2
2h

g
2  7,2 
10
 1,44  t q  1,2 s.
A figura mostra os cinco corpos e o tempo (t) de movimento de cada um deles.
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
A velocidade do 2º corpo é:
v  v 0  g t  v  0  10  0,9  
v  9 m/s.
3) O puma é um animal que alcança velocidade de até 18 m / s e pode caçar desde
roedores e coelhos até animais maiores como alces e veados. Considere um desses
animais que deseja saltar sobre sua presa, neste caso um pequeno coelho, conforme a
figura.
O puma chega ao ponto A com velocidade horizontal de 5 m / s e se lança para chegar à
presa que permanece imóvel no ponto B. Desconsiderando a resistência do ar e
adotando g  10 m / s2, a alternativa correta é: (4,4 pontos)
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
a) O puma não vai cair sobre a presa, pois vai tocar o solo a 20 cm antes da posição do
coelho.
b) O puma cairá exatamente sobre o coelho, alcançando sua presa.
c) O puma vai chegar ao solo, no nível do coelho, após 0,5 s do início de seu salto.
d) O puma vai cair 30 cm a frente do coelho, dando possibilidade da presa escapar.
GABARITO: [A]
O movimento do puma se jogando para pegar a presa é um lançamento horizontal.
Desta forma, pode-se dizer que o tempo de movimento é igual ao tempo de queda.
Como a velocidade inicial no eixo vertical ( v oy ) é nula, temos que:
S  So  v oy  t 
1,8 
a  t2
2
10  t 2
2
t 2  0,36
t  0,6 s
Assim, o deslocamento horizontal do puma é de:
ΔS  v x  t
ΔS  5  0,6
ΔS  3 m
Em posse desse deslocamento, é fácil notar que a resposta é a alternativa [A].
4) Dois corpos, um de massa m e outro de massa 5m, estão conectados entre si por um
fio e o conjunto encontra-se originalmente em repouso, suspenso por uma linha presa a
uma haste, como mostra a figura. A linha que prende o conjunto à haste é queimada e o
conjunto cai em queda livre.
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
Desprezando os efeitos da resistência do ar, indique a figura que representa
corretamente as forças f1 e f2 que o fio faz sobre os corpos de massa m e 5m,
respectivamente, durante a queda. (4,4 pontos)
a)
b)
c)
d)
e)
GABARITO: [E]
Corpos em queda livre não trocam forças entre si, pois caem com a mesma aceleração
que é igual à aceleração da gravidade.
Desenhando as forças que atuam nos corpos em queda livre:
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
Como a única força que atua nos corpos é a força peso, podemos dizer que: FR  P , onde
FR representa a força resultante que atua nos corpos (não se esqueça de que FR  m.a e
P  m.g ).
Corpo de massa m: FR  P  m.a  m.g  a  g
Corpo de massa 5m: F'R  P'  5m.a'  5m.g  a'  g
Ou seja: a  a'  g
5) Um lançador de granadas deve ser posicionado a uma distância D da linha vertical
que passa por um ponto A. Este ponto está localizado em uma montanha a 300 m de
altura em relação à extremidade de saída da granada, conforme o desenho abaixo.
A velocidade da granada, ao sair do lançador, é de 100 m s e forma um ângulo “α ” com
a horizontal; a aceleração da gravidade é igual a 10 m s2 e todos os atritos são
desprezíveis. Para que a granada atinja o ponto A, somente após a sua passagem pelo
ponto de maior altura possível de ser atingido por ela, a distância D deve ser de: (4,4
pontos)
Dados: Cos α  0,6; Sen α  0,8.
a) 240 m
b) 360 m
c) 480 m
d) 600 m
e) 960 m
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
GABARITO: [D]
Decompondo a velocidade em componentes horizontal e vertical, temos:

 Vx  V0 .cos α  100x0,6  60 m/s


 Vy  V0 .senα  100x0,8  80 m/s
Na vertical o movimento é uniformemente variado. Sendo assim:
1
ΔSy  Vy .t  gt 2  300  80t  5t 2  t 2  16t  60  0
2
A equação acima tem duas soluções: t= 6s e t’=10s.
Como o projétil já passou pelo ponto mais alto, devemos considerar o maior tempo
(10s).
Na horizontal, o movimento é uniforme. Sendo assim:
ΔSx  Vx .t  D  60x10  600m
6) Um balão dirigível sobe verticalmente, com velocidade constante de 90,0 km h em
relação ao solo, e, a uma altura de 80,0 m do chão, um de seus passageiros arremessa
um objeto com velocidade vertical e para cima de 18,0 km h, em relação ao piso do
cesto do balão. Em quantos segundos, o objeto retorna para a mão do passageiro? (4,4
pontos)
GABARITO:
1ª opção:
Ajustando as velocidades em relação ao solo no Sistema Internacional de Unidades:
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
Balão: vb  90 km / h 
1m / s
 25 m / s
3,6 km / h
Objeto: v0  18  90  km / h 
1m / s
 30 m / s
3,6 km / h
Tomando as velocidades em relação ao solo, as equações das posições dos móveis em
relação ao tempo são:
Balão: h  80  25t (1)
Objeto: h  80  30t  5t 2 (2)
Para que o objeto retorne à mão do passageiro é necessário que a posição indicada
pelo balão seja a mesma do objeto, portanto, fazendo a igualdade das duas equações:
80  25t  80  30t  5t 2
25t  30t  5t 2
5t 2  5t  0
t2  t  0
t   t  1  0
Resolvendo a equação de segundo grau incompleta, as raízes são:
t '  0 s e t ''  1 s.
Logo, após o lançamento, o objeto retorna ao passageiro em apenas 1 segundo.
2ª opção:
Considerando o balão como um sistema inercial, usamos somente a informação do
objeto efetuando um lançamento vertical com velocidade inicial referida ao balão.
Objeto: v0  18 km / h 
1m / s
5 m/s
3,6 km / h
Usando a equação horária da velocidade para o lançamento vertical, v  v0  gt.
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
Sabendo-se que a velocidade final terá sentido contrário da velocidade inicial, mas de
mesmo módulo e usando a aceleração da gravidade g  10 m / s2 :
5  5  10t  t  1 s
7) Em um dia de calmaria, um garoto sobre uma ponte deixa cair, verticalmente e a
partir do repouso, uma bola no instante t0 = 0 s. A bola atinge, no instante t4, um ponto
localizado no nível das águas do rio e à distância h do ponto de lançamento. A figura
apresenta, fora de escala, cinco posições da bola, relativas aos instantes t0, t1, t2, t3 e t4.
Sabe-se que entre os instantes t2 e t3 a bola percorre 6,25 m e que g = 10 m/s2.
Desprezando a resistência do ar e sabendo que o intervalo de tempo entre duas posições
consecutivas apresentadas na figura é sempre o mesmo, calcule a distância h, em
metros. (4,4 pontos)
GABARITO:
Analisando a figura, se o intervalo de tempo  Δt  entre duas posições consecutivas
quaisquer é o mesmo, então:
t2  2 t; t3  3 t e t3  4 t.
Aplicando a função horária do espaço para a queda livre até cada um desses instantes:
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
S
1
g t2
2
S  5 t 2
2
 2

2

S3  5 t3
 S
1
10  t 2
2
 S  5 t 2.
 S2  5  2 Δt 
2
 S2  20 Δt 2
 S3  5  3 Δt 
2
2
 S3  45 Δt
 S3  S2  25 Δt 2  6,25  25 Δt 2 
Δt 2  0,25.
Aplicando a mesma expressão para toda a queda:
h  5 t 24
 h  5  4 Δt 
2
 h  80 Δt 2  80 0,25  
h  20 m.
8) Durante um jogo de futebol, um goleiro chuta uma bola fazendo um ângulo de 30
com relação ao solo horizontal. Durante a trajetória, a bola alcança uma altura máxima
de 5,0 m. Considerando que o ar não interfere no movimento da bola, qual a velocidade
que a bola adquiriu logo após sair do contato do pé do goleiro? (4,4 pontos)
GABARITO:
Sabendo que na posição da altura máxima a componente vertical da velocidade é zero,
utilizando a equação de Torricelli, podemos dizer que:
GABARITO DA AFE02 – FÍSICA – 2ª SÉRIE – 2016
v y 2  v oy 2  2  a  ΔS
0  v oy 2  2  g  Hmáx
v oy 2  2  10  5
v oy  100
v oy  10 m s
Note que a aceleração neste movimento é em módulo igual a aceleração da gravidade.
Porém, a  g, devido a aceleração da gravidade, no movimento analisado, está contra o
movimento.
Sabendo que o ângulo de lançamento da bola é de 30C, podemos encontrar a
velocidade inicial da bola.
v oy  v o  sen  30 
v oy
10
vo 

sen  30  1 2
v o  20 m s