PDF_Aula 1 _ Conjuntos - Professor Luciano Nóbrega

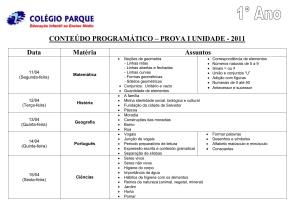
1
ÁLGEBRA
AULA 1 _ Conjuntos
Professor Luciano Nóbrega
Maria Auxiliadora
2
Teoria dos Conjuntos
Pode-se dizer que a Teoria dos Conjuntos é, em
grande parte, trabalho de um único matemático:
Georg Cantor (1845-1918).
A noção de conjunto não é suscetível de definição
precisa a partir de noções mais simples, ou seja, é
uma noção primitiva.
A Teoria dos Conjuntos é de fundamental importância
para várias áreas da ciência da computação.
CONCEITOS PRIMITIVOS
1º) Conjuntos – Um conjunto é uma coleção não-ordenada de
objetos. USAMOS LETRAS MAIÚSCULAS PARA REPRESNTÁ-LOS.
Exemplos:
• Conjunto de livros na biblioteca (conj. finito);
• Conjunto dos números naturais (conj. infinito);
• Conjunto de dinossauros vivos (conj. vazio, {}, Ø).
3
Teoria dos Conjuntos
CONCEITOS PRIMITIVOS
2º) Elementos – Os objetos que constituem um conjunto
denominam-se elementos do conjunto.
*usamos letras minúsculas.
Exemplos:
Eu, sou um elemento do conjunto de Matemáticos;
“1” é um elemento do conjunto dos Números Naturais.
“-2” é elemento do conjunto solução da equação x2 – 4 = 0.
3º) Pertinência – Notação: ∈ (pertence) ou ∉ (não pertence)
Qualquer objeto que seja elemento de um conjunto é
dito pertencer aquele conjunto.
LEMBRE-SE: A relação de pertinência, ∈ ou ∉ , é utilizada
somente para relacionar elementos com conjuntos.
4
Teoria dos Conjuntos
CONCEITOS PRIMITIVOS
4º) Continência – Notação: ⊂ (contido) ou ⊄ (não está contido)
Quando um conjunto estiver inserido em outro conjunto,
dizemos que o primeiro conjunto está contido no segundo
conjunto.
LEMBRE-SE: A relação de continência, ⊂ ou ⊄, é utilizada somente
para relacionar conjunto com conjunto.
Exemplo: Utilize, corretamente, um dos quatro símbolos:
a) 4/11 ___ N
b) N ___ Ir
c) N ___ R
d) √5 ___ R
e) -4,7 ___ Z
5º) Conjunto Universo – Notação: U
Chama-se Conjunto Universo a todos os entes que são
considerados como elementos.
Exemplo: em geometria o Universo é o conjunto de todos os
pontos.
5
Teoria dos Conjuntos
CARACTERÍSTICAS DOS CONJUNTOS
A ordem em que os elementos são listados e a repetição dos
elementos em um conjunto é irrelevante. Sendo assim:
{3, 2, 1} = {1, 2, 3}
e
{1, 1, 1, 3, 2, 2} = {1, 2, 3}
MANEIRAS DE DESCREVER UM CONJUNTO
– De maneira explícita. Ex: A = {água, terra, fogo, ar}
– Indicando um padrão: Ex: P = {2, 4, 6, 8, ...}
– Através de uma propriedade que os elementos do
conjunto tenham em comum. Ex: L = {x|x é um inteiro e 3 < x < 7}
– Através de um Diagrama de Venn.
– Com a notação de intervalos.
Ex: [3, 7] ; ] –9, 0 [
fechado
aberto
6
Teoria dos Conjuntos
CONJUNTOS ESPECIAIS – Os conjuntos numéricos
N: conjunto dos números naturais: {0, 1, 2, 3, ...}
Z: conjunto dos números inteiros: {..., -2, -1, 0, 1, 2, ...}
Q: conjunto dos números racionais: {x|x = a/b ; a, b ∈ Z , b ≠ 0}
I: conjunto dos números irracionais: {x|x ∉ Q}
R: conjunto dos nos reais: {x | x ∈ (Q ⋃ I)}
OPERAÇÕES COM CONJUNTOS
Para facilitar o entendimento, sejam os conjuntos: A = {1, 2, 3, 4} e B = {3, 4, 5, 6}.
UNIÃO: Se “A” e “B” são conjuntos, a união de “A” e “B”, denotada
por A ⋃ B, é o conjunto que contém aqueles elementos que estão
em “A”, ou em “B”, ou em ambos.
Ex: A ⋃ B = {1, 2, 3, 4, 5, 6}
INTERSEÇÃO: Se “A” e “B” são conjuntos, a
interseção de “A” e “B”, denotada por A ⋂ B, é o
conjunto que contém aqueles elementos que estão
em “A” e em “B” ao mesmo tempo.Ex: A ⋂ B = {3, 4}
7
Teoria dos Conjuntos
OPERAÇÕES COM CONJUNTOS
Para facilitar o entendimento, sejam os conjuntos: A = {1, 2, 3, 4} e B = {3, 4, 5, 6}.
DIFERENÇA:
Se “A” e “B” são conjuntos, a diferença de “A” e “B”, denotada
por A – B, é o conjunto que contém aqueles elementos que
estão em “A” mas não estão em “B”.
Ex: A – B = {1, 2} ; B – A = {5, 6}
COMPLEMENTO:
Se “U” é o conjunto Universo, U – A é chamado
de complemento de “A” e é denotado por “ Ā ”.
Ex: Ā = U – A = {5, 6}
PRODUTO CARTESIANO:
O produto cartesiano de dois conjuntos é o conjunto de todos
os pares ordenados dos elementos do primeiro conjunto que
pode-se formar com os elementos do segundo conjunto.
Ex: A x B = {(1,3);(1,4);(1,5);(1,6); (2,3);(2,4);(2,5);(2,6);
(3,3);(3,4);(3,5);(3,6); (4,3);(4,4);(4,5);(4,6)}
8
Teoria dos Conjuntos
OPERAÇÕES COM CONJUNTOS
Igualdade de Conjuntos:
Dois conjuntos “A” e “B” são iguais quando todo
elemento de “A” pertence também a “B” e,
reciprocamente, todo elemento de “B” pertencer à “A”.
Subconjuntos:
Quando todos os elementos de um conjunto “A” pertencem a
um outro conjunto “B”, diz-se, então, que “A” é um
OBS 1: O
número de
subconjunto de “B”, ou seja A ⊂ B.
elementos de
Observações:
P(A) é dado
• Todo o conjunto “A” é subconjunto dele próprio;
por 2n , onde
• O conjunto vazio é subconjunto de qualquer conjunto.“n” é o
número de
Ex: Seja o conjunto A = {1, 2, 3, 4}, então todos os
elementos de
subconjuntos de “A” são:
“A”.
P(A) = ( {1}; {2}; {3}; {4}; {1, 2}; {1, 3}; {1, 4}; {2, 3}; {2, 4}; {3, 4}; OBS 2:
N Z Q R
{1, 2, 3}; {1, 2, 4}; {1, 3, 4}; {2, 3, 4}; A; Ø})
9
Teoria dos Conjuntos
NÚMERO DE ELEMENTOS DA REUNIÃO DE CONJUNTOS
Consideremos o conjunto “A” como o conjunto dos números
ímpares entre 0 e 10, e o conjunto “B” dos números primos
entre 0 e 10. Então, se n(A) representa a quantidade de
elementos do conjunto “A”, temos:
A = {1, 3, 5, 7, 9}
n(A) = 5
n(A) = 4
B = {2, 3, 5, 7}
Vejamos o que acontece quando estudamos a interseção e a
união dos conjuntos:
n(A ⋃ B) = 6
A ⋃ B = {1, 2, 3, 5, 7, 9}
n(A ⋂ B) = 3
A ⋂ B = {3, 5, 7}
Observe que n(A ⋃ B) ≠ n(A) + n(B). Na verdade, temos:
n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)
6
= 5 + 4 – 3
10
Teoria dos Conjuntos
NÚMERO DE ELEMENTOS DA REUNIÃO DE CONJUNTOS
É possível provar que n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B), vejamos:
2º) Algebricamente:
n(A ⋃ B) = [n(A) – n(A ⋂ B)] + n(A ⋂ B) + [n(B) – n(A ⋂ B)]
n(A ⋃ B) = n(A) – n(A ⋂ B) + n(A ⋂ B) + n(B) – n(A ⋂ B)
n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)
1º) Geometricamente:
A
B
A
B
+
AUB
–
n(A ⋃ B ⋃ C) = n(A) + n(B) + n(C)
– n(A ⋂ B) – n(A ⋂ C) – n(B ⋂ C)
+ n(A ⋂ B ⋂C)
Resumo
11
n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)
O número de elementos de P(A) é
dado por 2n , onde “n” é o número
de elementos de “A”.
2n ( A )
Generalizando:
2
n (P(P(P(...(P(A)...))))  2 2
LEMBRE-SE: A relação de
pertinência, ∈ ou ∉ , é utilizada
somente para relacionar
elementos com conjuntos.
LEMBRE-SE: A relação de
continência, ⊂ ou ⊄, é utilizada
somente para relacionar conjunto
com conjunto.
PROPRIEDADES:
P1: A   = 
P2: A  B = B  A
P3: (A  B)  C = A  (B  C)
P4: A  A = A
P5: A   = A
P6: A  B = B  A
P7: (A  B)  C = A  (B  C)
OBS: Como foi dito na nossa preleção, minhas aulas terão vários exercícios resolvidos e
outros tantos à resolver. Nesta aula, não tivemos nenhum exercício resolvido pelo fato de
vocês já estarem de posse de uma lista com uns 50 exercícios.
TESTANDO OS CONHECIMENTOS
1 – (lista_questão 1) – Seja o conjunto A = {1, 2, 3, {3}, {4}, {2, 5}}.
Classifique as afirmações em verdadeiras (V) ou falsas (F).
a) 2  A
h)   A
b) {2}  A
i) {3}  A
c) 3  A
j) {4}  A
d) {3}  A
k) {{4}}  A
e)   A
l) {2, 5}  A
f) {5}  A
m) {{2, 5}}  A
g) {2, 5}  A
n) {1, 2, 3}  A
12
13
TESTANDO OS CONHECIMENTOS
2 – (lista_questão 4) – (Cesgranrio – RJ) O número de conjuntos X que
satisfazem {1, 2}  {1, 2, 3, 4} é:
a) 3
b) 4
c) 5
d) 6
3 – (lista_questão 7) – Sejam A = {x  /x é número par compreendido
entre 3 e 15}, B = {x  /x é um número par menor que 15} e C = {x  /x é
um número par diferente de 2}. Usando os símbolos  ou , relacione entre si
os conjuntos:
a) A e B
b) A e C
c) B e C
14
TESTANDO OS CONHECIMENTOS
4 – (lista_questão 10) – (Unifor – CE) Se A = {a, 3, }, então o número de
elementos de P(P(A)) possui:
a) 8 elementos
b) 16 elementos
c) 256 elementos
d) 512 elementos
5 – (lista_questão 16) – Numa pesquisa sobre a preferência em relação a
dois jornais, foram consultadas 630 pessoas e o resultado foi o seguinte: 350
delas lêem o jornal A, 210 lêem o jornal B e 90 lêem os jornais A e B.
Pergunta-se:
a) quantas pessoas lêem apenas o jornal A?
b) quantas pessoas lêem apenas o jornal B?
c) quantas pessoas lêem jornais?
d) quantas pessoas não lêem jornais?
15
TESTANDO OS CONHECIMENTOS
6 – (lista_questão 19) – Numa escola mista existem 42 meninas, 24 crianças
ruivas, 13 meninos são ruivos e 9 meninas ruivas. Pergunta-se:
a) Quantas crianças existem na escola?
b) Quantas crianças são meninas ou são ruivas?
7 – (lista_questão 21) – O quadro abaixo mostra o
resultado de uma pesquisa sobre as revistas que os
estudantes do Ensino Médio costumam ler:
Revistas
Leitores
Pergunta-se:
A
150
a) Quantos foram os estudantes consultados?
B
200
C
250
Ae B
70
Ae C
90
BeC
80
A, B e C
60
Nenhuma
180
b) Quantos estudantes lêem
apenas a revista A?
c) Quantos estudantes lêem a
revista B e não lêem a C?
d) Quantos estudantes não lêem
a revista A?
e) Quantos estudantes lêem a
revista A ou a revista C?
16
TESTANDO OS CONHECIMENTOS
8 – (lista_questão 27) – (UFRN) Indique a opção sempre verdadeira,
quaisquer que sejam os conjuntos A, B e C, de modo que A  B.
a) A  B  C
b) A  C  
c) B  C  
d) A  C  B
9 – (lista_questão 32) – (UFRN) As figuras abaixo representam diagramas
de Venn dos conjuntos X, Y e Z. Marque a opção em que a região hachurada
representa o conjunto Y  Z – X.
10 – (lista_questão 35) – (UFRN) Se A, B e C são
conjuntos tais que n[A – (B  C)] = 15, n[B – (A 
C)] = 20,
n[C – (A  B)] = 35 e n(A  B  C) =
120. Então n[(A  B)  (A  C)  (B  C)] é igual a:
a) 40
b) 50
c) 60
d) 70
11 – (lista_questão 37) – (UFRN) Uma pesquisa de opinião, realizada num
bairro de Natal, apresentou o resultado seguinte: 65% dos entrevistados
freqüentavam a praia de Ponta Negra, 55% freqüentavam a praia do Meio e 15%
não iam a praia. De acordo com essa pesquisa, o percentual dos entrevistados que
freqüentavam ambas as praias era de: a) 20% b) 35% c) 40% d) 25%